『量子論理の限界』について ( IV )
- 形而上学(あるいは超‐物理学) (Meta-physics)
- 自然哲学者のための量子力学 ( I ) (Quantum mechanics for natural philosophers ( I ))
- 波動‐粒子の2重性 (Wave-particle duality)
- コペンハーゲン解釈 ( I ) (The Copenhagen interpretation ( I ))
- コペンハーゲン解釈 ( II ) (The Copenhagen interpretation ( II ))
- 自然哲学者のための量子力学 ( II ) (Quantum mechanics for natural philosophers ( II ))
- 射影公準 (Projection postulates)
- 非局所性と隠れた変数 (Nonlocality and hidden variables)
- 使い勝手の量子論理 (A user-friendly quantum logic)
- 量子論理 (Quantum logic: what it can and can't do)
まず、Σ を適当な記号からなる可算無限集合として、Σ の要素を文記号と呼ぶことにする。(論理の形式系は汎用であるべきだから、ELQM の基本文のような具体的な文を所与の素材とする訳にはいかない。そこで、基本文のダミーとして文記号を用いる訳だ。)文記号と論理結合子「¬」、「∧」、「∨」、「⇒」、そして区切り記号としての括弧「 ( 」、「 ) 」が NDQL の基本記号だ。
通常の文に相当するのは、基本記号を適宜組み合わせて得られる記号列だ。それらを「式」と呼ぶ。式は次のように帰納的に定義することができる。
- 文記号は式である。
- φ が式ならば ¬φ は式である。(つまり、式に「¬」を接頭したものもまた式である。)
- φ と ψ が式ならば (φ ∧ ψ ) は式である。(つまり、式と式を「∧」で接続し括弧でくくったものもまた式である。)
- φ と ψ が式ならば (φ ∨ ψ ) は式である。
- φ と ψ が式ならば (φ ⇒ ψ ) は式である。
- 以上によって得られるものだけが式である。
有限箇の式からなる(空であり得る)集合とひとつの式の順序対をゼクヴェンツと云う。(「ゼクヴェンツ」はドイツ語の「Sequenz」の音訳。この語は、もともと、ゲンツェンによって、式の有限列の順序対を表わすのに用いられたものだそうで、英語では、「sequence」が列を意味するため、「sequent」が当てられている。)ゼクヴェンツの第一の要素(つまり式の集合)を前提と云い、第二の要素を帰結と云う。
以下では、式を「φ」等のギリシア小文字で表わし、有限箇の式からなる(空であり得る)集合を「Γ」等の大文字で表わす。特に空集合は「{ }」で表わす。このような、形式系の記号列等を代表する記号をメタ記号と云う。論理結合子および括弧に対しては、それら自体をメタ記号として流用する。また、前提 Γ と帰結 φ をもつゼクヴェンツを「Γ├ φ」と表わす。こうしたメタ記号からなる表現をスキーマと云う。(先の式の定義もスキーマに依っていた訳だ。)
厳格な形式化は徒にことを煩瑣にしてしまうので、略式で行くことにすれば、NDQL の公理と推論規則は、スキーマを用いて次のように表わせる。
| A (公理スキーマ) |
|
|||||||||||||||||
| MP (モドゥス・ポネンス) |
Γ ∪Δ├ ψ |
|||||||||||||||||
| MT (モドゥス・トレンス) |
Γ ∪Δ├ ¬φ |
|||||||||||||||||
| DN (二重否定) |
|
|||||||||||||||||
| ∧I (∧導入) |
Γ ∪Δ├ (φ ∧ ψ ) |
|||||||||||||||||
| ∧E (∧除去) |
|
|||||||||||||||||
| ∨I (∨導入) |
|
|||||||||||||||||
| ∨E (∨除去) |
Γ├ χ |
|||||||||||||||||
| CP (条件化) |
{ }├ (φ ⇒ ψ ) |
|||||||||||||||||
| RAA (帰謬法) |
{ }├ ¬φ |
|||||||||||||||||
| D1 (定義 1) |
|
|||||||||||||||||
| D2 (定義 2) |
|
| ∨ES (標準的∨除去) |
Γ ∪ (Δ - {φ }) ∪ (Θ - {ψ })├ χ |
||||||||||||||||
| CPS (標準的条件化) |
Γ - {φ }├ (φ ⇒ ψ ) |
||||||||||||||||
| RAAS (標準的帰謬法) |
Γ - {φ }├ ¬φ |
||||||||||||||||
| ¬E (否定除去) |
Γ├ ψ |
|
Γ├ (¬φ ∨ (φ ∧ ψ )) |
Γ├ (φ ⇒ ψ ) |
NDQL における証明は、公理を推論規則と定義 1 に従って変換していく有限のステップの有限の組み合わせからなる。形式的には、証明は、ゼクヴェンツによってラベル付けられた特殊なツリーとして規定できる。その葉のラベルは何れも公理で、ラベルの間には推論規則と定義 1 に則った関係が在って、それが対応する節の間の関係と同型になっているような有限ツリーだ。そうしたツリーを証明ツリーと云う。Γ├ φ を根のラベルとしてもつ証明ツリーが在るとき、Γ├ φ は証明可能であると云われ、{ }├ φ が証明可能なとき、 φ は証明可能であると云われる。
証明ツリーを図式化すれば証明図が得られる。また、公理スキーマや推論規則を、個別のゼクヴェンツではなく、ゼクヴェンツのスキーマに適用した証明図を考えることもできる。例えば、排中律スキーマ「(φ ∨ ¬φ )」の証明図は次のようになる。(なお、以下では、式のスキーマの外側の括弧は省くことにする。)
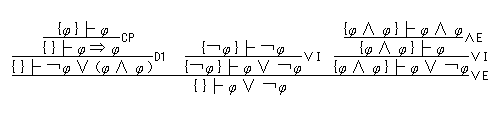
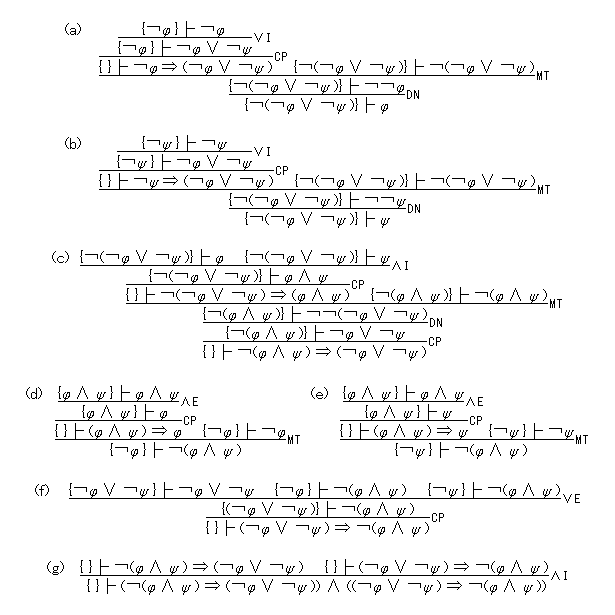
|
Γ├ ¬φ ∨ ¬ψ |
Γ├ ¬(φ ∧ ψ ) |
次はNDQL の意味論だ。ギビンズはそれをきちんと提示していないが、おおよそのことは示唆されているので、それをもとに、以下にひとつの意味論を定式化してみる。
量子命題論理の意味論のためには、(古典命題論理の場合と違って)真理値表は役にたたないので、別の道具が要る。そのひとつが直モジュラ束だ。
はじめに、NDQL では、{φ, ψ }├ χ が証明可能なことと {φ ∧ ψ }├ χ が証明可能なことは同等であり、また、{φ }├ ψ が証明可能なことと φ ⇒ ψ が証明可能なことと ((φ ∧ ψ ) ⇒ φ ) ∧ (φ ⇒ (φ ∧ ψ )) が証明可能なことは同等である一方、直モジュラ束 Ω においては、a ≦ b となることと a⊥∨Ω (a ∧Ωb ) = 1 となることは同等であることを示しておく。
まず、{φ, ψ }├ χ が証明可能だとすれば、証明ツリーの葉は何れも公理であり、その前提はひとつの式しかもたない訳だから、前提 {φ } をもつゼクヴェンツと前提 {ψ } をもつゼクヴェンツが MP か MT か ∧I の何れかによって前提 {φ, ψ } をもつゼクヴェンツに変換されるステップが在ることになる。それが、例えば、
{φ }├ α ⇒ β {ψ }├ α
{φ, ψ }├ β
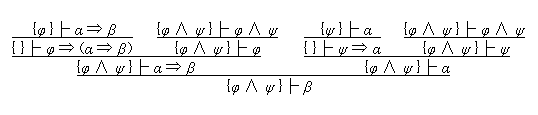
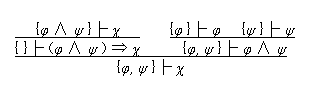
a⊥∨Ω (a ∧Ωb ) = a⊥∨Ω a = 1
逆に、a⊥∨Ω (a ∧Ωb ) = 1 とすれば、(7)と ∧Ω の属性からa ∧Ω(a⊥∨Ω (a ∧Ωb )) = a ∧Ω1 = a
一方、束の属性(1)から a ∧Ωb ≦ a、また、反射律から a⊥≦ a⊥、したがって、直モジュラ律によりa ∧Ω(a⊥∨Ω (a ∧Ωb )) = a ∧Ωb
よって、a ∧Ωb = a、したがって、(2)から a ≦ b。(直モジュラ律は、第六章において、c ≦ a かつ b ≦ a⊥ならば、a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
として定式化されていたが、b ≦ a⊥ならば、∧ の属性から b ∧ a⊥= b、よって、結合律と交換律そして(10)と(8)からb ≦ a⊥ならば a ∧ b = a ∧ (b ∧ a⊥) = b ∧ (a ∧ a⊥) = b ∧ 0 = 0
また、c ≦ a ならば a ∧ c = c、よって、∨ の属性からc ≦ a かつ b ≦ a⊥ならば、(a ∧ b ) ∨ (a ∧ c ) = 0 ∨ c = c
したがって、直モジュラ律は、c ≦ a かつ b ≦ a⊥ならば、a ∧ (b ∨ c ) = c
として定式化することもできる。)そこで、f を文記号全体の集合 Σ から直モジュラ束 Ω への写像として、式全体の集合 Φ から Ω への写像 Jf を次のように定義する。
- φ が文記号ならば Jf (φ ) = f (φ )
- Jf (¬φ ) = Jf (φ )⊥
- Jf (φ ∧ ψ ) = Jf (φ ) ∧ΩJf (ψ )
- Jf (φ ∨ ψ ) = Jf (φ ) ∨ΩJf (ψ )
- Jf (φ ⇒ ψ ) = Jf (¬φ ∨ (φ ∧ ψ ))
φ が恒真であるとは、どんな直モジュラ束 Ω および Ω への解釈 J についても J (φ ) = 1 となることを云う。また、ゼクヴェンツの恒真性を次のように定義する。
空でない前提をもつゼクヴェンツ {φ1, . . . , φn }├ ψ が恒真であるとは、どんな直モジュラ束 Ω および Ω への解釈 J についても J (( . . . (φ1∧φ2) ∧ . . . ) ∧ φn ) ≦ J (ψ ) となることを云い、空な前提をもつゼクヴェンツ { }├ φ が恒真であるとは φ が恒真であることを云う。(これらの定義が整合的なことは、先に示しておいたことがらから判る。)
ちなみに、古典命題論理の形式系に関しても、直モジュラ束の替わりにブール束を採れば、上と同様に意味論が展開できるが、その場合には、しかし、式 φ の恒真性は、1 と 0 だけを要素としてもつブール束 B2 へのどんな解釈 J についても J (φ ) = 1 となることに還元できる。これは、古典命題論理が真理値表だけですっかり規定できてしまうことに対応している。(否定および連言と選言についての真理値表は B2 の直補演算および交わりと結びの演算を規定する表と同型だ。)
一般に、論理の形式系は、それにおいて証明可能な式が凡て恒真であるとき健全であると云われ、恒真な式が凡て証明可能であるとき完全であると云われる。NDQL は健全かつ完全だ。健全性は、公理の恒真性および凡ての推論規則が恒真性を保存することを示すことによって証明できる。例として、MT をとってみれば次のようになる。
ゼクヴェンツの前提がひとつの式からなる場合を考えれば十分だから、{α }├ φ ⇒ ψ と {β }├ ¬ψ が恒真、つまり、J を任意の解釈として次が成り立つとする。
J (α ) ≦ J (φ )⊥∨Ω (J (φ ) ∧ΩJ (ψ )), J (β ) ≦ J (ψ )⊥
すると、第六章に示されている束の属性(1)、(2)、(5)から
J (α ) ∧ΩJ (β ) ≦ J (α ) ≦ J (φ )⊥∨Ω (J (φ ) ∧ΩJ (ψ ))
J (α ) ∧ΩJ (β ) ≦ J (β ) ≦ J (φ )⊥∨ΩJ (ψ )⊥
J (α ) ∧ΩJ (β ) ≦ (J (φ )⊥∨ΩJ (ψ )⊥) ∧Ω(J (φ )⊥∨Ω (J (φ ) ∧ΩJ (ψ )))
ところが、J (φ ) ∧ΩJ (ψ ) ≦ J (φ ) から、直相補束の属性(11)により、J (φ )⊥≦ (J (φ ) ∧ΩJ (ψ ))⊥、同様に、J (φ ) ∧ΩJ (ψ ) ≦ J (ψ ) から J (ψ )⊥≦ (J (φ ) ∧ΩJ (ψ ))⊥、よって、(6)により J (φ )⊥ ∨ΩJ (ψ )⊥≦ (J (φ ) ∧ΩJ (ψ ))⊥、したがって、(11)と(12)からJ (φ ) ∧ΩJ (ψ ) ≦ (J (φ )⊥∨ΩJ (ψ )⊥)⊥
一方、J (φ )⊥≦ J (φ )⊥∨ΩJ (ψ )⊥、よって 、直モジュラ律によりJ (α ) ∧ΩJ (β ) ≦ (J (φ )⊥∨ΩJ (ψ )⊥) ∧Ω(J (φ )⊥∨Ω (J (φ ) ∧ΩJ (ψ ))) ≦ J (φ )⊥
したがって、{α, β }├ ¬φ は恒真であり、 MT は恒真性を保存する。一方、完全性を証明するには、証明可能でない式は恒真でないこと、云い換えれば、式 φ が証明可能でないならば J (φ ) ≠ 1 となる解釈 J が在ることを示せばいい。それにはいわゆるリンデンバウム代数が利用できる。
以下では「φ ⇔ ψ」をもっぱら「(φ ⇒ ψ ) ∧ (ψ ⇒ φ )」の略記として用いることにして、「φ ⇔ ψ が証明可能である」という関係を考えると、これは NDQL の式全体の集合 Φ 上の同値関係になる。そこで、Ω をこの関係による Φ の分割として、φ の同値クラスを「〔φ〕」と表わすことして、Ω 上の演算 ⊥、∧Ω、∨Ωを次のように定義する。
〔φ〕⊥= 〔¬φ〕, 〔φ〕 ∧Ω〔ψ〕 = 〔φ ∧ ψ〕, 〔φ〕 ∨Ω〔ψ〕 = 〔φ ∨ ψ〕
(これらの定義が有効なためには、φ ⇔ ψ が証明可能ならば、¬φ ⇔ ¬ψ も証明可能で、さらに α ⇔ β が証明可能ならば、(φ ∧ α ) ⇔ (ψ ∧ β ) および (φ ∨ α ) ⇔ (ψ ∨ β ) も証明可能であることが示される必要があるが、その辺は端折ることにする。) Ω 上の順序 ≦ は、通常の束の場合と同様、次のように定義できる。a ≦ b ≡def a ∧Ωb = a
( {φ }├ ψ が証明可能であることと (φ ∧ ψ ) ⇔ φ が証明可能であることは同等だから、〔φ〕 ≦ 〔ψ〕 となることと {φ }├ ψ が証明可能であることは同等だ。) また、文記号 σ をひとつ固定して、1 と 0 を次のように定義する。1 = 〔σ ∨ ¬σ〕, 0 = 〔σ ∧ ¬σ〕
すると、これらによって Ω は直モジュラ束となる。(一般に、このようにして論理の形式系から得られる代数系をリンデンバウム代数と云う。) Ω では直モジュラ律が成り立つことだけを次に示しておく。〔χ〕 ≦ 〔φ〕 かつ 〔ψ〕 ≦ 〔φ〕⊥ とすれば、{χ }├ φ および {ψ }├ ¬φ が証明可能だから、
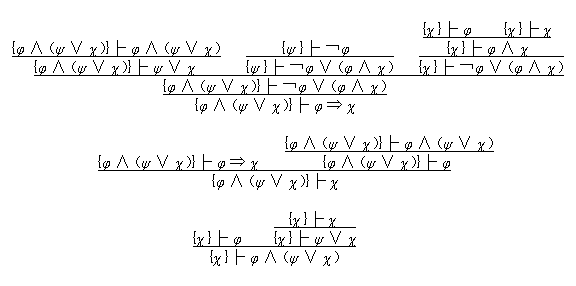
これで完全性が示せる。まず、式全体の集合 Φ から Ω への写像 J を
J (φ ) = 〔φ〕
として定義すれば、J は解釈となる。そこで、ψ を証明可能でない式とすれば、ψ ⇔ (σ ∨ ¬σ ) は証明可能ではない。( σ ∨ ¬σ は証明可能だから、もし (σ ∨ ¬σ ) ⇒ ψ が証明可能だとすれば、モドゥス・ポネンスにより ψ が証明可能となって矛盾をきたす。)したがって、J (ψ ) = 〔ψ〕≠〔σ ∨ ¬σ〕 = 1。なお、量子述語論理については、245から246ページ目にかけて、次のようなくだりがある。
古典論理のように、(量子的)普遍量化子 (universal quantifier) は連言のように振舞い、(量子的)存在量化子 (existential quantifier) は選言のように振舞う。「∧」と「∨」についての四つの導入規則と消去規則のうち、「∨E」だけが非古典的なので、量化子規則のうち、「存在量化子消去」だけが非古典的であろうことが考えられる。事実、量子論理において存在量化子消去は、「∨E」とまったく同じ仕方で制限されているのである。原文は次の通り。
・ ・ ・ 古典的規則は、すでにあらたまってこういうには及ばない。すなわち、いくつかの前提 Γ に基づいて、存在的限量命題「(∃x )Px 」が証明されたと仮定せよ。換言すれば、Γ├ (∃x )Px が証明されたと仮定せよ、である。ゆえに Γ が与えられていれば、われわれが知らなくても、「P 」はある個体について真となるであろう。したがって、「P 」が真である個体を a とし、「a 」で表そう――「a 」は任意の名辞であり、変項のことも定項のこともまったく語っていない。「Pa 」を仮定したとき、もしわれわれが追加諸前提 Γ1の(あるいは空)集合を用いて結論 C を導くことができるならば、われわれは Γ, Γ1├ C を推論することができる。すなわち、Γ と Γ1のどちらも与えられていれば、われわれは C を導くことができるのである。なぜなら、C の導出において、対象 a「P 」のどちらが真であったかは問題ではないからである。さらに、Γ1に課される制限がある。すなわち、「a 」は Γ1に現れるべきではない。
最後の量子論理的制限はいままでと異なっており、より厳しいものである。それは、Γ1が空でなければならないことである。すでに言及したことを思い出せば、∨E を制限することの意味は、分配律を導出できなくすることにある。
存在量化子について制限することの意味は、存在量化子 (∃x )Px ∧ (∃y )Qy├ (∃x )(∃y )(Px ∧ Qy ) にかんして「∧」の分配を止められることにある。
As in classical logic, the (quantum) universal quantifier behaves like conjunction and the (quantum) existential quantifier like disjunction. Of the four introduction and elimination rules for & and ∨, only ∨E is nonclassical, so we can expect that of the quantifier rules only ‘existential quantifier elimination’ will be nonclassical. In fact, in quantum logic it is restricted in exactly the same way ∨E is.これは次のような意味だろう。(ただし、適宜修正を加えた。)
The clasical rule . . . is already tedious enough to state: suppose you have proved an existentially quantified proposition (Ex )Px on the basis of some premises Γ. In other words, you have provedΓ├ (Ex )Px
Then given Γ, P is going to be true of some individual though we do not know of which. So let the individual of which P is true be a, named by a where a is an arbitrary name, strictly speaking neither a variable nor a constant. If, having asuumed Pa, we can, with a set (possibly empty) of additional premises Γ1, derive a conclusion C which is independent of a, then we can infer thatΓ, Γ1├ C.
That is, given both Γ and Γ1, we can derive C because in deriving C it does not matter which object a P was true of. There is a further restriction to be placed on Γ1, namely that a should not occur in Γ1.
The final quantum logical restriction is different, and more severe. It is that Γ1 has to be empty. The effect of restricting ∨E is, as we recall, to make the distributive law underivable. The effect of the restriction on the existential quantifier is to block the distribution of & over the existential quantifier(Ex )Px & (Ey )Qy├ (Ex )(Ey )(Px & Qy ). (p.140f)
古典論理においてと同様、(量子的)普遍量化子は連言[の論理結合子]のように振る舞い、(量子的)存在量化子は選言のように振る舞う。∧ および ∨ に関する導入規則と除去規則で非古典的なのは ∨E だけだから、量化規則のうち「存在量化子除去」だけが非古典的なことが予想できる。実際、量子論理において、件の規則は ∨E の場合と全く同様に制限される。NDQL を述語論理に拡張するには、変数や述語記号等を導入し、式の定義を改めたりする必要があるが、その辺は一切端折って、以下に、量化子に関わる推論規則だけを挙げておく。(なお、話を簡単にするために、定数記号と関数記号は考えに入れないことにして、自由変数を「a 」、束縛変数を「x 」で表わす。)
その古典的規則は ・ ・ ・ あらためて述べるまでもないが、次の通りだ。或る前提 Γ にもとづいて存在量化命題 ∃x Px が証明されているとする。云い換えれば、Γ├ ∃x Px
が証明済みだとする。すると、Γ を仮定すれば、P は何らかの個体について、仮令その個体を我々が知らなくとも、真であることになる。件の個体を a とし、それを a と名付ける。a は任意の名辞であり、厳密に云えば、変数でも定数でもない。そこで、付加的前提の(空であり得る)集合 Γ1とともに Pa を仮定して、a に依存しない結論 C を導くことができれば、Γ, Γ1├ C
と推論できる。つまり、P がどの対象 a について真なのかは C を導くのに関わらない訳だから、Γ および Γ1を仮定すれば C を導くことができる。ただし、 Γ1には、a がそこに現われてはならないという制限が加えられる必要がある。
量子論理における最後の制限は、それとは別で、そして、もっと厳しい。それは、Γ1が空でなければならないというものだ。承知のように、∨E に対する制限は分配律を導くことを不可能にする。存在量化子に対する制限は存在量化子を越えての ∧ の分配∃x Px ∧ ∃y Qy├ ∃x ∃y (Px ∧ Qy )
を阻む。
| ∀導入 |
Γ├ ∀x φ(x ) |
(ただし、a は Γ に属すどの式にも含まれていてはならない。) | |||||||||||||||
| ∀除去 |
Γ├ φ(a ) |
||||||||||||||||
| ∃導入 |
Γ├ ∃x φ(x ) |
||||||||||||||||
| ∃除去 |
Γ├ ψ |
(ただし、a は ∃x φ(x ) にも ψ にも含まれていてはならない。) | |||||||||||||||
| 標準的∃除去 |
Γ ∪ (Δ - {φ(a )})├ ψ |
(ただし、a は ∃x φ(x ) にも ψ にも Δ - {φ(a )} に属すどの式にも含まれていてはならない。) |
2004年秋 大熊康彦
雑録 / 『量子論理の限界』について ( I ) ( II ) ( III ) ( IV ) ( V )