『量子論理の限界』について ( II )
- 形而上学(あるいは超‐物理学) (Meta-physics)
- 自然哲学者のための量子力学 ( I ) (Quantum mechanics for natural philosophers ( I ))
- 波動‐粒子の2重性 (Wave-particle duality)
- コペンハーゲン解釈 ( I ) (The Copenhagen interpretation ( I ))
- コペンハーゲン解釈 ( II ) (The Copenhagen interpretation ( II ))
- 自然哲学者のための量子力学 ( II ) (Quantum mechanics for natural philosophers ( II ))
- 射影公準 (Projection postulates)
- 非局所性と隠れた変数 (Nonlocality and hidden variables)
- 使い勝手の量子論理 (A user-friendly quantum logic)
- 量子論理 (Quantum logic: what it can and can't do)
158ページ目には次のようなくだりがある。
物理空間において位置を表すベクトル空間は実(リアル)である。その空間内で、あるベクトルに実数を掛ければ別のベクトルを生みだすことができる。そのベクトルはもとのベクトルと同じ方向で、掛ける数が1より大きいか小さいかによってもとのベクトルより長いか短いかする。したがって、通常の物理空間は実在的なものの場を満たすベクトル空間であるということができる。というのは、われわれの空間内に存するベクトルに複素数を掛けても意味がない ・ ・ ・ からである。原文は次の通り。
The space of vectors which represent positions in physical space is real in that you can multiply a vector by a real number and produce another vector, in the same direction, lengthend or shortend depending on whether the number is greater or less than 1. Therefore one says that ordinary physical space is a vector space over the field of reals, for mutiplying a vector in our space by complex number makes no sense. . . . (p.89)これは次のような意味だろう。
物理的空間内の位置を表わすヴェクトルからなる空間は、そのヴェクトルに実数を掛けることが出来て、それによって、もとのヴェクトルと同じ向きで、掛けられる数が1より大きいか小さいかに応じて長いか短いかする別のヴェクトルが得られるという点で、実空間だ。そこで、通常の物理的空間は実数体上のヴェクトル空間であると云われる。物理的空間内のヴェクトルに複素数を掛けることは意味をなさないからだ。ここで「通常の物理的空間」と云われているのは、常識的な意味での三次元空間だ。普通この空間はユークリッド空間と看做されるが、三次元ユークリッド空間は、そこに直交座標系をひとつ固定して考えれば、三次元実ヴェクトル空間 R3 と同一視できる。一方、量子力学が扱う状態ヴェクトルの属す空間は、ヴェクトル空間ではあるものの、実ヴェクトル空間ではない。
158から162ページ目にかけては次のようなくだりがある。
状態ベクトルは、その名が示唆するとおり加算可能である。これだけのことは重ね合わせの原理から帰結する。本当に重要なのは、どんな状態ベクトルでも他の状態ベクトルの和で表せることであり、よくあるように、せいぜい数えられる程度の[少数ベクトルの]和になっている。どんな状態ベクトルでも、適切に選ばれた直交する状態ベクトルの和として表すことができる。二つの状態ベクトル f と g は、その内積がゼロである場合、すなわち、原文は次の通り。<f |g > = 0
である場合にのみ直交である。・ ・ ・ 量子力学のヒルベルト空間は、以下の点を除けばわれわれの実‐物理空間と同じベクトル空間である。第1に、ヒルベルト空間は3次元に制限されない点。第2に、ヒルベルト空間のベクトルに複素数を掛けて別の空間のメンバーのベクトルを生むことができる点。第3に、ヒルベルト空間内のベクトルはすべて単位長さ(ゼロベクトル以外)をもっている点。第4に、その元[要素]は物理空間における位置というよりも、量子系の状態に関連するものと解釈される点である。・ ・ ・ ヒルベルト空間の構造は当然、以下のように定義される次元という概念をもつことが許される。ある状態ベクトルがあり、それはいくつかの状態ベクトルの集合の元をどんな割合で足し合わせても(いくつかであれ、そのすべてであれ)生みだすことができないものとせよ(割合は一般に複素数となる)。もとの状態ベクトルはその集合と線形に独立であるということができる。すると、すべてのメンバーが残りの状態ベクトルと線形の独立な状態ベクトルの集合が得られる。ゆえに、相互に線形独立な状態ベクトルのうち、もっとも大きな集合のサイズがヒルベルト空間の次元である。
およそこのことのうちで興味深い二つの点は、量子力学的ヒルベルト空間が複素数場の全体を満たすベクトル空間であることと、その次元が1から加算可能な無限数までのうちのある整数となっていることである。(完全を期すならば、無限次元性といえば通常の3次元空間では眼に見えない位相的な捉えがたさが生じ、概してわれわれには直接関与しないものがもたらされるというべきであろう。)・ ・ ・ いくつかの仕方においては、あるヒルベルト空間は実‐3次元空間とまったく似ていない。1個の電子の状態空間は無限次元である。しかし、この無限のサイズには境域が置かれている。ヒルベルト空間はただ線形に独立な状態ベクトルの加算的な無限性をもつことができるにすぎない、とつねに仮定されている。このことは、厳密な位置に対応する固有状態が存在しないことを意味する。・ ・ ・
一つの量子系、たとえば1個の電子があるとし、位置と運動量についての情報を与える状態ベクトルの集合を考えよう。さしあたりスピンは問題にしないことにする。明らかに、数えられなくはない無限の可能な電子の状態が存在し、それゆえに、数えられなくはない無限の状態ベクトルが存在する。したがって、厳密な位置のついての状態ベクトルは存在しえないということが帰結する、あるいは帰結するといっても差し支えはなかろう。仮にそのような状態ベクトルが存在するならば、厳密な位置についての数えられなくはない無限の状態ベクトルが存在しなければならない。さもなくば、状態ベクトルが線形に独立ではなくなるからであり、状態ベクトルは確かにこうであらねばならない。しかしながら、好きなだけ短くできるがゼロではない間隔を示す位置 x, y, z を除いて、どこででも消えてしまう状態ベクトルが存在することができる。まったく同じことが運動量についてもいえる。
State-vectors can be added, as their name suggests. This much follows from the superposotion principle. Just as important is the fact that any state-vestor can be represented as a sum, as it happens at most a countable sum, of other state-vectors. We can represent any state-vector as a sum of suitably chosen orthogonal state-vectors. Two state-vectors f and g are orthogonal if and only if their inner productこれは次のような意味だろう。(ただし、適宜修正を加えた。)<f |g > = 0.
. . . The Hilbert spaces of quantum mechanics are vector spaces just like our real physical space except first that they are not restricted to being three-dimensional, second that you can multiply their vectors by complex numbers to produce another member of the space, third that the vectors in them are all of unit length (except the zero vector), and fourth that their elements are interpreted as being associated with the states of quantum systems rather than with locations in a physical space.. . . A Hilbert space naturally has enough structure to have a dimension, an idea which is defined as follows. Consider a state-vector which cannot be built out of the elements of some set of state-vectors by adding (some or all of) them together in some proportions. (The proportions will be conplex numbers in generall.) The original state-vector is said to be linearly independent of the set. One can have a set of state-vectors which is such that every member of it is linearly independent of the rest. The size of the largest set of mutually linearly independent state-vectors is then the dimension of the Hilbert space.
The two interesting points in all this are that quantum-mechanical Hilbert spaces are vector spaces over the field of complex numbers and that their dimension may be any integer from 1 to a countable infinity. (For completeness one should say that infinite dimensionality generates topological subtleties not apparent in our ordinary 3-space which by and large are not concern us.). . . In some ways some Hilbert spaces are very unlike real 3-space. The space of states of an electron is infinite dimensional. But a bound is placed on the size of this infinity. It is allways asumed that a Hilbert space can have no more than a countable infinity of linearly independent state-vectors. This implies that there are no eigenstates of exactposition. . . .
Imagine a quantum system, an electron say, and consider the set of state-vectors which give information about position and momentum. Foerget about spin for the time being. Clearly there is nondenumerable infinity of possible electron states and therefore a nondenumerable infinity of state-vectors. It follows, or very nearly follows, that there can be no state-vectors for exact position. If there were there would be a nondenumerable infinity of them since otherwise they would not be linearly independent, and this they surely would have to be. There can however be state-vectors which vanish everywhere except for values of position x, y, and z in nonzero intervals as small as you like. Exactly similar remarks go for momentum. (pp.89-91)
状態ヴェクトルは、その名が示唆するように足し合わすことができる。これは重ね合わせ原理に由る。同じく重要なのは、どんな状態ヴェクトルも、他の複数の、ただし必ずしも有限ではなく可算箇であり得る状態ヴェクトルの和として表わされるということだ。どんな状態ヴェクトルも、適当に撰ばれた直交する状態ヴェクトルの和として表わすことが出来る。ふたつのヴェクトル f と g が直交するのは、それらの内積がゼロの場合、つまり線形独立性についてもう少し精しく云えば、ヴェクトル空間 V の空でない有限部分集合 {v1, . . . , vn } が線形独立なのは、スカラーのどんな n 項列 { λi }i についても、その少なくともひとつの項 λk が 0 でないならば Σi λi vi (= (λ1v1 + . . . + λnvn ))≠ 0 となる場合であり、V の無限部分集合 M が線形独立なのは、M の空でないどんな有限部分集合も線形独立な場合だ。ゼロヴェクトルだけからなるヴェクトル空間 0 を除けば、どんなヴェクトル空間も線形独立な部分集合を含む。したがって、V が 0 でないならば、V の線形独立な部分集合全体の集合には(いわゆるツォルンの補題によって)包含関係の順序において極大な要素が在る。そうした V の極大な線形独立部分集合はひとつではないが、それらは凡て同じ濃度――直観的に云えば、サイズ――をもつので、その濃度によって V の次元が定義される。つまり、V の次元とは、その線形独立な部分集合の濃度のうちで(濃度の順序において)最大なもののことだ。なお、普通、0 の次元は 0 とされるが、以下では、「有限次元」と云うときには、ゼロ次元は考えに入れないものとする。<f |g > = 0
となる場合であり、その場合に限る。・ ・ ・ 量子力学におけるヒルベルト空間は、次の点を除けば実物理空間と同様のヴェクトル空間だ。第一に、ヒルベルト空間は三次元とは限らない。第二に、そのヴェクトルに複素数を掛けることで当の空間の別のメンバーが得られる。第三に、その要素は物理空間内の位置にではなく量子系の状態に関わるものと解釈される。・ ・ ・ ヒルベルト空間は、次元をもつに足る構造を自ずと備えている。この次元というアイディアは、次のように定義される。或るヴェクトルの集合の要素(の幾つかあるいは凡て)をどんな割合で足し合わせても得られないヴェクトルを考える。(割合[つまりスカラー]は一般に複素数になる。)そのような場合、そのヴェクトルは件の集合と線形独立であると云われる。ヴェクトルの集合には、そのどのメンバーも自余のメンバーと線形独立であるようなものが在るが、そうした線形独立な集合のうち、最も大きなもののサイズがそのヒルベルト空間の次元だ。
以上のうちで興味深いのは、量子力学のヒルベルト空間は複素数体上のヴェクトル空間であること、そして、それらの次元は何れかの正整数かあるいは可算無限であることの二点だ。(念入りに云えば、無限次元性は通常の三次元空間では明らかでない位相的な微妙さを孕んでいるが、我々は、だいたいにおいて直接それに関わることはない。)・ ・ ・ 或る点では実三次元空間とは非常に異なるヒルベルト空間も在る。ひとつの電子の状態が属す空間は無限次元だ。ただし、この無限のサイズには制限が在って、ヒルベルト空間は、可算無限箇を超える線形独立な状態ヴェクトルをもつことはないと恒に仮定されている。これは、厳密な位置についての固有状態は存在しないことを含意する。 ・ ・ ・
ひとつの量子系、例えばひとつの電子を想定して、位置と運動量についての情報をもたらす状態ヴェクトルの集合を考える。さしあたりスピンは無視するとしても、明らかに非可算無限箇の可能な電子状態が在り、よって、非可算無限箇の状態ヴェクトルが在る。厳密な位置に関する状態ヴェクトルは在り得ないことが、正確にとはいかないが、ほぼ帰結する。もし在れば、それらは線形独立でなければならないが、だとすると非可算無限であることになるだろうからだ。しかし、任意に小さい空でない区間に属す位置 x 、y 、z についての値を除いて、いたるところでゼロになる状態ヴェクトル[つまり波動関数]は在り得る。全く同様のことが運動量についても云える。
一般に、ヒルベルト空間は、実数体あるいは複素数体上の内積空間(つまり内積を伴なうヴェクトル空間)で、その内積から定まるノルムに関して完備なものとして定義され、係数体の違いに応じて「実」か「複素」を付けて呼び分けられたりするが、ここでは、「ヒルベルト空間」と云えば、もっぱら複素ヒルベルト空間を意味する。(ちなみに、完備とは、要するに実数の場合と同じように極限をとる操作が出来るということだ。)また、量子力学においては、普通、ヒルベルト空間には、可分性――可算で稠密な部分集合を含むこと――が要請される。例えば、標準的な内積を伴なう有限 n 次元複素ヴェクトル空間 Cn は可分なヒルベルト空間だ。可分なヒルベルト空間の次元は正整数かあるいは可算無限であり、無限のサイズの制限というのはこれに由る。(どうして可分性が求められるのか? そもそも何故ヒルベルト空間なのか? 歴史的には、いわゆる有限自由度の量子力学は、1925年から '26年にかけて、ハイゼンベルクのマトリクス力学およびシュレーディンガーの波動力学というふたつの異なった形をとって現われた訳だが、それらを数学的に整合的に統一したのはフォン・ノイマンだった。(von Neumann の Die Mathematische Grundlagen der Quantenmechanik は1932年に刊行されている。)マトリクス力学においてオブザーヴァブルを表わすマトリクスは、平方総和可能な複素数列全体からなる可算無限次元内積空間 l 2 上の作用素と考えられる一方、波動力学における波動関数は、その平方積分が担う役割の重さからして、自然に、対象となる系の配位空間 Ω から複素数全体の集合 C への関数のうちルベーグ可測で平方積分可能なもの全体の集合を「ほとんど到るところ等しい」という同値関係によって分割して得られる可算無限次元内積空間 L2(Ω) のヴェクトルと看做せる。フォン・ノイマンは、l 2 と L2(Ω) が(いわゆるリース‐フィッシャーの定理により)内積空間として同型であることに注目し、それらに共通の構造を抽象すれば量子力学の基本理論が得られるはずだと考え、件の構造を可分で完備な複素内積空間として規定したのだった。そうして生まれたのがヒルベルト空間フォーマリズムだ。可分性はこのフォーマリズムにおいて本質的なようで、例えば、いわゆる正準交換関係の表現の一義性に関するフォン・ノイマンの定理や、「グリーソンの定理」と呼ばれる確率解釈にとって重要な定理は、それなしには成り立たないらしい。)
ところで、有限 n 次元内積空間 V には、正規直交基底と呼ばれる互いに直交する単位ヴェクトル(つまり規格化されたヴェクトル)の n 項列 {vi }i が在って、V のどんなヴェクトル v についても v = Σi <vi , v >vi となる。(ただし「< , >」は内積を表わす。ギビンズが用いている内積等の記法はディラックに由るものだが、そのディラック流の内積は、いわゆる共役空間が関わるスカラー積と切り離せないもので、量子力学においては一般的らしいが、数学では、普通、使われないようだ。以下では両方を適当に使い分けることにする。)第二章で説明されている電子の z 方向についてのスピン状態を表わすヴェクトルの対 { |z, +>, |z, -> } は(標準的な内積を伴なう)複素ヴェクトル空間 C2 の正規直交基底であり、{ |x, +>, |x, -> } と { |y, +>, |y, -> } もまたそうだ。同様に、可算無限次元ヒルベルト空間 H にも、完全正規直交系とか正規直交基底と呼ばれるヴェクトル(の無限)列 {vi }i ∈N が在って、どんな自然数 i と k についても、i = k ならば <vi , vk > = 1、i ≠ k ならば <vi , vk > = 0、そして、H のどんなヴェクトル v についても v = Σi <vi , v >vi となる。(ちなみに、正規直交基底は線形独立だ。)はじめの段落で云われているのはこのことだ。
162から164ページ目にかけては次のようなくだりがある。
量子力学では、オブザーバブルはヒルベルト空間にかんするエルミート演算子に結びつけられる。このことは、オブザーバブルの固有値――その可能な決定値――が複素数ではなく実数であることを保証する。どんなオペレーター A についても、状態ベクトル |f > と |g > が原文は次の通り。<g |A†|f > = <f |A|g >
であると要請することによって、A のエルミート共役量 A†を定義することができる。
オペレーター A は、そのエルミート共役量と等しい場合にのみエルミート的[線形積分可能]である。どのオブザーバブルの固有値も実数であると考えられるので、その順序が線形であり、かつ可能な実験結果と同じであることが保証される。
オブザーバブルはごく自然に、射影作用素 (projection operator) と呼ばれるオペレーターの関係クラスに結びつけられる。射影作用素 P は冪等 [P 2 = P] であり、これはいわば「一度で十分」ということである。
したがって、どんな状態ベクトル |f > についても、P (P |f >) = P |f >
が成り立つ。
・ ・ ・ ヒルベルト空間の部分空間は、加算法のもとに閉じた状態ベクトルの集合である。 |f > と |g > とが部分空間 S のメンバーであれば、 S は、c1|f > + c2|g >
・ ・ ・ 第1に重要な点は、部分空間と射影作用素とが1対1に対応していることである。部分空間は状態ベクトルの集合であり、射影作用素はある状態ベクトルをその部分空間のなかに射影するのである。
In quantum mechanics observables are assosiated with Hermitian operators on Hilbert space, this to ensure that their eigenvalues ―― their possible determinate value ―― are real rather than complex. For any operator A one can define its Hermitian conjugate A† by requiring that for any state-vectors |f > and |g >これは次のような意味だろう。(ただし、適宜修正を加えた。)<g |A†|f > = <f |A|g >.
An operator A is Hermitian if and only if it is equal to its Hermitian conjugate. The eigenvalues of any observable are expected to be real to ensure that their ordering is linear, and is the same as the possible results of experiment.
It is natural to assosiate observables with a related class of operators called projection operators. A projection operator P is idemporent, which is to say ‘once is enough’. For any state-vector |f >P (P |f >) = P |f >.
. . . A subspace of a Hilbert space is a set of state-vectors closed under addition. if |f > and |g > are members of a subspace S then so isc1|f > + c2|g >.
. . . The first important point is that subspaces and projection operators are in one-to-one correspondence. A subspace is the set of state-vectors into which some projection operator projects any state-vector. (p.91f.)
量子力学においては、オブザーヴァブルはヒルベルト空間上のエルミート作用素に結びつけられる。これにより、それらの固有値――在り得る確定値――が複素数ではなく実数であることが保証されることになる。どんな作用素 A についても、その共役作用素 A†を、次のように要請することによって、定義できる。(「<g |A†|f >」は |g > と A†|f > の内積を表わすものと考えていい。「<f |A|g >」も同様で、「 *」は複素共役をとる演算を表わす。)どんな状態ヴェクトル |f > と |g > についても
作用素 A がエルミート的であるのは、A が、その共役作用素 A†に等しい場合であり、その場合に限る。どんなオブザーヴァブルの固有値にも、それらの間の順序が線形であることおよび在り得る実験結果と同種のものであることを確保するために、実数であることが求められる。
<g |A†|f > = <f |A|g >*
オブザーヴァブルが射影作用素と呼ばれる作用素のクラスに結びつけられるのは自然なことだ。射影作用素 P は冪等だ。これは「一回でたくさん」ということで、どんな状態ヴェクトル |f > についてもP (P |f >) = P |f >
・ ・ ・ ヒルベルト空間の部分空間は、加法とスカラー倍に関して閉じたヴェクトルの集合だ。 |f > と |g > が部分空間 S のメンバーであれば、c1|f > + c2|g >
もまた S のメンバーだ。・ ・ ・ まず重要なのは、部分空間と射影作用素は一対一に対応しているということだ。どんな部分空間についても、凡ての状態ヴェクトルをその中に射影する射影作用素が在る。
無限次元の場合を考慮に入れて云えば、ヒルベルト空間 H の空でない部分集合 M が H の部分空間であるのは、それが H の線形部分集合(つまりスカラー倍と和について閉じた部分集合)であり、さらにノルムに関して閉じている(つまり M に含まれるどんな基本列も M の中に極限をもつ)場合だ。H の有限次元線形部分集合は凡て H の部分空間だ。(ちなみに、H の線形部分集合はヴェクトル空間であり、部分空間はヒルベルト空間だ。)
ここでは、「作用素」と云えば、もっぱらヒルベルト空間 H 上の線形作用素、つまり H の線形部分集合 L から H への写像 A で、L に属すどんなヴェクトル v と w およびどんなスカラー λ と μ についても A(λv + μw ) = λAv + μAw となるものを意味する。H が無限次元の場合には、凡ての作用素が共役作用素をもつ訳ではなく、共役作用素は、定義域が稠密な作用素に対してだけ定義される。共役作用素は随伴作用素とも呼ばれ、エルミート作用素は自己随伴作用素とも呼ばれる。自己随伴作用素の固有値は凡て実数だ。また、射影作用素は、自己随伴で冪等な有界作用素として定義される。(H 上の作用素 A は、その定義域が H 全体で、或る実数 c が在って H のどんなヴェクトル v についても ||Av || ≦ c ||v || (つまり
第二章に述べられていることを、この枠組の中であらためてまとめてみれば、次のようになるだろう。
量子力学的系 S の状態は適当なヒルベルト空間 H に属す単位ヴェクトル v によって表わされる。(ただし、状態ヴェクトル v において本質的なのは、それが H のどの一次元部分空間に属すかであり、v と同じ一次元部分空間に属す単位ヴェクトル――云い換えれば、v に絶対値が 1 の複素数を掛けたヴェクトル――は何れも v と同じ状態を表わすものとされる。)また、S に関するオブザーヴァブル O は H 上の自己随伴作用素 opO によって表わされる。opO が固有値 λ をもつ場合、λ は O がとり得る値のひとつであり、v によって表わされる状態についての O の期待値 <O > は、v が opO の定義域に属していれば、<v, opOv > に等しい。
なお、第二章では「系の状態ヴェクトルとオブザーヴァブルに対応する作用素に関する知識から、その系について件のオブザーヴァブルを測定した結果の値が任意に撰んだ範囲に含まれる確率を計算できる」と云われている訳だが、その計算法――いわゆる統計的アルゴリズム――については、ギビンズはほとんど触れることがない。それを簡単にまとめておけば以下の通り。
一般に、ヒルベルト空間 H 上のどんな自己随伴作用素 A についても、そのスペクトル族と呼ばれる射影作用素の族 { PA(λ ) }λ∈R がひとつだけ在って、H のどんなヴェクトル v および A の定義域に属すどんな w についても次が成り立つ。
<v, Aw > =∫λd <v, PA(λ )w >
ただし、右辺はいわゆるリーマン‐スティルチェス積分であり、積分範囲は実数全体の集合 R の全体にわたるものとする。(これを A のスペクトル分解と云う。)そこで、R 上の区間 Δ = ( λ, μ ] (= { x ∈ R | λ < x ≦ μ } )に対して、PA(Δ ) をPA(Δ ) = PA(μ ) - PA(λ )
として定義すれば、これも射影作用素であり、A が系 S に関するオブザーヴァブル O を表わす場合、単位ヴェクトル v によって表わされる状態にある S について O を測定した結果の値が Δ に収まる確率は||PA(Δ )v ||2(= <PA(Δ )v, PA(Δ )v > = <v, PA(Δ )v >)
に等しいものとされる。(射影作用素の一般的属性から、v が単位ヴェクトルならば、0 ≦ ||PA(Δ )v ||2 ≦ 1 となり、||PA(Δ )v ||2 = 1 となるのは v が PA(Δ ) の値域 ranPA(Δ ) に属す場合かつその場合だけだ。また、区間 Γ と Δ が共通部分をもたなければ ranPA(Γ ) と ranPA(Δ ) は直交する。(つまり Γ ∩ Δ = Ø ならば ranPA(Γ ) に属すどんなヴェクトルも ranPA(Δ ) に属す凡てのヴェクトルと直交する。)よって、区間 Θ が共通部分をもたない区間 Γ と Δ の和集合であれば ||PA(Θ )v ||2 = ||PA(Γ )v ||2 + ||PA(Δ )v ||2 となる。)さらに、A が固有値 λ をもてば、O の測定結果が λ とでる確率は、P を λ に対応する固有空間――つまり λ に対応する固有ヴェクトルの全体およびゼロヴェクトルからなる部分空間――を値域とする射影作用素として、||Pv ||2 に等しいものとされる。(A が λ のほかに固有値 μ をもてば、λ に対応する固有空間と μ に対応する固有空間は直交する。)ところで、H が有限 n 次元ならば、H 上の自己随伴作用素 A は 1 以上 n 以下の m 箇の固有値をもつ。それらを(後の便宜のために)小さい順に λ1, . . . , λm として、(i ≦m となるそれぞれの正整数 i に対して) Li を λi に対応する固有空間とすれば、L1, . . . , Lm は互いに直交し、H をスパンする。(つまり、i ≠ k ならば Li と Lk は直交し、L1, . . . , Lm の凡てを集合論的に包含する部分空間は H そのもの以外にない。)そこで、Pi を Li を値域とする射影作用素とすれば、次が成り立つ。
A = Σi λi Pi
(これも A のスペクトル分解と呼ばれる。)これらの射影作用素と A のスペクトル族 { PA(λ ) }λ∈R の関係は次の通り。P0 をゼロ作用素(つまり凡てのヴェクトルをゼロヴェクトルに対応づける作用素)として、R から H 上の射影作用素全体の集合への写像 P (つまり射影作用素の族 { P (λ ) }λ∈R )を次のように定義する。
- μ < λ1 ならば P (μ ) = P0
- λk ≦ μ < λk +1 ならば P (μ ) = Σ i ≦k Pi (ただし 1 ≦ k ≦ m - 1)
- λm ≦ μ ならば P (μ ) = Σ i ≦m Pi
∫λd <v, P (λ )w > = Σi λi <v, Pi w > = <v, Aw >
となるから、(A のスペクトル族の唯一性により) { P (λ ) }λ∈R = { PA(λ ) }λ∈R となる。この場合、どんな実数 λ と μ についても λ < μ ならば ranPA(λ ) ⊆ ranPA(μ ) (つまり PA(λ ) の値域は PA(μ ) の値域の部分空間)となることが写像 P の定義から見てとれるが、これは、実は、スペクトル族を特徴づける属性のひとつであり、次元の如何に関わらず恒に成り立つ。
一般に、ヒルベルト空間 H 上の自己随伴作用素 A に対して、{ PA(λ ) }λ∈R をそのスペクトル族として、
{ λ ∈ R | どんな正の実数 δ についても PA(λ - δ ) ≠ PA(λ + δ ) }
を A のスペクトルと云う。A の固有値全体の集合は A のスペクトルの部分集合であり、点スペクトルと呼ばれ、スペクトルから点スペクトルを除いた残りの集合は連続スペクトルと呼ばれる。H が有限次元ならば、凡ての自己随伴作用素は点スペクトルだけをもつが、無限次元の場合には、連続スペクトルしかもたないものも在る。A がオブザーヴァブル O を表わしていれば、O がとり得る値全体の集合は A のスペクトルに等しいものと考えられる。165から166ページ目には次のようなくだりがある。
量子論理はまず第1に束 (lattice) の特殊論理である。束とは半順序関係と1対の演算とをもった一つの集合であり、その演算――交わり (meet) と結び (join) ――は集合内で閉じている。集合が命題の集合であっても、交わりと結びという属性は、基本的な属性と考えられる連言と選言にそれぞれ対応する。原文は次の通り。
半順序関係は、反射的か反対称的かつ推移的関係である。それゆえに、集合論的な包含 (inclusion) は集合が集積したものにかんする半順序関係である。
量子系に結びつけられるヒルベルト空間の部分空間は、その系についての命題に対応し、そしてまさに、ヒルベルト空間の全領域についての特殊な部分集合である。
量子論理的束においては、元はそのようなヒルベルト空間の部分空間である。つまり半順序関係は、部分空間の集合にかんして定義された集合論的な包含である。交わりという演算は集合論的な共通部分 (intersection) であるが、結びという演算は集合論的な合併集合 (union) ではなく、重ね合わせの原理によって決まるゆえにスパンである。・ ・ ・ こうした束を論理として書き換えるならば、つまり束を代数構造としてではなく、論理構造として表現するならば、包含関係は、交わりが「かつ」に、結びが「または」に対応する。
Quantum logic is first of all a special sort of lattice.これは次のような意味だろう。
A lattice is a set with a partial ordering relation and a pair of operations ―― a meet and join ―― which are closed on the set. If the set is a set of propositions the properties of the meet and join correspond to the expected basic properties of conjunction and disjunction respectively.
A partial ordering relation is reflexive, antisymmetric and transitive. Therefore set-theoretic inclusion is a partial ordering relation on a colloction of sets. The subspaces of a Hilbert space associated with a quantum system correspond to propositions about that system and are special subsets of the overall domain of the Hilbert space. In the lattice which is quantum logic the elements are the subspaces of such a Hilbert space, the partial ordering relation is set-theoretic inclusion defined on the set of subspaces. The operation of meet is set-theoretic intersection but the operation of join is not set-theroretic union but span for reasons which depend on the superposition principle. . . . When one transcribes this lattice as a logic, (when you represent it as a logic rather than as an algebraic structure) the inclusion relation corresponds to ‘implication’, the meet to ‘and’ and the join to ‘or’.(p.92f.)
量子論理は何よりまず特種の束だ。半順序集合 L は、そのどんな要素 a と b についても下限 inf{a, b } と上限 sup{a, b } が在るとき、束と呼ばれる。その場合、L 上の二項演算(つまり L × L から L への写像)∧L および ∨L を
束は半順序関係および一対の閉じた演算――交わりと結び――をもつ集合だ。交わりと結びのもつ属性は、連言および選言の論理結合子に当然のこととして求められる基本的属性に一致する。
半順序関係は、反射的かつ反対称的かつ推移的だ。よって、集合論的包含は集合の集まりの上の半順序関係だ。量子系に結びつけられるヒルベルト空間の部分空間は、その系についての命題に対応するが、部分空間は、件のヒルベルト空間のヴェクトル全体の特殊な部分集合だ。量子論理である束においては、その要素はそうしたヒルベルト空間の部分空間であり、半順序関係は部分空間の集合上で定義された集合論的包含だ。交わりの演算は集合論的積である一方、結びの演算は集合論的和ではなく、重ね合わせ原理に依る理由から、スパンだ。・ ・ ・ この束を論理として書き換えれば(つまりそれを代数的構造としてではなく論理として表わせば)、包含関係は「含意」に、交わりは「かつ」に、結びは「または」に対応する。
a ∧Lb = inf{a, b }, a ∨Lb = sup{a, b }
として定義すれば、次が成り立つ。
| 冪等律 | a ∧La = a, a ∨La = a | |||||||||
| 交換律 | a ∧Lb = b ∧La, a ∨Lb = b ∨La | |||||||||
| 結合律 | a ∧L(b ∧Lc ) = (a ∧Lb ) ∧Lc, a ∨L(b ∨Lc ) = (a ∨Lb ) ∨Lc | |||||||||
| 吸収律 | a ∧L(a ∨Lb ) = a, a ∨L(a ∧Lb ) = a |
a ≦ b ≡def a ∧Lb = a
(ただし、「≡def 」は、その左辺が右辺によって定義されることを意味する。)ヒルベルト空間のふたつの部分空間の集合論的積(つまり共通部分)はまた部分空間だが、集合論的和(つまり合併)は一般に部分空間ではない。ふたつの部分空間のスパンとは、それらを集合論的に共に包含する部分空間すべての共通部分――云い換えれば、それらを共に包含する部分空間のうちで包含関係の順序において最小のもの――のことだ。
つづいて、量子力学の基本言語 ELQM (the elementary language of quantum mechanics) なるものが登場する。ELQM の基本文 (basic sentence) は次のような形をしている。
時刻 t において、系 S に関する力学的変数 d の値は範囲 Δ の中に在る。(原著p.93)
一般に力学的変数の値は実数とは限らないが、運動量のようなヴェクトル量も成分ごとに見れば実数な訳で、話を実数値の場合に限っても問題はない。そこで、力学的変数(つまりオブザーヴァブル)d は実数全体の集合 R に値をとるものとすれば、系 S に結びつけられるヒルベルト空間 H の上には、先に述べたように、d を表わす自己随伴作用素 opd および R 上の区間 Δ に対応して射影作用素 Popd (Δ ) が在って、区間 Γ が Δ の部分集合ならば Popd (Γ ) の値域 ranPopd (Γ ) は ranPopd (Δ ) の部分空間であり、Γ と Δ が共通部分をもたなければ ranPopd (Γ ) と ranPopd (Δ ) は直交し、||Popd (Δ )v ||2 = 1 となるのは v が ranPopd (Δ ) に属す場合かつその場合だけとなり、単位ヴェクトル v によって表わされる状態にある S について d を測定した結果の値が Δ に収まる確率は ||Popd (Δ )v ||2 に等しいものとされる。こうしたことがらを拠りどころとして、「時刻 t において、系 S に関する力学的変数 d の値は範囲 Δ の中に在る」という基本文は部分空間 ranPopd (Δ ) に結びつけられ、この文が真となるのは時刻 t における S の状態ヴェクトルが ranPopd (Δ ) に属す場合かつその場合だけだとされる。また、「時刻 t において、系 S に関する力学的変数 d の値は範囲 Δ の中に在る」という文と「時刻 t において、系 S に関する力学的変数 f の値は範囲 Γ の中に在る」という文の連言が真となるのは、S の時刻 t における状態ヴェクトル v が ranPopd (Δ ) と ranPopf (Γ ) の共通部分に属す場合かつその場合だけだとされ、それらの選言が真となるのは、v が ranPopd (Δ ) と ranPopf (Γ ) のスパンに属す場合かつその場合だけだとされる。(ちなみに、古典力学においては、n 箇の質点からなる系 S の状態は、ひとつの直交座標系における各質点の x 、y 、z 座標を表わす計 3n 箇の実数とそれらに対応する運動量成分を表わす計 3n 箇の実数の組によって表わすことが出来る。そうした実数の 6n 項列は 6n 次元実ヴェクトル空間 R6n のヴェクトルと看做せるから、S の力学的変数 d は R6n から R への写像と考えられる。(ちなみに、この場合の R6n は解析力学で「相空間」と呼ばれるものの一例だ。また、x 、y 、z 座標だけを考えれば、それらが属す R3n は「配位空間」と呼ばれるものの一例になる。)すると、R 上の区間 Δ がひとつ指定されれば、d (v ) ∈ Δ となるようなヴェクトル v 全体の集合が定まる訳で、ELQM と同様の基本文を考えれば、それは、R6n の部分空間にではなく、そうした部分集合に対応し、連言は集合論的積に、選言は集合論的和に対応する。(射影作用素に相当するのは部分集合のいわゆる特性関数だ。)
次に、電子のスピンに関する簡単な例が示される。170から171ページ目には次のようなくだりがある。
ヒルベルト空間におけるどの状態ベクトルも、一つの重ね合わせとして表してよいことをわれわれは知っている。つまり、選ばれたどんな方向についても、スピン「上向き」状態と「下向き」状態との重みの和として表してもよいのである。その重みは複素数 ci で、原文は次の通り。Σi ci = 1
そこで、便宜のために z 方向を選択する。1個の電子があり、そのスピンは z 方向にではなく、x 方向に「上向き」であるものと仮定しよう。
「α」を、その電子が x 方向にスピン「上向き」である ・ ・ ・ ことを主張する(本当にそうなっているのだが) ELQM 文であるとし、「β」と「χ」を、z 方向にそれぞれスピン「上向き」および「下向き」である ・ ・ ・ ことを主張する ELQM 文であるとしよう。
選言「β ∨ χ」は部分空間全体に合致し、したがって真である。「α ∧ (β ∨ χ)」に対応する部分空間は「α」に合致する部分空間である。
束論の術語でいえば、a ∧ (b ∨ c ) = a
しかし、「α ∧ β」と「α ∧ χ」のどちらにも合致する部分空間はゼロベクトルのみを含む集合であり、したがって「α ∧ β」と「α ∧ χ」の選言に合致する部分空間もそうである。それゆえに、a ∧ (b ∨ c ) ≠ (a ∧ b ) ∨ (a ∧ c )
となる。
量子論理においてはきわめて一般的に、この式の右辺は「論理的により強い」とされ、必ずしも換位的ではないがつねに左辺を含意している。この換位があてはまらないときには、分配性もあてはまらない。
We know that any state-vector in the Hilbert space [the two-dimensional Hilbert space of a spin-1/2 system] may be represented as a superposition, a weighted sum (the weights are complex numbers ci which are such that Σi |ci |2 = 1) of ‘up’ and ‘down’ spin states for any chosen direction. So choose the z -direction for convenience. Suppose that we have an electron whose spin is ‘up’ not in the z -direction but in the x -direction.これは次のような意味だろう。(ただし、適宜修正を加えた。)
Let a be the sentence of ELQM that asserts (truly as it happens) that the electron has spin ‘up’ in the x -direction. And let b and c be the sentences of ELQM which assert that S has spin ‘up’ and ‘down’ respectively in the z -direction. The disjunction b ∨ c corresponds to the whole subspace and so is true, and the subspace corresponding to a & (b ∨ c ) is the subspace corresponding to a. In the lattice-theroretic termsa ∧ (b ∨ c ) = a.
But the subspace corresponding to both a & b and a & c is empty and so is the subspace corresponding to their disjunction. Thereforea ∧ (b ∨ c ) ≠ (a ∧b ) ∨ (a ∧ c ).
Quite generally in quantum logic the right-hand side of this expression is ‘logically stronger’ and always implies the left-hand side though not always conversely. When this converse fails so does distributivity. (p.94f.)
[電子のようなスピン 1/2 の系に結び付けられる二次元の]ヒルベルト空間のどんな状態ヴェクトルも、任意に撰ばれた方向について「上向き」と「下向き」のスピン状態の重ね合わせつまり重み付き和として表わせることを我々は知っている。(重み c1 と c2 は、|c1|2 + |c2|2 = 1 となるような複素数だ。)そこで、便宜上 z 方向を採って、 z 方向にではなく x 方向について「上向き」のスピンをもつ電子を考える。この場合、L|x, +> を |x, +> が属す C2 の一次元部分空間とし、また、L|z, +> を |z, +> が属す一次元部分空間、L|z, -> を |z, -> が属す一次元部分空間とすれば、基本文(の省略的変形ヴァージョン)a 、b 、c にそれぞれ対応する部分空間は L|x, +> 、L|z, +> 、L|z, -> だ。L|z, +> と L|z, -> のスパンは C2 であり L|x, +> と C2 の共通部分は L|x, +> であるのに対して、L|x, +> と L|z, +> の共通部分も L|x, +> と L|z, -> の共通部分も共にゼロヴェクトルだけからなる部分空間であり、よって、それらのスパンもまたゼロヴェクトルだけからなる部分空間だ。
a を、その電子が x 方向について「上向き」のスピンをもつことを(この場合ただしく)述べるELQM 文とし、b と c を、それぞれその電子が z 方向について「上向き」および「下向き」のスピンをもつことを述べる ELQM 文とする。選言 b ∨ c は空間全体に対応し、よって真であり、a ∧ (b ∨ c ) に対応する部分空間は a に対応する部分空間だ。つまり、束論的に表わせばa ∧ (b ∨ c ) = a
しかし、a ∧ b および a ∧ c にはゼロヴェクトルだけからなる部分空間が対応し、よって、それらの選言に対応するのも同じ部分空間だからa ∧ (b ∨ c ) ≠ (a ∧ b ) ∨ (a ∧ c )
量子論理においては、全く一般的に、この表現の右辺は、左辺より「論理的に強い」のであり、恒に左辺を含意するが、逆[つまり左辺が右辺を含意すること]は必ずしも成り立たない。逆が成り立たない場合には、分配性が成り立たない訳だ。
ところで、古典論理では、「A ∧ (B ∨ C ) ⇔ (A ∧ B ) ∨ (A ∧ C )」という形の文は恒真だ。また、「A ∨ (B ∧ C ) ⇔ (A ∨ B ) ∧ (A ∨ C )」という形の文も恒真であり、これらのことは、「分配律」と呼ばれる論理法則を具現するものとなっている。一方、上の結果は、量子論理においては、「A ∧ (B ∨ C ) ⇔ (A ∧ B ) ∨ (A ∧ C )」という形の文は恒真でないことを示している。この分配律の破れは、量子論理に関わる唯一最重要な事実だとギビンズは云う。
175から177ページ目にかけては次のようなくだりがある。
量子論理であるところの束には、交わりと結びという二進法的な演算だけでなく、第3の基本的な演算、すなわち直交補空間化 (orthocomplementation) というもう一成分の演算がある。交わりと結びは「かつ」と「または」に対応する。直交補空間化は「でない」に対応する。量子論理は直交相補束 (orthocomplemented lattice) であり、ちょっとした追加構造をもっているが、量子論理を古典的にするほどの、すなわちブール代数にするほどの追加構造ではない。原文は次の通り。
形式的には、量子論理は次のような、基本集合を L とする束 Q である。Q = <L, 1, 0, ⊆, ∧, ∨, ⊥>
この式は以下を満たす。
(1) a ∧ b ⊆ a
(2) a ∧ b ⊆ b
(3) c ⊆ a かつ c ⊆ b ならば、c ⊆ a ∧ b
およびその双対は以下のようになる。
(4) a ⊆ a ∨ b
(5) b ⊆ a ∨ b
(6) a ⊆ c かつ b ⊆ c ならば、a ∨ b ⊆ c
(1)から(3)までと(4)から(6)までは、それぞれ結びと交わりの基本的属性である。(1)から(6)までが与えられているとき、双対原理が成立している。すなわち、束にかんするどの定理についても、∧ と ∨ 、⊆ と ⊇ を交換することによってもうひとつ別の束が得られる。
「否定」についてはどうか? いかなる直交相補束においても最大元 1 と最小元 0 があり、これらは L におけるすべての a について、
(7) a ⊆ 1 かつ
(8) 0 ⊆ a
となっている。
直交補空間化は L における各元をその直交補空間へと写像する。すなわち、⊥ : L → L 、したがって ⊥ : aa⊥と書ける。したがって、以下のようになる。
(9) a ∨ a⊥= 1
(10) a ∧ a⊥= 0
(11) a ⊆ b ならば、b⊥⊆ a⊥
(12) (a⊥)⊥= a
直交補空間化である「否定」は「無矛盾の原理」、「排中律」および「2重否定の法則」を満足する。
(1)から(12)までは、直交束 (ortho-lattice) として知られる特殊な束――これは直交補空間化を重ねた普通の束にすぎないのだが――が備えている構造をつかまえている。量子論理はこうした多くの構造をもっており、あるものはそれ以上の構造をもっている。「直交モジュラ律」として知られるさらに別の公理から量子論理が得ている追加構造をつかまえることができるのである。・ ・ ・
有限次元ヒルベルト空間の部分空間の束はモジュラである。これは以下を満たす。c ⊆ a であれば、
モジュラ性とは分配性が弱められることを表している。
a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
無限次元ヒルベルト空間の場合、これは量子力学において一般に関心がもたれる場合であるが、モジュラ性さえあてはまらず、分配性はさらに弱められねばならない。無限次元ヒルベルト空間の閉部分空間の束は直交モジュラである。すなわちこれは以下を満たす。c ⊆ a かつ b ⊆ a⊥であれば、
分配性が無限次元の場合でさらに弱められるのは、二つの無限次元の部分空間のスパンが「有限ベクトル」を含んでいるからである。このベクトルは二つの部分空間についてのベクトルの有限和からつくられることはなく、そのようなベクトルの無限級数の和からのみつくられる。
a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
As well as the binary operations of meet and join the lattice which is quantum logic has a third primitive operation, the unary operation of orthocomplementation. Meet and join correspond to ‘and’ and ‘or’. Orthocomplementation corresponds to ‘not’. Quantum logic is an orthocomplemented lattice with a bit of extra structure but not enough extra structure to make it classical, that is a Boolean algebra.これは次のような意味だろう。(ただし、適宜修正を加えた。)
Formally, quantum logic is the lattice Q whose base set is L such thatQ = <L, 1, 0, ≦, ∧, ∨ ⊥>
which satisfies(1) a ∧ b ≦ a
and their duals
(2) a ∧ b ≦ b
(3) if c ≦ a and c ≦ b then c ≦ a ∧ b(4) a ≦ a ∨ b
The conditions (1) to (3) and (4) to (6) are the basic properties of the join and meet respectively. Given (1) to (6) the principle of duality holds: for any theorem concerning a lattice you can get another by interchanging ∧ and ∨ and ≦ and ≧ (where a ≦ b if and only if b ≧ a ).
(5) b ≦ a ∨ b
(6) if a ≦ c and b ⊆ c then a ∨ b ≦ c.
What about ‘negation’?
In any orthocomplemented lattice there are a maximum element 1 and a minimum element 0 which, for all a in L, are such that(7) a ≦ 1,
The orthocomplementation maps each element in L to its orthocomplement
(8) 0 ≦ a.⊥ : L → L
such that
⊥ : aa⊥
(9) a ∨ a⊥= 1
A ‘negation’ which is an orthocomplementation satisfies the ‘principle of noncontradiction’, ‘the law of excluded middle’ and ‘double negation’.
(10) a ∧ a⊥= 0
(11) if a ≦ b then b⊥≦ a⊥
(12) (a⊥)⊥= a.
Conditions (1) to (12) capture the structure possesed by a particular kind of lattice known as an ortholattice ―― which is no more than an unspecial lattice with an added orthocomplementation. Quntum logic has this much structure and some more. One can capture the extra structure that quantum logic has by a further axiom known as the ‘orthomodular law’. . . .
The lattice of subspace of a finite- dimensional Hilbert space is modular. It satisfiesa ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
Modularity represents a weakning of distributivity.
whenever c ≦ a.
In the infinite-dimensional case, which is the one that is generally of interest in quantum mechanics, even modularity fails and distributivity has to be further weakened. The lattice of closed subspaces of an infinite-dimensional Hilbert space is orthomodular. That is, it satisfiesa ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
Distributivity is further weakened in the infinite-dimensional case because the span of two infinite-dimensional subspaces contains ‘limit vectors’ which cannot be formed from finite sums of vectors from the two subspaces but only from the sum of an infinite series of such vectors. (pp.95-97)
whenever both c ≦ a and b ≦ a⊥.
量子論理である束は、交わりと結びという二項演算だけでなく、第三の基本的演算である直補という単項演算をもっている。交わりと結びは「かつ」と「または」に対応し、直補は「でない」に対応する。量子論理は、少しばかり余計な構造をもった直相補束だ。しかし、この付け足しの構造は、それを古典的なものつまりブール代数にするほどのものではない。ごたごたしていて判りにくいが、要するに、(7)と(8)を充たす特別な要素 1 と 0 をもち、(9)から(12)を充たす単項演算 ⊥ を伴なった束が直相補束であり、量子論理とは直モジュラな直相補束のことだという訳だ。(ここでは、≦ と ∧ と ∨ を伴なった集合 L が束であることが前提になっている。(1)から(6)はどんな束においても成り立つ。)普通、直モジュラな直相補束は単に直モジュラ束と呼ばれるようだ。ちなみに、無条件に「a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )」およびその双対「a ∨ (b ∧ c ) = (a ∨ b ) ∧ (a ∨ c )」を充たす束は分配束と呼ばれる。(なお、「<L, 1, 0, ≦, ∧, ∨, ⊥>」は、集合 L およびその特定の要素 1 と 0、そして L が伴なう関係 ≦ や演算 ∧ 等をまとめて表わしている訳だが、そうして表わされるような、集合と関係や写像等々をひと括りにしたものを「数学的構造」と云う。)
形式的には、量子論理はQ = <L, 1, 0, ≦, ∧, ∨, ⊥>
のような、L を基礎集合とし、以下を充たす束 Q だ。(1) a ∧ b ≦ a
(1)から(3)およびそれらの双対(4)から(6)は、それぞれ結びと交わりのもつ基本的属性だ。(1)から(6)により双対原理が成り立つ。つまり、束に関するどんな定理についても、∧ と ∨ および ≦ と ≧ を交換することで、もうひとつの定理が得られる。(ただし、b ≧ a となるのは a ≦ b となる場合であり、その場合に限る。)
(2) a ∧ b ≦ b
(3) c ≦ a かつ c ≦ b ならば、c ≦ a ∧ b
(4) a ≦ a ∨ b
(5) b ≦ a ∨ b
(6) a ≦ c かつ b ≦ c ならば、a ∨ b ≦ c
「否定」はどうなるか?
どんな直相補束にも、最大要素 1 と最小要素 0 が在り、その基礎集合に属す凡ての a について、次が成り立つ。(7) a ≦ 1
直補 ⊥ は、L の各要素をその直補要素に写す写像
(8) 0 ≦ a⊥ : L → L
であり、次が成り立つ。
⊥ : aa⊥
(9) a ∨ a⊥= 1
直補である「否定」は、「排中律」と「無矛盾原理」[つまり矛盾律]そして「二重否定」を充たす。
(10) a ∧ a⊥= 0
(11) a ≦ b ならば、b⊥≦ a⊥
(12) (a⊥)⊥= a
(1)から(12)の条件は、直相補束として知られる特種の束――これは直補を付加された普通の束でしかない訳だが――がもつ構造を捉えている。量子論理はこれだけの構造に加えて、さらなる構造をもっている。その付け足しの構造は、「直モジュラ律」として知られる公理によって捉えることが出来る。・ ・ ・
有限次元ヒルベルト空間の部分空間のなす束はモジュラだ。つまり、それは次を充たす。c ≦ a ならば
モジュラ性は分配性の弱化を意味する。
a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
量子力学において一般に重要な無限次元の場合には、モジュラ性も破れ、分配性はさらに弱められることになる。無限次元ヒルベルト空間の部分空間のなす束は直モジュラだ。つまり、それは次を充たす。c ≦ a かつ b ≦ a⊥ならば
無限次元の場合に分配性がさらに弱められるのは、ふたつの無限次元部分空間のスパンが、それらふたつの部分空間[の和集合]に属すヴェクトルの有限和ではなく無限級数の和としてのみ得られる「極限ヴェクトル」をもつためだ。
a ∧ (b ∨ c ) = (a ∧ b ) ∨ (a ∧ c )
集合 M の冪集合(つまり M の部分集合全体の集合) P(M ) は、P(M ) を L 、M を 1、空集合を 0、⊆ を ≦、∩ を ∧、∪ を ∨、M における補集合をとる演算を ⊥ と考えれば、分配的かつ直相補的な束つまりブール束になる。(より精しく云えば、P(M ) は完備ブール束をなす。完備とは、この場合、基礎集合のどんな部分集合についても順序関係 ≦ に関して上限と下限が在ることを意味する。)一方、ヒルベルト空間 H の部分空間全体の集合 S(H) は、S(H) を L 、H を 1、ゼロヴェクトルだけからなる部分空間を 0、⊆ を ≦、∩ を ∧、ふたつの部分空間のスパンをとる演算
つづいて、「混合状態」なるものを表わすための道具、密度作用素が導入される。
量子力学が記述するのは個別の系ではなくアンサンブル(つまり統計集団)だとする解釈はアンサンブル解釈と呼ばれるが、ギビンズは、アンサンブル解釈の語り口を一時的に採ると断わった上で、電子のビームの例を用いて混合状態を説明している。
x 方向について上向きのスピンをもつ電子からなるビームと z 方向について上向きのスピンをもつ電子からなるビームを考えると、それらの状態は、第二章で説明されているように、それぞれ C2 の単位ヴェクトル |x, +> および |z, +> によって表わせる訳だが、第一のビームについて z スピンを測定した結果が上向きと出る確率および下向きと出る確率は共に 1/2 で、一方、第二のビームは z 方向について上向きのスピンをもつ電子だけからなる訳だから、それらのビームを例えば等しい割合で混合したビームについて z スピンを測定した結果が上向きと出る確率は 3/4 であり、下向きと出る確率は 1/4 だ。また、同様の混合ビームについて y スピンを測定した結果が上向きと出る確率および下向きと出る確率は共に 1/2 だ。そうした混合ビームのようなアンサンブルの状態が混合状態であり、その統計的属性を表わすのが密度作用素だという訳だ。
179から181ページ目にかけては次のようなくだりがある。
対象、|+x ><+x | について考察してみよう。原文は次の通り。
複素数である <+x ||+x > と違って、すなわち |+x > とその複素共役量 <+x | とのスカラー積と違って、|+x ><+x | は一つのオペレーターである。それを |+y > のような状態ベクトルに掛ければ、|+x >(<+x |+y >)
が得られる。これは括弧内の複素数を掛けた状態ベクトル、|+x > である。
どちらかといえば些細なことであるが、状態ベクトル |+x > は、オペレーター ――後述する理由から密度オペレーターと呼ばれる――によってつぎのように表すことができる。ρ = |+x ><+x |
ρ は |+x > に作用して |+x > を生む。なぜなら、(|+x ><+x |)|+x > = |+x >(<+x |+x >) = |+x >
だからである。ρ はなんらかの他の状態ベクトル |> に作用してふたたび |+x > を生むが、今度はある因子によって縮約されて、つぎのようなスカラー積となることが容易にわかる。<+x |>
しかし、|+x ><+x | は取るに足らない例であり、まったく特殊なケースである。一般的には対象、ρ = Σi λi |i ><i |
(ただしΣi λi = 1、|i > は規格化された状態ベクトル)が密度オペレーターであり、混合状態の記述に用いることができる。・ ・ ・ それぞれ重み λi をもつ |i > によって記述される純粋要素アンサンブルからなら混合状態についての正しい統計値を与えるのである。λ は要素アンサンブルの「密度」を与える。・ ・ ・
しばらくは、密度オペレーターを考察するにあたって、|i > が直交する場合を、すなわちもっと厳密にいえば、i = j ならば <i |j > = 1、およびさもなければ <i |j > = 0 である場合を考察しよう。この場合、 λi がオペレーターの固有値であり、それに対応する固有状態が |i > であることが容易にわかる。
密度オペレーターはオペレーターであるからして、それらを掛け合わせることができる。ある密度オペレーター ρ をそれ自身に掛けて ρ2 を得れば、つぎのようになることが容易にわかる。
そして、もし Σi λi = 1 であれば、1 を除くすべての λi がゼロでないかぎり、Σi λi2 < 1 である。後者の場合、つまり Σi λi2 = 1 のときが、混合状態が真に純粋な場合である。
ρ2 = Σj (Σi λi |i ><i |)|j ><j | = Σi λi2
したがって、これが密度オペレーター ρ の二つの一般属性である。
(1) 0 < ρ2 ≦ 1
(2) もし ρ2 = 1 であれば、ρ は純粋アンサンブルを記述する。
こうした数学的事実は、「純粋な場合」すなわち「純粋アンサンブル」の定義として用いることができ、これは単一の状態ベクトルによって記述されるアンサンブルは均質であるというわれわれの直観と一致する。ρ2 < ρ であれば、ρ は固有混合状態を記述する。ゆえに、純粋アンサンブルは非固有混合状態である。
いかにして密度オペレーターは混合状態についての正しい統計値を与えるのか? 密度オペレーターから統計値を得るための弱いアルゴリズムというものがある。
まずオペレーターのトレースという概念が必要である。
オペレーターのトレースとはその対角線要素の和である。どんな表記(たとえば |i > )にも、オペレーター O のマトリクスをみいだすことができ、そのトレースの値、トレース(O ) = Σi <i |O |i >
は一定となる。これは |i > になにを選んでも同じことがいえる。これはトレースの顕著ではあるが、非常に単純な属性である。
密度オペレーター ρ によって記述される(純粋であれ混合であれ)アンサンブルのあるオブザーバブル O についての期待値が、<O > = トレース (ρO )
のように定式化できると知るのはさほど難しくない。
Consider this objectこれは次のような意味だろう。(ただし、適宜修正を加えた。)|+x ><+x |.
Unlike <+x |+x > which is a complex number, namely the scalar product of |+x > with its complex conjugate <+x |, |+x ><+x | is an operator. If you multiply it into a state-vector like |+y > you get|+x >(<+x |+y >)
which is |+x >, a state-vector, multiplied by the complex number inside the brackets.
One can, rather trivially, represent the state-vector |+x > by the operator ―― called the density operator for reasons we note later ――ρ = |+ x ><+x |.
The operator ρ operates on |+x > to produce |+x > as(|+ ><+ x |)|+ x > = |+ x >(<+ x |+ x >) = |+ x >.
It is easy to see that ρ operates on any state-vector |> to produce |+x > again but this time shrunk by a factor, the scalar product<+ x |>.
But |+x ><+x | is a trivial example and very much a special case.
In general the objectρ = Σi λi |i ><i |
where Σi λi = 1, and the |i > are normalized state-vectors, is a density operator and it can be used to describe a genuine mixture. . . . it gives the correct statics for a mixture composed of pure subensembles each of which is described by the |i > each with weighting λi . The λi give the ‘densities’ of the subensemles. . . .
For now we consider density operators in which the |i > are orthonormal or, more accurately, in which <i |j > = 1 if i = j and = 0 otherwise. In this case it is easy to see that the λi are the eigenvalues of the operator and the corresponding eigenstates are |i >.
Density operators are operators and so you can multiply them. If you multiply a density operator ρ by it self to get ρ2, then it is easy to see thatρ2 = Σi λi 2|i ><i | < 1
If Σi λi = 1, then Σi λi2 < 1, unless all the λs exept for one are zero. In this later case the mixture is really a pure case.
So, here is a general property of density operators ρ.0 < ρ2 ≦ ρ
and if ρ2 = 1 then ρ describes a pure ensemble.
This mathematical fact can be used as a definition of ‘pure case’ or ‘pure ensemble’ which conforms to our intuition that an ensemble described by a single state-vector is homogeneous. When ρ2 < ρ, then ρ describes a proper mixture. A pure ensemble is then a improper mixture.
How do density operators give the right statics for mixtures? There is a neat algorithm for getting the statics from a density operator.
First, we need the idea of the trace of an operator.
The trace of an operator is the sum of its diagonal elements. We can find the matrix of an operator O in any representation (say) |k >, and the value of the tracetrace(O ) = Σi <i |O |i >
will be fixed. It is the same for any choice of |i >. This is a remarkable but very simple property of the trace.
It is not too difficult to see that we can formulate the expectation value for an observable O for an ensemble (pure or mixed) descraibed by the density operator ρ as<O > = trace(ρO ). (pp.98-100)
次の対象を考える。(はじめに出て来る |x, +> とその共役ヴェクトルのスカラー積というのは |x, +> とそれ自体の内積のことだと考えていい。)|x, +><x, +|
<x, +|x, +> つまり |x, +> とその共役ヴェクトル <x, +| のスカラー積は複素数だが、それと違い、|x, +><x, +| は作用素だ。これを |x, +> のような状態ヴェクトルに掛ければ|x, +>(<x, +|x, +>)
つまり括弧内の複素数を掛けられた状態ヴェクトル |x, +> が得られる。
ややトリヴィアルながら、状態ヴェクトル |x, +> は、後に述べる理由から密度作用素と呼ばれる作用素ρ = |x, +><x, +|
によって表わすことが出来る。[ |x, +> は単位ヴェクトルだから <x, +|x, +> = 1、したがって](|x, +><x, +|)|x, +> = |x, +>(<x, +|x, +>) = |x, +>
となるから、この作用素 ρ は |x, +> に作用して |x, +> をもたらす訳だ。ρ が任意の状態ヴェクトル |> に作用して、 今度は或る因子、つまりスカラー積<x, +|>
によって縮んだ |x, +> をもたらすことは容易に判る。
しかし、|x, +><x, +| はトリヴィアルな例であり、全く特殊なケースだ。
一般には、対象ρ = Σi λi |i ><i |
が密度作用素だ。ただし、Σi λi = 1、λi ≧ 0、|i > は規格化された状態ヴェクトル。密度作用素は真正の混合状態を記述するために用いることが出来る。・ ・ ・ それは、重み λi をもつ |i > によって記述される純粋な部分アンサンブルからなる混合状態についての正しい統計をもたらす。λi は部分アンサンブルの「密度」を示す。・ ・ ・
さしあたり、|i > が正規直交、つまり i = j ならば <i |j > = 1、そうでなければ <i |j > = 0 となる場合の密度作用素を考える。この場合、λi がその作用素の固有値であり、対応する固有状態が |i > であることは容易に判る。
密度作用素は作用素だから掛け合わすことが出来る。密度作用素 ρ をそれ自体に掛ければ ρ2 が得られるが、ρ2 = Σi λi 2|i ><i |
となることは容易に判る。Σi λi = 1 だから、ひとつを除く凡ての λ がゼロでない限り Σi λi2 < 1 となる。ひとつを除いて凡ての λ がゼロの場合、対応する混合状態は純粋ケースにほかならない。
密度作用素 ρ の一般的な属性は次の通り。
0 ≦ ρ2 ≦ ρ
[ただし 0 はゼロ作用素。] ρ2 = ρ ならば ρ は純粋アンサンブルを記述する。
この数学的事実は、「純粋ケース」つまり「純粋アンサンブル」の定義として用いることが出来る。それは、単一の状態ヴェクトルによって記述されるアンサンブルは同質であるという我々の直観に適うものだ。ρ2 < ρ となる場合、ρ は固有混合状態を記述する。よって、純粋アンサンブルは非固有混合状態だ。
密度作用素は如何にして混合状態についての正しい統計をもたらすか? そうした統計を密度作用素から得るためのニートなアルゴリズムが在る。
まず作用素のトレースというアイディアが必要だ。
作用素のトレースはその対角線要素の和だ。どんな正規直交基底 |i > に関しても、作用素 O のマトリクスを見出すことが出来て、そのトレースの値trace(O ) = Σi <i |O |i >
が定まる。この値は、どんな正規直交基底をとっても同じだ。これはトレースの、非常に単純ではあるが注目すべき属性だ。
密度作用素 ρ によって記述される(純粋あるいは混合)アンサンブルに関するオブザーヴァブル O についての期待値が<O > = trace(ρO )
として定式化できるのを確かめることはそう難しくない。
ヒルベルト空間 H が有限次元ならば、H 上のどんな有界作用素 A および正規直交基底 {vi }i と {wi }i についても Σi <vi , Avi > = Σi <wi , Awi > となるので、H 上の有界作用素全体の集合から複素数全体の集合への写像 trace を、正規直交基底 {ui }i をひとつ固定して、trace(A ) = Σi <ui , Aui > として定義できる。しかし、H が無限次元だとそうはいかず、trace の定義域は「トレースクラス」と呼ばれる H 上の有界作用素全体の集合の或る部分集合となる。トレースクラスを定義するには、正な有界作用素の平方根の概念が要る。H 上の作用素 A が正であるとは、その定義域に属すどんなヴェクトル v についても <v, Av > ≧ 0 となることを云うが、どんな正有界作用素 A についても、その平方根と呼ばれる正有界作用素 A1/2 がひとつだけ在って、(A1/2)2 = A1/2A1/2 = A となる。(ちなみに、正有界作用素は自己随伴だ。)
ここからは H が可算無限次元の場合に話を限るとして、A が H 上の正有界作用素ならば、H のどんな正規直交基底 {vi }i と {wi }i についても Σi <vi , Avi > = Σi <wi , Awi > となる。(これらの級数は収束するとは限らないが、∞ となる場合も含めて、この等式は成り立つ。)ところで、B が H 上の有界作用素ならば、B †B は正有界作用素なので、その平方根 (B †B )1/2 が在る。そこで、正規直交基底 {ui }i をひとつ固定して、H 上の有界作用素 B で Σi <ui , (B †B )1/2ui > が有限なもの全体の集合を考えれば、それがトレースクラスだ。つまり
トレースクラス = { B は H 上の有界作用素 | Σi <ui , (B †B )1/2ui > < ∞ }
作用素 A がトレースクラスに属せば、H のどんな正規直交基底 {vi }i と {wi }i についても Σi <vi , Avi > と Σi <wi , Awi > は共に(絶対)収束し Σi <vi , Avi > = Σi <wi , Awi > となるので、トレースクラスから複素数全体の集合 C への写像 trace が次のように定義できる。trace(A ) = Σi <ui , Aui >
トレースクラスは作用素の和と複素数倍に関してヴェクトル空間をなし、trace はトレースクラス上の線形汎関数(つまりトレースクラスから C への線形写像)となる。また、次が成り立つ。A が H 上のトレースクラスに属す作用素で B が H 上の有界作用素ならば、AB と BA は共にトレースクラスに属し、trace(AB ) = trace(BA )。ヒルベルト空間 H 上の密度作用素――またの名を「統計作用素」――は、普通、H 上のトレースクラスに属す正作用素でトレースが1であるものとして定義される。上で例にあげられている |x, +><x, +| は C2 の単位ヴェクトル |x, +> が属す一次元部分空間を値域とする射影作用素だが、一般に、H の一次元部分空間を値域とする射影作用素は凡て密度作用素だ。また、上で云われているように、{ λi }i を Σi λi = 1 となる非負実数の(空でない)有限 n 項列、{ Pi }i を H の一次元部分空間を値域とする射影作用素の n 項列とすれば、Σi λi Pi は密度作用素であり、 { λi }i と { Pi }i が無限列の場合も同様だ。(逆に、どんな密度作用素も、そうした有限和か可算和の形に――しかも i ≠ k ならば Pi と Pk それぞれの値域は直交となるように――分解できる。)
なお、作用素の間の関係 ≦ についてギビンズは何も説明を加えていないが、普通、ヒルベルト空間 H 上の自己随伴な有界作用素全体の集合の上には、順序関係 ≦ が次のように定義される。
A ≦ B ≡def H のどんなヴェクトル v についても <v, Av > ≦ <v, Bv >
(この順序関係は、H 上の射影作用素全体の集合の上においては、それぞれの射影作用素の値域の間の包含関係に一致する。)また、ここでも統計的アルゴリズムについて補っておけば、PopO(Δ ) を、オブザーヴァブル O を表わすヒルベルト空間 H 上の自己随伴作用素 opO のスペクトル分解から定まる R 上の区間 Δ に対応する射影作用素とすれば、密度作用素 ρ によって表わされる状態にあるアンサンブルについて O を測定した結果の値が Δ に収まる確率は trace(ρPopO(Δ )) に等しいものとされる。
先の電子ビームの例に戻れば、x 方向について上向きのスピンをもつ電子ビームと z 方向について上向きのスピンをもつ電子ビームの状態は、それぞれ |x, +><x, +| および |z, +><z, +| によって表わされ、それらを等しい割合で混合したビームの状態は (1/2)|x, +><x, +| + (1/2)|z, +><z, +| によって表わされることになるが、この混合ビームについて z スピンを測定した結果が上向きと出る確率は次のようになる。
| trace(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|z, +><z, +|)) | |
| = | <z, +|(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|z, +><z, +|))|z, +> |
| + <z, -|(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|z, +><z, +|))|z, -> | |
| = | (1/2)<x, +|z, +><z, +|x, +> + (1/2)<z, +|z, +> + 0 |
| = | 1/4 + 1/2 |
| trace(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|y, +><y, +|)) | |
| = | <y, +|(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|y, +><y, +|))|y, +> |
| + <y, -|(((1/2)|x, +><x, +| + (1/2)|z, +><z, +|)(|y, +><y, +|))|y, -> | |
| = | (1/2)<x, +|y, +><y, +|x, +> + (1/2)<z, +|y, +><y, +|z, +> + 0 |
| = | 1/4 + 1/4 |
ヒルベルト空間 H の部分空間全体のなす束 L(H) から実数全体の集合 R 上の閉区間 [ 0, 1 ] (= { x ∈ R | 0 ≦ x ≦ 1 } )への写像 p は、次を充たすとき、L(H) 上の確率測度と呼ばれる。
- p (0) = 0、p (H) = 1、ただし 0 はゼロヴェクトルだけからなる部分空間。
-
{ Li }i ∈N が L(H) の要素からなる列で、どんな自然数 i と k についても i ≠ k ならば Li と Lk は直交となる場合、
p (
ただし i Li ) = Σi p (Li )
i Li ) = Σi p (Li )
 i Li は { Li }i ∈ N の凡ての項によってスパンされる部分空間。
i Li は { Li }i ∈ N の凡ての項によってスパンされる部分空間。
H を次元が 2 より大きい可分なヒルベルト空間とすれば、L(H) 上のどんな確率測度 p についても H 上の密度作用素 D がひとつだけ在って、H のどんな部分空間 L についても、PL を L を値域とする射影作用素として、なお、L(H) 上の確率測度は、以下のような意味で、通常の確率測度の拡張になっていると云える。p (L) = trace(DPL)
Ω を空でない集合として、Ω の冪集合の部分集合 F (つまり M ∈ F ならば M ⊆ Ω となるような集合 F )は、次を充たすとき、Ω 上のシグマ集合体と呼ばれる。
- F は空集合を要素としてもつ(つまり Ø ∈ F )。
- M が F に属せば Ω に関する M の補集合も F に属す(つまり M ∈ F ならば Ω - M ∈ F )。
- { Mi }i ∈N が F の要素からなる列ならば、各 Mi のうちの少なくともどれかひとつの要素であるもの全体の集合は F に属す(つまり { Mi }i ∈N ⊆ F ならば ∪i Mi ∈ F )。
- p (Ø) = 0、p (Ω) = 1。
-
{ Mi }i ∈N が F の要素からなる列で、どんな自然数 i と k についても i ≠ k ならば Mi と Mk は共通部分をもたない(つまり Mi ∩ Mk = Ø となる)場合、
p (∪i Mi ) = Σi p (Mi )
B を R 上のボレル集合体とすれば、H 上のどんなスペクトル族 { P (λ ) }λ∈R についてもスペクトル測度と呼ばれる B によって添数づけられた射影作用素の族――云い換えれば B から H 上の射影作用素全体の集合への写像―― { Pm(Δ ) }Δ∈B がひとつだけ在って次が成り立つ。
- どんな実数 λ についても P (λ ) = Pm(( -∞, λ ]) (ただし ( -∞, λ ] = { x ∈ R | x ≦ λ } )。
- R 上のどんな区間 ( λ, μ ] についても P (μ ) - P (λ ) = Pm(( λ, μ ])。
そこで、{ P (Δ ) }Δ∈B をスペクトル測度、v と w を H のヴェクトルとして、mv,w をボレル集合 Δ を <v, P (Δ )w > に対応づける写像とすれば、mv,w は B 上のいわゆる有界変動な複素数値加法的集合関数となる。一方、前に述べたように、H 上のそれぞれの自己随伴作用素には、そのスペクトル分解をなすスペクトル族がひとつづつ対応している訳だが、実は、この対応は一対一なうえに過不足のないものなので、{ P (Δ ) }Δ∈B に対応するスペクトル族にも、それに対応する自己随伴作用素がひとつだけ在ることになる。それを A とすれば、H のどんなヴェクトル v および A の定義域に属すどんな w についても
<v, Aw > =∫R λdmv,w
となり、これも A のスペクトル分解と呼ばれる。(この右辺の積分は mv,w によるいわゆるルベーグ‐スティルチェス積分だが、普通、これも、スペクトル族の場合と同様に、「∫R λd <v, P (λ )w >」と表わされる。)なお、v を単位ヴェクトルとすれば、ボレル集合 Δ を ||P (Δ )v ||2 に対応づける写像は B 上の確率測度であり、先に触れた統計的アルゴリズムは、普通、スペクトル測度を用いて定式化される。つまり、A が量子力学的系 S に関するオブザーヴァブル O を表わす場合には、v によって表わされる状態にある S について O を測定した結果の値がボレル集合 Δ に収まる確率は ||P (Δ )v ||2 に等しいものとされる。(前にスペクトル族に関して述べたことは、そこでの「PA(Δ )」等を自己随伴作用素 A に対応するスペクトル測度のボレル集合 Δ についての値を表わすもの等々と解釈すれば、スペクトル測度についてもそのまま成り立つ。その場合、A が固有値 λ をもてば、λ に対応する固有空間を値域とする射影作用素は PA({ λ }) に等しい。また、H が有限次元のときは、A の、その固有空間を値域とする射影作用素によるスペクトル分解を A = Σi λi Pi とすれば、PA(Δ ) は、λk ∈ Δ となるような固有値 λk に対応する Pk の総和 Σλk∈ΔPk に等しい。)密度作用素を利用するアルゴリズムについても同様であり、したがって、ELQM の基本文に含まれる「範囲 Δ」はボレル集合を意味するものとしていい。ところで、h をボレル集合 Δ を P (Δ ) の値域 ranP (Δ ) に対応づける写像とすれば次が成り立つ。- h (Ø) = 0、h (R) = H。
- どんなボレル集合 Δ についても h (R - Δ ) = (ranP (Δ ))⊥。
- どんなボレル集合 Δ と Γ についても h (Δ ∩ Γ ) = ranP (Δ ) ∩ ranP (Γ )。
-
どんなボレル集合 Δ と Γ についても h (Δ ∪ Γ ) = ranP (Δ )
 ranP (Γ )。
ranP (Γ )。
要するに、H 上のそれぞれの自己随伴作用素には、そのスペクトル測度を介して、L(H) のシグマ完備なブール部分束が対応しており、そうした部分束ひとつひとつの上に限れば、L(H) 上の確率測度は通常の確率測度と看做せる訳だ。
さらに、ヒルベルト空間のテンソル積なるものが導入される。183から184ページ目にかけては次のようなくだりがある。
いかにして二つのヒルベルト空間を結合すべきか? その問題は二つの方法で生ずる。第1に、1個の電子のような単一の量子系について、その位置の関数である状態ベクトルのヒルベルト空間を、固有スピンについての状態ベクトルのヒルベルト空間と結合することができる。第2に、そしてより重要なこととしては、異なるが相互作用する二つの量子系を記述したいであろうから、そのヒルベルト空間を、それぞれもとのヒルベルト空間と結合してもよい。この第2の場合は、測定プロセスの量子力学的説明を与えようとしたとき、つまり測定系を被測定系と相互作用する第2の量子力学的系として扱おうとしたときに生ずるケースである。原文は次の通り。
HI と HII をそれぞれ系 I と II に結びつけられるヒルベルト空間であるとし、fI と fII をそれぞれ HI と HII に属する状態ベクトルであるとしよう。
二つのヒルベルト空間のテンソル積 HIHII は、「積」ベクトル fIfII によってスパンされる。fI と fII とが具体的な表記で(たとえば波動関数として)与えられるならば、その積は単純にそれらを掛け合わすことによって得られる。
およそこのことの要点はなにか? 第1に、テンソル積空間の次元は、二つのヒルベルト空間の次元の積であることに注目しよう。第2に、もし系 I と II とが相関していれば、したがって、もし系 I が状態 fIi にあれば、したがって系 II は状態 fIIi にあることになっていれば、次のことが帰結する。この結合系の状態は、fIifIIi
のような項の重ね合わせとなり、これらの項はすべてゼロ係数をもった「反対」項で表される。言い換えれば、相関系の状態は、Σi fIifIIi
で与えられねばならず、これは fIifIIj という形の項を一つももっていない。ただし i ≠ j。
One last question: How should we combine two Hilbert spaces?これは次のような意味だろう。(ただし、適宜修正を加えた。)
The problem arises in two ways. First, for a single quantum system like an electron one can combine the Hilbert space of its state-vevtors which are functions of position with the Hilbert space of state-vectors for its intrinsic spin. Second and less trivially, one may want to describe, and hence combine the Hilbert space of, two different but interacting quantum systems each with its own Hilbert space. This second case is one that arises when one tries to give a quantum-mechanical account of the measuring process, treating the measuring system as a second quantum-mechanical system interacting with the measured system.
Let H1 and H2 be two Hilbert spaces, associated with the system I and II, and let f1 and f2 be state-vectors belonging to the H1 and H2 respectively. The tensor product H1H2 of the two Hilbert spaces is spanned by the ‘product’ vectors f1f2. If f1 and f2 are given concrete representations (say as wave-functions) then their product is obtained by simply multiplying them.
What is the point of all this? First note that the dimension of the tensor product space is the product of the dimensions of the two Hilbert spaces. But if the systems I and II are correlated, so that if I is in the state f1,I and II is in the state f2,II then the state of the combined system is a superposition of terms likef1,IIf2,II
with all the ‘cross’ terms having zero coefficients. (p.101)
残る問いは、ふたつのヒルベルト空間をどうやって結合するか、ということだ。ここで「積」と云われているのは、いわゆるヴェクトル積ではなく、ヴェクトルの順序対のことで、ヒルベルト空間 H1 と H2 の直積集合 H1× H2 から以下を充たすようなテンソル積ヒルベルト空間 H1
この問題は二通りの仕方で生じる。第一に、ひとつの電子のような単独の量子系に関して、位置の関数であるその状態ヴェクトル[つまり波動関数]の属すヒルベルト空間を、その固有スピンについての状態ヴェクトルの属すヒルベルト空間と結合したい場合。これはトリヴィアルだが、第二のケースはそうでもなくて、それは、相互作用している異なるふたつの量子系を記述するために、それぞれに伴うヒルベルト空間を結合したい場合だ。この第二のケースは、測定プロセスについて、測定系を被測定系と相互作用する第二の量子力学的系として扱って、量子力学的説明を与えようとする際に生じる。
H1 と H2 をそれぞれ系 I および II に結びつけられたふたつのヒルベルト空間とし、f1 と f2 をそれぞれ H1 および H2 に属す状態ヴェクトルとする。
ふたつのヒルベルト空間のテンソル積 H1H2 は、「積」ヴェクトル f1f2 によってスパンされる。f1 と f2 が(たとえば波動関数として)具体的な表現を与えられれば、この積は単純にそれらを掛け合わすことによって得られる。
以上の要点は何か? まず、テンソル積空間の次元は、ふたつのヒルベルト空間の次元の積であることに注意せよ。また、系 I と II とが、もし系 I が状態 f1,i にあれば系 II は状態 f2,i にあるというように相関している場合には、その結合系の状態はf1,i f2,i
のような項の重ね合わせであり、凡ての「交差」項の係数はゼロだ。
-
{vi }i と {wk }k がそれぞれ H1 および H2 の正規直交基底ならば { (vi , wk ) }i,k は H1
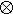 H2 の正規直交基底。
H2 の正規直交基底。
-
複素数のどんな(空でない)有限 m 項列 { λi }i と n 項列 { μk }k および H1 のヴェクトルのどんな m 項列 {vi }i および H2 のヴェクトルのどんな n 項列 {wk }k についても
(Σi λi vi , Σk μk wk ) = Σi Σk λi μk (vi , wk )
-
H1 のヴェクトルのどんな(空でない)有限 m 項列 {vi }i と n 項列 {wk }k および H2 のヴェクトルのどんな m 項列 {si }i と n 項列 {uk }k についても
<Σi (vi , si ), Σk (wk , uk )> = Σi Σk<vi , wk >1<si , uk >2
(ただし、「< , >」は H1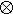 H2 の内積を表わし、「< , >1」と「< , >2」はそれぞれ H1 および H2 の内積を表わす。)
H2 の内積を表わし、「< , >1」と「< , >2」はそれぞれ H1 および H2 の内積を表わす。)
-
A と B がそれぞれ H1 および H2 上の有界作用素ならば、それらに対応して H1
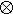 H2 上の有界作用素 C がひとつだけ在って、次が成り立つ。
H2 上の有界作用素 C がひとつだけ在って、次が成り立つ。
複素数のどんな(空でない)有限 mn 項列 { λi,k }i,k および H1 のヴェクトルのどんな m 項列 {vi }i と H2 のヴェクトルのどんな n 項列 {wk }k についても
C (Σi Σk λi,k (vi , wk )) = Σi Σk λi,k (Avi , Bwk )
この C を「A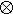 B 」と表わす。
B 」と表わす。
-
A と B を H1 上の有界作用素、C と D を H2 上の有界作用素とすれば、次が成り立つ。
(A
 C )(B
C )(B  D ) = (AB )
D ) = (AB )  (CD )
(CD )
(A + B ) C = A
C = A  C + B
C + B  C, A
C, A  (C + D ) = A
(C + D ) = A  C + A
C + A 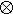 D
D
- A と B がそれぞれ H1 および H2 上の自己随伴作用素ならば、それらに対応して H1
-
D が H1
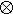 H2 上の密度作用素ならば、それに対応して H1 上の密度作用素 D1 および H2 上の密度作用素 D2 がそれぞれ唯ひとつづつ在って、次が成り立つ。
H2 上の密度作用素ならば、それに対応して H1 上の密度作用素 D1 および H2 上の密度作用素 D2 がそれぞれ唯ひとつづつ在って、次が成り立つ。
H1 上のどんな自己随伴有界作用素 A についても
trace1(D1A ) = trace(D (A
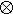 I2 ))
I2 ))
H2 上のどんな自己随伴有界作用素 B についても
trace2(D2B ) = trace(D (I1
(ただし、「I1」と「I2」はそれぞれ H1 および H2 上の恒等作用素(つまり各ヴェクトルをそれ自体に対応づける作用素)を表わし、「trace1」と「trace2」はそれぞれ H1 および H2 に関するトレース、「trace」は H1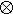 B ))
B ))
 H2 に関するトレースを表わす。)D1 と D2 を D のリダクションと云う。
H2 に関するトレースを表わす。)D1 と D2 を D のリダクションと云う。
複素数のどんな(空でない)有限 mn 項列 { λi,k }i,k および A の定義域に属すヴェクトルのどんな m 項列 {vi }i と B の定義域に属すヴェクトルのどんな n 項列 {wk }k についても
C (Σi Σk λi,k (vi , wk )) = Σi Σk λi,k (Avi , Bwk )
この C を「A2003年夏(2004年3月増補改訂) 大熊康彦
雑録 / 『量子論理の限界』について ( I ) ( II ) ( III ) ( IV ) ( V )