雑録

---

『量子論理の限界』について ( III )

1. 形而上学（あるいは超‐物理学）　(Meta-physics)
2. 自然哲学者のための量子力学 ( I )　(Quantum mechanics for natural philosophers ( I ))
3. 波動‐粒子の２重性　(Wave-particle duality)
4. コペンハーゲン解釈 ( I )　(The Copenhagen interpretation ( I ))
5. コペンハーゲン解釈 ( II )　(The Copenhagen interpretation ( II ))
6. 自然哲学者のための量子力学 ( II )　(Quantum mechanics for natural philosophers ( II ))
7. 射影公準　(Projection postulates)
8. 非局所性と隠れた変数　(Nonlocality and hidden variables)
9. 使い勝手の量子論理　(A user-friendly quantum logic)
10. 量子論理　(Quantum logic: what it can and can't do)

*

　第七章は測定に関することがらにあてられている。
　１８６から１８７ページ目にかけては次のようなくだりがある。

　まず第１に、そして伝統的物理理論にとっては例外的に、「測定」という言葉が量子力学の基本公理――たとえば第２章の第３原理――のなかに現れており、この点で量子物理学は、全体として古典力学とはまったく異なっている。・ ・ ・
　たとえば、光を使って１個の古典粒子の反跳を観測するものとしよう。古典的な説明では、被観測系に起こる擾乱は任意に小さくすることができ、「原理的には」その系を任意の精度で観測することができる。・ ・ ・ 実際には、測定には熱力学に基づくような、あらゆる種類の制約がある。しかしこれらは、われわれが考察している理論によって、すなわち古典力学によって課される制約ではない。・ ・ ・
　量子力学における測定は、古典物理学における測定とはまったく異なっている。それがどのように異なるのかを厳密に述べようとすると、量子力学の哲学においては容易に論点先取を犯しかねない。しかし正統的見解においては、量子系についてのシュレーディンガー方程式は一般に測定プロセスの間に破れる。

　原文は次の通り。

　 First of all, and unusually, the word ‘measurement’ figures in the fundamental axioms of quantum mechanics ―― in principle (3) of chapter 2 for example ―― and in this quantum physics is quite unlike classical physics as a whole. . . .
　 For example, suppose you observe a classical particle using light bounced off it. In the classical account you can make the disturbance on the observed system as small as you like and, ‘in principle’, you can observe the system with arbitrary accuracy. . . . Of course, in practice there are all sorts of limitations on measurement. There are also some theoretical limitations, like those due to thermodynamics. But these are not the limitations imposed by the theory we are considering, namely classical mechanics. . . .
　 Measurement in quantum mechanics is quite different from measurement in classical physics. One can easily beg questions in the philosophy of quantum mechanics if one says exactly how it is different. But in the orthodox view, the Schrödinger equation for a quantum system generally breakes down during the measuring process. (p.102)

　これは次のような意味だろう。

　まず、尋常でないことに、量子力学の基本公理――例えば第二章の原理（３）――においては「測定」という語が重要な位置を占めており、この点で、量子物理学は古典物理学全体と全く異なっている。・ ・ ・
　例えば、ひとつの古典論的粒子を、そこから跳ね返る光によって観測するものとする。古典論的説明では、観測の対象である系に対する攪乱は望むだけ小さくできて、「原理的には」、任意の精度で件の系を観測できる。・ ・ ・ もちろん、実際には、測定にはあらゆる類の制約がある。また、熱力学に依るような理論的な制約もある。しかし、それらは、我々が考えている当の理論、つまり古典力学によって強いられる制約ではない。・ ・ ・
　量子力学における測定は、古典物理学における測定とはかなり異なる。その違いを、量子力学の哲学において問題とされることがらを前提とすることなく、精しく述べるのは難しい。しかし、正統的見解によれば、一般に量子系に関するシュレーディンガー方程式は測定過程の間に破れる。

　ここでシュレーディンガー方程式について簡単に触れておく。
　古典力学の場合と同様、量子力学においても、（いわゆるシュレーディンガー描写によれば）系 S の状態は一般に時間に連れて変化する。これは（ヒルベルト空間フォーマリズムにおいては）S の状態を表わすヒルベルト空間 H のヴェクトルが時間に連れて替わっていくことを意味し、形式的に云えば、S の状態の時間発展は時間軸（としての実数体）R から H への写像 Ψ によって表わされる。すると、H はノルムに関して完備だから、普通の関数の場合と同様に Ψ の微分が考えられる訳で、どんな実数 t についてもヴェクトル v が在って、

||((Ψ (t + x ) - Ψ (t ))/x ) - v || → 0　( x → 0 )

（つまり、どんな正（の実）数 ε についても正数 δ が在って、ゼロでないどんな実数 x についても |x - t | ＜ δ ならば ||((Ψ (t + x ) - Ψ (t ))/x ) - v || ＜ ε ）となるとき、Ψ は微分可能であると云われる。Ψ が微分可能ならば、それぞれの t に対応して v がひとつだけ在って上を充たすので、この対応によって R から H への写像がひとつ定まる。その写像を「(d /dt )Ψ 」と表わす。（なお、Ψ は、どんな実数 t についても

||Ψ (t + x ) - Ψ (t ) || → 0　( x → 0 )

となるとき、連続であると云われる。連続でなければ Ψ は微分可能ではない。）
　系 S の状態の時間発展は、H を S のハミルトニアン――つまり S の全エネルギーを表わす H 上の自己随伴作用素――として、次のような微分方程式の解によって表わされる。

(d /dt )Ψ = HΨ

（ただし、i = -1、 = h/2π、h はプランク定数。）時間に依るシュレーディンガー方程式と呼ばれるこの方程式の解は、v を H の定義域に属す単位ヴェクトルとして、Ψ (0) = v という条件――いわゆる初期条件――のもとで唯ひとつであり、以下のように定まる。
　{ P (Δ ) }_{Δ ∈B} を H 上の射影作用素からなるスペクトル測度、f を R から複素数全体の集合 C への連続関数――より一般には、いわゆるボレル可測関数――とすれば、それらに対応して H 上の作用素 A がひとつだけ在って、次が成り立つ。

• A の定義域は∫_Rf ^*(λ )f (λ )d <v, P (λ )v > が有限となる v 全体の集合、つまり

  domA = { v ∈ H |∫_Rf ^*(λ )f (λ )d <v, P (λ )v > ＜ ∞ }

• H のどんなヴェクトル v および domA に属すどんなヴェクトル w についても

  <v, Aw > =∫_Rf (λ )d <v, P (λ )w >

特に、指数関数 exp をとって、実数 t に対して f (λ ) = exp(itλ ) として、この t をパラメタとしてもつ関数 f について上を充たす作用素 A を「U_t 」と表わすことにすれば、U_t は H 上の有界作用素であり、U_t^†U_t = U_tU_t^† = I となる。（ただし I は H 上の恒等作用素。）したがって、U_t はユニタリ作用素であり、さらに、族 { U_t }_{t ∈R} はいわゆる連続１パラメタユニタリ群となる。そこで、{ P (Δ ) }_{Δ ∈B} を系 S のハミルトニアン H に -1/ を掛けて得られる自己随伴作用素 (-1/)H のスペクトル測度とすれば、それに応じて連続１パラメタユニタリ群 { U_t }_{t ∈R} が上のように定まることになるが、v を H の定義域に属す単位ヴェクトルとして、写像 Ψ を

Ψ (t ) = U_tv

として定義すれば、Ψ は微分可能であり、件の方程式の解になっている。
　要するに、系 S の状態の時間発展は、{ U_t }_{t ∈R} を S のハミルトニアン H から定まる連続１パラメタユニタリ群、v を時刻 0 ――適宜設定される時間軸の原点――における状態ヴェクトルとすれば、t を U_tv に対応づける写像よって表わされる。また、S の状態が H 上の密度作用素によって表わされる場合には、その時間発展は、D を時刻 0 における S の状態を表わす密度作用素とすれば、t を U_tDU_t^-1 に対応づける写像によって表わされる。どちらにしても、時刻 0 における状態が特定されれば、残りの状態はこれらの写像によって凡て定まる訳で、その意味で、量子力学においても系の状態は因果的に発展すると云われる。

　つづいて、量子力学において測定について云える最小限のことがらとして、ギビンズは標準的な確率解釈に言及しているのだが、１９０ページ目には次のようなくだりがある。

　ある量子系 S が状態 |> にあるとする。状態ベクトル |> を基本ベクトル |a_i > において表す。これはオブサーバブル A に対応するオペレーターの固有状態である。したがって、

|> = c_i |a_i >

ただし、Σ_i |c_i |² = 1。
　状態ベクトルの確率解釈によると、A の測定をすれば、確率 |c_i |² をもつ値 a_i の一つが与えられるであろう。A の値は確定的に a_k であるという結果が得られるであろう。その値は、|> = |a_k > である場合にのみ 1 である。

　原文は次の通り。

　 Suppose a quantum system S is in the state |>. Represent the state-vector |> in the basis |a_i > which are the eigenstates of the operator A corresponding to the observable A, so that

|> = c_i |a_i >

where Σ_i |c_i |² = 1.
　 The probability interpretation of the state-vector tells us that, idealizing a bit, a measurement of A will give one of the values a_i each with probability |c_i |². You will get the result that the value of A is a_k with certainty, which is with probability equal to 1, if and only if

|> = |a_k >. (p.104)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　量子系 S が状態 |> にあるとする。オブサーヴァブル A に対応する作用素 A の固有状態である基底 |a_i > によって状態ヴェクトル |> を表わせば

|> = Σ_i c_i |a_i >

ただし、Σ_i |c_i |² = 1。
　状態ヴェクトルの確率解釈によると、やや理想化すれば、A の測定は a_i のうちのひとつの値を、それぞれ確率 |c_i |² でもたらす。A の値が、確実に、つまり確率 1 で a_k とでるのは

|> = |a_k >

となる場合であり、その場合に限る。

　この記述は舌足らずなので補っておくと、系 S に結び付けられているヒルベルト空間 H が有限 n 次元だとすれば、以前に触れておいたように、オブサーヴァブル A に対応する自己随伴作用素 A は 1 以上 n 以下の m 箇の固有値 a₁, . . . , a_m をもち、（i ≦m となるそれぞれの正整数 i に対して）P_i を a_i に対応する固有空間 L_i を値域とする射影作用素とすれば、次が成り立つ。

A = Σ_i a_i P_i

特に m = n ならば L_i は一次元部分空間であり、v_i を L_i に属す単位ヴェクトルとすれば、{v_i }_i は H の正規直交基底を成し、H のどんなヴェクトル v についても次が成り立つ。

v = Σ_i <v_i , v >v_i ,　　 P_i v = <v_i , v >v_i

また、|a_i > = v_i 、|> = v として、ディラック表記を採れば、

v = Σ_i <a_i |>|a_i >,　　 P_i = |a_i ><a_i |

となり、次が成り立つ。

||P_i v ||² = <P_i v, P_i v > = <v, P_i v > = <|a_i ><a_i |> = |<a_i |>|²

したがって、|> が単位ヴェクトルならば、それによって表わされる状態にある S について A を測定した結果が a_i となる確率は |<a_i |>|² に等しい。（ちなみに、この場合、H のどんなヴェクトル v についても

||v ||² = ||Σ_i <v_i , v >v_i ||² = Σ_i ||<v_i , v >v_i ||² = Σ_i ||P_i v ||²
<v, Av > = <v, Σ_i a_i P_i v > = Σ_i a_i <v, P_i v > = Σ_i a_i ||P_i v ||²

となるから、v が単位ヴェクトルならば、<v, Av > が通常の期待値の定義に確かに適っているのが見てとれる。）なお、H が可算無限次元の場合にも、自己随伴作用素 A が連続スペクトルをもたず、可算無限箇の固有値をもち、それらに対応する固有空間が凡て一次元であれば、同様のことが成り立つ。

　１９１から１９２ページ目にかけては次のようなくだりがある。

　まず第１に、測定の一側面が、ある不変の巨視的な結果の記録を生みだすことにあるならば――また、そうであると考えられるならば――、相互作用はなんらかの点で巨視的な装置を含むであろう。どんな測定プロセスも、なんらかの巨視的な測定装置が不可逆的に固定されて終了し、そこにはあるオブザーバブルの値の記録が含まれていると考えられるであろう。
　第２に、系 S の A 値の測定には、S とのなんらかの物理的相互作用が必ず含まれる。ただしこの相互作用が S を擾乱する必要はない、つまり S を新しい状態へと投企する必要はない。たとえ測定装置を新しい状態へと投企しうるとしてもである。
　われわれが A 測定と呼ぶものは、ある測定装置が被測定系とつぎのような仕方で相互作用するように構成されたものである。すなわち、系 S の A 値が装置に記録される、あるいはもっと間接的にいえば、・ ・ ・ S の A 値が装置の振舞いから推定することができる。 ・ ・ ・ 　系と測定装置との相互作用が、まさに測定が直ちに繰り返されたときに同じ結果を生むケースにある測定のことをいうのならば、測定というようなものは存在しないのかもしれない。しかし、われわれにとっては幸運にも存在する。つまり、そのような測定に非常に近似する測定が存在するという経験的な事実として、測定はあると考えることができるのである。

　原文は次の通り。

　 First of all, if one aspect of a measurement is the production of some permanent macroscopic record of the result, and one would expect that it would be, then the interaction will involve a macroscopic apparatus at some point. One would expect that any measuring process would terminate in the irreversible fixing of some macroscopic measuring apparatus and that this should contain a record of the value of some observable.
　 Second, a measurement of A-value of a system S will necessarily involve some physical interaction with S, although this interaction need not disturb S, need not throw S into a new state, even though it can be expected to throw the measuring apparatus into a new state.
　 In what we might call an A-measurement we set up some measureing apparatus which interacts with the measured system in such a way that the A-value of the system S is registered on the apparatus, or, less directly, in such a way that the A-value of S can be inferred from the behaviour of the apparatus. . . . 　 If an interaction between a system and a mesuring device is a measurement just in cases where it produces the same result when repeated immediately, then there may be no such things as measurments. But luckily for us, there are. We can take as an empirical fact that to a good approximation there are such measurements. (p.104f.)

　これは次のような意味だろう。

　第一に、測定の局面のひとつが、その結果の永もちする巨視的な記録をもたらすものならば、また、そうした局面の存在は一般に要請されることだろうが、すると、測定の相互作用は何処かで巨視的な装置を巻き込むはずだ。どんな測定過程も、何らかの巨視的な測定装置が不可逆的に落ち着いて終わること、そして、そこには何らかのオブザーヴァブルの値が記録されていることが一般に期待されるだろう。
　第二に、系 S の［オブザーヴァブル］A の値の測定は、必然的に S との何らかの物理的相互作用を伴なうはずだ。ただし、その相互作用が S を攪乱し新たな状態に遷すとは限らない。仮令それが測定装置を新たな状態に遷すはずだとしても。
　何らかの測定装置が、測定の対象である系 S の A の値がそこに記録されるように S と相互作用するか、または、その挙動から件の値が間接的に推定できるように S と相互作用するよう仕組まれているとき、その装置による測定を A 測定と呼ぶことにしよう。 ・ ・ ・ 　系と測定器の相互作用が測定なのは、それが間を置かずに繰り返されれば同じ結果をもたらす場合に他ならないとすれば、測定など存在しなくてもおかしくはない。しかし、うまい具合に、そうした測定が十分な近似において存在することは経験的事実だと考えられる。

　こうして測定概念が或る程度規定されたところで、話はこの章のタイトルにもなっている射影公準に関することがらに入る。
　繰り返し実行可能な測定で、その二度の実行を隔てる時間がゼロに近づけば近づくほどそれらによって得られる値の差もゼロに近づくようなものは、理想的測定とか第一種測定と呼ばれるが、上の例のオブザーヴァブル A に理想的測定が在るとすれば、その二度の実行は、（A のとり得る値は n 箇しかないのだから）それらを隔てる時間が適当なだけ短ければ、同じ値をもたらすことになる。そこで、それらの実行結果が、例えば、共に a₁ だった場合を考えてみると、標準的解釈によれば、（A の測定結果が確実に a_k となるのは系 S の状態ヴェクトルが |a_k > の場合かつその場合だけだから）一度目の測定直後の S の状態ヴェクトルは |a₁> だったことになる。一方、一度目の測定直前の状態ヴェクトルはもちろん |a₁> とは限らない訳で、例えば、それが (1/2)|a₁> + (1/2)|a₂> だと判っていたとすれば、この状態ヴェクトルは件の測定の間に |a₁> に換わったことになるが、一度目の測定で a₁ が得られる確率は 1/2 だから、それが |a₁> に換わる確率も 1/2 だったことになる。射影公準はこのことを一般化した法則だと云える。
　一般に、量子系 S に結びつけられるヒルベルト空間 H の上には、以前に触れておいたように、オブザーヴァブル O を表わす自己随伴作用素 opO およびボレル集合 Δ に対応して射影作用素 P_opO(Δ ) が在って、密度作用素を用いる確率解釈によれば、密度作用素 D によって表わされる状態にある S について O を測定した結果の値が Δ に収まる確率は trace(DP_opO(Δ )) に等しい訳だが、射影公準によれば、O の値が Δ に収まるか否かの理想的測定は、P_opO(Δ ) の値域が有限次元であれば、S の状態を、trace(DP_opO(Δ )) に等しい確率で、(1/trace(P_opO(Δ )))P_opO(Δ ) によって表わされる状態に変える。
　例えば、上の例における測定が、A の値が a₁ であるか否かを求めるようなものだとして、系 S が密度作用素 D によって表わされる状態にあるとすれば、射影公準によれば、D は測定によって |a₁><a₁| か (1/trace(Σ _{1＜i ≦n} |a_i ><a_i |))Σ _{1＜i ≦n} |a_i ><a_i | のどちらかに変換される。それに対して、A のとり得る n 箇の値のうちの何れかが確実に得られるような測定は、D を |a₁><a₁|, . . . , |a_n ><a_n | の何れかに変換する。
　ところで、この最後の例のような、その実行によって対象とするオブザーヴァブルの値が確定する測定は極大測定と呼ばれ、そうでない測定は非極大測定と呼ばれるが、射影公準は、非極大測定に適用されると、直観に反する変換をもたらすことがある。それは、この法則が測定直前の密度作用素に関わりなく直後の密度作用素を指定するからで、ギビンズはその辺のことをいわゆるスピン 1 の系の例で説明している。
　スピン 1 の系のスピンの成分は、どんな方向についても、 を単位として 1、0、-1 の何れかの値しかとり得ず、標準的な内積を伴なう三次元複素内積空間 C³ 上の自己随伴作用素によって表わせる。そこで、S_z を z 方向についてのスピン成分を表わす作用素として、|1>、|2>、|3> を S_z の固有値 1、0、-1 にそれぞれ対応する固有ヴェクトルとすれば、これらは C³ の正規直交基底を成し、

Sz	=	|1><1| - |3><3|
（	=	1|1><1| + 0|2><2| - 1|3><3| ）

となる。ギビンズが挙げている例は、z スピンの値が { 1, 0 } に属すか否かを求める非極大な理想的測定だ。この測定を

D = λ₁|1><1| + λ₂|2><2| + λ₃|3><3|
ただし λ₁, λ₂, λ₃ ≧ 0、λ₁ + λ₂ + λ₃ = 1

となるような密度作用素 D によって表わされるアンサンブルに対しておこなった結果が { 1, 0 } に収まる確率は trace(D (|1><1| + |2><2|))、そうでない確率は trace(D |3><3|) であり、trace(|1><1| + |2><2|) = 2、trace(|3><3|) = 1 となるから、射影公準によれば、件のアンサンブルは、測定直後には、trace(D (|1><1| + |2><2|)) ： trace(D |3><3|) の比率で、密度作用素 (1/2)|1><1| + (1/2)|2><2| によって表わされる部分アンサンブルと射影作用素 |3><3| によって表わされる純粋部分アンサンブルに分かれることになる。射影公準は一般に混合の重みを保存せずランダマイズしてしまう訳だ。それだけではない。|> を

|> = c₁|1> + c₂|2> + c₃|3>
ただし |c₁|² + |c₂|² + |c₃|² = 1

となるようなヴェクトルとして、射影作用素 |><| によって表わされる純粋アンサンブルについて同じ測定をおこなったすると、射影公準によれば、このアンサンブルもまた (1/2)|1><1| + (1/2)|2><2| と |3><3| の部分アンサンブルに（比率こそ違え）分かれてしまうことになる。１９６ページ目には次のようなくだりがある。

われわれが望む状態ベクトルは、二つの純粋要素アンサンブルの混合状態として取りだしたあとに、上記に現れたような密度オペレーター ρ = |><| で記述される純粋アンサンブルのような状態ベクトルである。フィルターを「イエス」で通過する純粋な要素アンサンブルは新しい密度オペレーター、

ρ' = |>_new<|_new

をもつ。そのさい、それは c₁ と c₂ に比例して新しい状態ベクトル |>_new における |1> と |2> についての係数をもっている。 ・ ・ ・ 　フォン・ノイマン版の射影公準は、たとえそれが非極大測定に失敗するとしても、極大測定を扱っている。状態ベクトルを射影作用素に対応する状態ベクトルに射影するときに、つまり純粋アンサンブルを純粋（要素）アンサンブルに変え、混合状態から純粋要素アンサンブルを引きだすときに期待されるような測定を扱っているのである。

　原文は次の通り。

We want a state-vector like a pure ensemble described by the density operator

ρ = |><|

above to come out, after filtering, as a mixture of two pure subensembles. The pure subensembles which passes filter with ‘yes’ should have the new density operator

ρ' = |>_new<|_new

with coefficients for |1> and |2> in the new state-vector |>_new in proportion to c₁ and c₂. In other words, we want a minimally disturbed state-vector as a result. . . . 　 Von Neumann's version of the projection postulate, even if it fails with nonmaximal measurements, handles maximal measurements as one would expect, projecting state-vectors on to the state-vector corresponding to the projection operator, turning pure ensembles into pure (sub)ensembles and extracting pure subensembles from mixtures. (p.108)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

密度作用素

ρ = |><|

によって記述される純粋アンサンブルは、［測定による］フィルタリングの後には、ふたつの純粋部分アンサンブルの混合に変わるものと期待される。フィルター［の役目を果たす測定器］を「イエス」で通る純粋部分アンサンブルの新たな状態ヴェクトル |>_new は c₂ と c₂ に比例する係数を伴なった |1> と |2> の重ね合わせのはずであり、したがって、新たな密度作用素は

ρ' = |>_new<|_new

となるはずだ。 ・ ・ ・ 　フォン・ノイマン流の射影公準は、非極大測定に関しては役に立たないものの、極大測定を一般に期待されるであろう通りに扱い、状態ヴェクトルを当の射影作用素に対応する状態ヴェクトルに射影し、純粋アンサンブルを純粋（部分）アンサンブルに変え、混合から純粋部分アンサンブルを取り出す。

　非極大な理想的測定についても直観に適った変換をもたらすのが、リューダースの規則と呼ばれる射影公準の改良ヴァージョンだ。前と同じく P_opO(Δ ) をオブザーヴァブル O を表わす自己随伴作用素 opO およびボレル集合 Δ に対応する射影作用素とすれば、リューダースの規則によれば、密度作用素 D によって表わされる状態にある系 S の O の値が Δ に収まるか否かの理想的測定は、S の状態を、trace(DP_opO(Δ )) に等しい確率で、(1/trace(DP_opO(Δ )))P_opO(Δ )DP_opO(Δ ) によって表わされる状態に変える。
　これを上の例に適用すれば、密度作用素 λ₁|1><1| + λ₂|2><2| + λ₃|3><3| によって表わされるアンサンブルは、測定直後には、密度作用素

(λ₁/(λ₁+ λ₂))|1><1| + (λ₂/(λ₁+ λ₂))|2><2|

によって表わされる部分アンサンブルと射影作用素 |3><3| によって表わされる純粋部分アンサンブルに分かれ、単位ヴェクトル |>（= c₁|1> + c₂|2> + c₃|3>）が属す一次元部分空間を値域とする射影作用素 |><| によって表わされる純粋アンサンブルは、射影作用素

		(1/(|c1|2 + |c2|2))(|c1|2|1><1| + c1c2*|1><2| + c1*c2|2><1| + |c2|2|2><2|)
（	=	(1/(|<1|>|2 + |<2|>|2))(|<1|>|2|1><1| + <1|><|2>|1><2| + <|1><2|>|2><1| + |<2|>|2|2><2|)
	=	(1/trace(|><|(|1><1| + |2><2|)))((|1><1| + |2><2|)|><|(|1><1| + |2><2|)) ）

によって表わされる純粋部分アンサンブルと |3><3| によって表わされる純粋部分アンサンブルに分かれることになる。(1/(|c₁|² + |c₂|²))(|c₁|²|1><1| + c₁c₂^*|1><2| + c₁^*c₂|2><1| + |c₂|²|2><2|) の値域は単位ヴェクトル (c₁/(|c₁|² + |c₂|²))|1> + (c₂/(|c₁|² + |c₂|²))|2> が属す一次元部分空間だ。１９７から１９８ページ目にかけては次のようなくだりがある。

　したがって、われわれはここに２種類の射影公準をもつのである。どちらも単純に正しくも誤りでもない。どちらも測定が無作為化するか否かによって決まる、ある与えられた測定に対して適切か適切でないかするのである。・ ・ ・
　これまでにわれわれがしてきたことのすべては、量子力学には二通りのプロセスがあるという困惑させる事実を記述することである。それは測定と非測定であり、２種類の射影公準が存在するという事実と同じことである。２種類の射影公準は、測定がシュレーディンガー方程式から生む偏差の二通りの説明である。なにが測定と非測定との違いについて説明するのかをわれわれは知らない。

　原文は次の通り。

　 So here we have two versions of the projection postulate. Neither is simply right or wrong. Each is suitable or unsuitable for a given measurement depending on whether that measurement is randomizing or not. . . .
　 So far all we are doing is describing the puzzling fact that in quantum mechanics there are two kinds of process, measurments and nonmeasurements, a fact not to be confused with there being two versions of the projection postulate. The two versions of the projection postulate are two accounts of the deviation that measurement makes from Schrödinger's equation. We don't know what accounts for the difference between measurments and nonmeasurements. (p.109)

　これは次のような意味だろう。

　そんな訳で、我々は射影公準のふたつのヴァージョンを手にしている。どちらも単純に正しくもなければ誤りでもなく、それらの適不適は当該の測定がランダマイジングなものであるか否かにかかっている。・ ・ ・
　これまでして来たのは、量子力学には測定と非測定という二種類のプロセスが在るという当惑させられる事実の記述であり、この事実を射影公準のふたつのヴァージョンの存在と混同してはならない。射影公準のふたつのヴァージョンは、測定がもたらすシュレーディンガー方程式からの逸脱の二通りの説明だ。測定と非測定の違いが何に由るのかを我々は知らない。

　ここでもうひとつ注意しておきたいのは、測定がアンサンブルをランダマイズすると云っても、依然それは理想的測定に関する話なのであって、ランダマイジングな測定も、それが間を置かずに繰り返されれば、同じ値をもたらすものとされているということだ。
　つづいての話題はフォン・ノイマンの測定の理論だ。１９８から１９９ページ目にかけては次のようなくだりがある。

しかし、射影がいかに起こるのかをわれわれは知らない。あるいは、射影が起こったとしても、量子力学が測定プロセスを正しく記述できるかどうかさえ、われわれは知らないのである。
　測定の量子論における根本的な問いはこうである。測定というものが一体ありうるのか？ もう一つの根本的な問いはこうである。測定というものがあるべきなのか？ ・ ・ ・
　おそらくフォン・ノイマンの理論は、そのような理論が満たすべき諸条件についての一連の諸成果に鑑みると、測定の理論になっているとはいえない。しかし、それらの諸成果はそれ自身のパズルを生み、量子力学の哲学が測定問題と呼ぶものの焦点となっている。ゆえに、この限定された意味においては、測定の量子論が確かにありうる。
　フォン・ノイマンは手始めに、われわれは被測定系 S と測定装置 M のどちらをも量子力学のフォーマリズムによって記述することができると仮定する。・ ・ ・ われわれはこう問う。M と S の相互作用を一つの測定たらしめるものはなにか？
　ミニマルな解答はこうである。S が測定相互作用のあとにどんな状態にあっても、M は S と相関しているに違いない結果を記録する。M によって記録されたその結果はこの状態を呈示しなければならず、さもなければ相互作用はあるのであろうが、測定というものはない。

　原文は次の通り。

However, we do know how the projection takes place, or even whether quantum mechanics can properly describe the measurement process, given that a projection does takes place.
　 The fundamental issue in the quantum theory of measurement is: can there be one? Another funfdamental issue is: should there be one? . . .
　 Von Neumann's is perhaps less a theory of measurement than a set of results about the conditions such a theory must satisfy. However, these results generate puzzles of their own and are the focus of what philosophers of quantm mechanics call the measurement problem. In this limited sense then there certainly can be a quantum theory of measurement.
　 Von Neumann begins by supposing that we can describe both the measured system S and the measurering apparatus M via the formalism of quantm mechanics. . . . We ask: what makes the interaction of M and S a measurement?
　 The minimal answer is that M registers a result which must be correlated with whatever state S has after the measurement interaction. The result registered by M must reveal this state, otherwise there would be an interaction but no measurement. (p.109f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

しかし、どうして射影が起こるのか、あるいは、それが確かに起こるとしても、量子力学が測定過程をまともに記述できるのかどうかさえ、我々は知らない。
　測定の量子論に関する根本的な争点は、測定の量子論は存在し得るのかということであり、さらなる根本的な争点は、それは存在すべきなのかということだ。・ ・ ・
　フォン・ノイマンの理論は、測定の理論と呼ぶには足りず、そうした理論が充たすべき条件をめぐる結論の集合に過ぎないかも知れない。しかし、それらの結論は、固有のパズルを惹き起こすため、量子力学の哲学者たちが測定問題と呼ぶものの焦点となっている。この限られた意味でならば、測定の量子論は確かに存在し得る。
　フォン・ノイマンは、測定の対象である系 S も測定装置 M も量子力学のフォーマリズムによって記述できるものと仮定することからはじめている。・ ・ ・ 問題は、何が M と S の相互作用を測定たらしめるのかだ。
　最小限の答は、その相互作用の結果を M が記録すること、そして、件の結果はその相互作用後の S の状態に相関したものであること、というものだ。M に記録されたその結果が件の状態を明らかにするのでなければ、相互作用はあっても測定があったことにはならないだろう。

　ギビンズが焦点を合わせているのは、フォン・ノイマンがその著書『量子力学の数学的基礎』の最後の辺で展開している極大な理想的測定についての数学的考察らしい。そこで扱われているのはオブザーヴァブルのとり得る値が可算無限箇のケースだが、ここでは、話を簡単にするために、系 S に対応するヒルベルト空間 H₁ は有限 n 次元で、S のオブザーヴァブル A を表わす自己随伴作用素 A は n 箇の固有値 a₀, . . . , a_{n -1} をもつものとして、|S, i > を a_i に対応する固有空間に属す単位ヴェクトルとする。（よって、{ |S, i > }_i は H₁ の正規直交基底であり、A = Σ_i a_i |S, i ><S, i |。）そこで、測定装置 M による S の A の極大な理想的測定を考えれば、その実行によって M は a₀, . . . , a_{n -1} の何れかを記録するはずだが、a_k を記録した M の状態は n 次元ヒルベルト空間 H₂ の正規直交基底 { |M, i > }_i に属すヴェクトル |M, k > によって表わせるものとする。（したがって、S と M は、測定直前の S の状態ヴェクトルが |S, k > ならば測定後の M の状態ヴェクトルは |M, k > に換わるように相関していることになる。）さらに、S と M の結合系 S + M の状態はテンソル積ヒルベルト空間 H₁ H₂ のヴェクトルによって表わせるものとして、測定直前の S と M の状態ヴェクトルをそれぞれ |S, k > および |M, j > とすれば、S + M の状態ヴェクトルは |S, k >|M, j > であり、これは、測定によって |S, k >|M, k > に換わることになる。（このように抽象的に考えている限り S + M のハミルトニアンの具体的な形は問い得ない訳だが、ともあれ、そうした変換をもたらす H₁ H₂ 上のユニタリ作用素は存在する。i を n で割った余りを「r (i )」と表わすことにして、H₁ H₂ のヴェクトル Σ_i Σ_m c_i,m |S, i >|M, m > を Σ_i Σ_m c_i,m |S, i >|M, r (m + i )> に対応づける写像を考えれば、これはユニタリ作用素であり、|S, k >|M, 0> を |S, k >|M, k > に変換する。）１９９から２００ページ目にかけては次のようなくだりがある。

言い換えれば、装置は状態 j から状態 k へと展開し、S は状態 k にある（そしてたまたまあった）という結果を呈示するのである。ハミルトニアンが存在して、S を擾乱せずに M を変えるというこの効果を生む S と M との結合状態を記述することは、フォン・ノイマンの理論から帰結する。量 A を測定する方法は、S と選ばれた M との相互作用を構成するというやり方であり、その方法が M のこうした展開を生みだすのである。
　より一般的なケースは、S が初期に、測定されるオブザーバブル A の固有状態にない場合であるが、こちらのほうがより興味深い。当然、S はどんな状態にあっても、|S, k > の重ね合わせとして表すことができる。つまり、M が測定するオブザーバブルの固有状態として表すことができる。それゆえに、S は初期につぎのような状態にあるだろう。

|S > = Σ_ck|S, k >

ただし、Σ_k |c_k |² = 1。
　線形性によってさきの理論が適用するので、今度の場合、つぎのように展開する。

(Σ_ck|S, k >) |M, j > Σ_ck|S, k > |M, k >

　言い換えれば、結合系 S + M は、個々のヒルベルト空間のテンソル積における状態ベクトルによって表される状態で相互作用を終えるのである。S と M それぞれの観点からすれば、これはおかしな状態である。S も M もそれぞれの状態をもっているとはいえない。S も M もそれぞれ状態の重ね合わせにはない。測定装置 M は確かに決定状態にはない。それでもわれわれはいつでも測定を行うし、測定装置はつねに決定的であることがわかる。こうした結果はいかにして和解させることができるか？ ・ ・ ・
　われわれはそれらを和解させることができない、というのがフォン・ノイマンの解答である。かれは量子系が受けうる二通りの展開を区別する。第１のプロセスでは、変化は不連続的であり、シュレーディンガー方程式を破る。反対に、第２のプロセスはシュレーディンガー方程式に支配されており、その方程式が引き起こす状態の変化は連続的である。フォン・ノイマンはまた、単純ではあるが重要な「一貫性ある」結果を証明している。すなわち、もう一つの測定系が最初の測定系と相互作用し、最初の装置によって示される S の力学的変数の値を測定しても、第２の系によって示される結果は、最初の装置によって記録される結果と一致することを証明をしているのである。そのプロセスは無限に反復可能である。

　原文は次の通り。

　 In other words, the apparatus evolves from state j to the state k exhibiting the result that S is (and was as it happens) in the state k. That there are Hamiltonians describing couplings between S and M which create this effect, of changing M without disturbing S, follows from von Neumann's theory. The art of measurering the quantity A is the art of constructng interactions between S and the chosen M which generate this evolution of M.
　 The more general case, when S is initially not in an eigenstate of the measured observable A, is the more interesting. One can naturally represent whatever state S is in as a superposition of the states |S, k >, the eigenstates of the observable that M measures. The measured system S will therefore initially be in the state

|S > = Σ_k c_k |S, k >

where Σ_k |c_k |² = 1.
　 By the linearity the previous theory applies, so that the evolution is this time

(Σ_k c_k |S, k >) |M, j > → Σ_k (c_k |S, k > |M, k >).

　 In other words, the combined system S + M finish the interaction in a state represented by a state-vector in the tensor product of their individual Hilbert space. From the point of view of S and M separately this is a funny state. Neither S nor M can be said to have its own state. Neither S nor M is separately a superposition of states. Yet we make mesurements all the time and find that the measuring apparatus is always determinate. How can we reconcile these results . . . ?
　 Von Neumann's answer is that we cannot reconcile them.
　 He distinguishes between two kinds of evolution a quantum system can undergo. In processes of the first kind the change is discontinuous and in violation of Schrödinger's equation. By contrast processes of the second are governed by Schrödinger's equation and the changes of state they induce are continuous. Von Neumann also proves a simple but important ‘consistency’ result, namely that if a further measuring system interacts with the first measuring system and measures the value of the dynamical variable of S displayed by the first apparatus the result displayed by the second system will be consistent with that registered by the first apparatus. The process can be iterated ad infinitum. (p.110f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　云い換えれば、件の装置は、状態 j から状態 k へと発展し、（この場合もともと状態 k にあった）S が状態 k にあるという結果を提示する。このように S を攪乱することなく M に変化をもたらす S と M の結合を記述するハミルトニアンが存在することは、フォン・ノイマンの理論から帰結する。量 A を測定することは、そうした発展を適当な M に惹き起こす S と M の相互作用を仕組むことだ。
　より興味深いのは、S のはじめの状態がオブザーヴァブル A の固有状態ではない一般的なケースだ。S のどんな状態も A の固有状態 |S, i >［つまり |S, 0>, . . . , |S, n -1>］の重ね合わせとして表わせる訳だから、S のはじめの状態は次のようになる。

|S > = Σ_k c_k |S, k >

ただし Σ_k |c_k |² = 1。
　先のことを線形性によって当てはめれば、発展は今度は次の通り。

(Σ_k c_k |S, k >)|M, j > → Σ_k c_k |S, k >|M, k >

　云い換えれば、結合系 S + M は、それぞれのヒルベルト空間のテンソル積に属す状態ヴェクトルによって表わされる状態で相互作用を終える。S と M を別々に見れば、これは妙な状態だ。S も M もそれ自体の状態をもっているとは云えない。S も M も個々には重ね合わせ状態にはない。にもかかわらず、測定は始終おこなわれ、測定装置はいつでも確定的なことが見出される。どうすればこれらのことがらを調停できるか？ ・ ・ ・
　調停できないというのがフォン・ノイマンの答だ。彼は量子系が被り得る発展を二種類に分けている。その第一種のプロセスにおいては、系の状態の変化は非連続的でシュレーディンガー方程式に従わない。対照的に、第二種のプロセスはシュレーディンガー方程式に規定され、それによって惹き起こされる変化は連続的だ。フォン・ノイマンは、また、単純だが重要な「整合性」、つまり、さらに別の測定系が第一の測定系と相互作用し、第一の装置に表示される S の力学的変数の値を測定したとしても、第二の系によって表示される結果は、第一の装置によって記録された結果と整合的なはずであることを証明している。この過程は際限なく反復可能だ。

　Σ_k c_k |S, k >|M, k > は、(Σ_k c_k |S, k >)|M, j > と違って、S と M それぞれの状態ヴェクトルを単純に並べた形にはなっておらず、また、そうした形に変形することもできない。したがって、S にも M にも個別には状態ヴェクトルを帰し得ない。（これは、第六章で「凡ての交差項の係数がゼロ」と表現されている相関系に特有の状態ヴェクトルの一例だ。）しかし、それらを全く別々に扱えない訳ではなくて、どちらをとっても同様だから S についてだけ云えば、以前に触れておいたように、H₁ H₂ 上の密度作用素 D には、その「リダクション」と呼ばれる H₁ 上の密度作用素 D₁ がひとつだけ在って、H₁ 上のどんな自己随伴作用素 B についても

trace₁(D₁B ) = trace(D (B I₂ ))

となる訳だが、D によって表わされる状態にある系 S + M の部分系としての S の状態は、この D₁ によって表わされるものとされる。すると、D を単位ヴェクトル Σ_k c_k |S, k >|M, k > が属す一次元部分空間を値域とする射影作用素とすれば、そのリダクション D₁ は、

D₁ = Σ_k |c_k |²|S, k ><S, k |

となり、D によって表わされる純粋状態にある S + M の部分系としての S の状態は、混合状態であることになる。しかも、この D₁ は、密度作用素

		Σk |ck |2|S, k >|M, k ><S, k |<M, k |
（	=	Σk |ck |2|S, k ><S, k | |M, k ><M, k | ）

のリダクションでもある。一般に、D₁ と D₂ がぞれぞれ H₁ および H₂ 上の密度作用素ならば、H₁ H₂ 上には D₁ と D₂ がそのリダクションであるような密度作用素 D が存在するが、そうした D が唯ひとつに定まるのは、D₁ と D₂ の少なくともどちらかが射影作用素である場合であり、その場合に限る。（なお、「極大測定」や「理想的測定」や「射影公準」といった術語はフォン・ノイマンのものではないことを付け加えておく。）
　２０３から２０４ページ目にかけては次のようなくだりがある。

　第１種のプロセスが複数あることを否定し ・ ・ ・ 決定論を保持するもう一つの方法がある。一般的に、あるオブザーバブルの測定とは純粋状態を混合状態へと変えることである。・ ・ ・ しかし、純粋状態から混合状態への変換は本当には起こらず、ただ起こるようにみえるものと仮定せよ。連続的に発展する純粋状態と混合状態とが、すべての巨視的なオブザーバブルに対して同じ期待値をとるとしても、統計的に等しいことは示しえないと仮定せよ。ゆえに、測定において波束の崩壊に訴える理由は、便宜上という以外にはないと論ずることができる。
　デイネリ、ロワンジェ、およびプロスペリは、熱力学的な測定の理論において、重ね合わせと混合状態とが、巨視的系に適用する巨視的オブザーバブルに対して統計的に等しいことを示した。・ ・ ・ そしてこのことは、一時のナンシー・カートライトのようなある哲学者たちにとって、シュレーディンガー方程式が普遍的に真であることを望む実在論者に一撃を食らわす方法を提出しているように思われた。・ ・ ・ もちろん、このことすべてがアンサンブル解釈にとってだけ慰めとなりうるわけではない。量子力学を個別の系に適用すべきものと考えれば、干渉項が通常の仕方で現れてくることが期待できるのである。
　しかし、重ね合わせと混合状態との統計的等価性は、アンサンブル内の個々の状態の振舞いが等価であることを保証するのではない。

　原文は次の通り。

　 There is a way of denying that there are processes of the first kind and retaining determinism. . . . In general the measurement of an observable will transform a pure state into a mixture. . . . But suppose that this change of a pure state into a mixture does not really happen but only appears to happen. Suppose that it could be shown that a continuously evolving pure state and the mixture are statistically equivalent, giving the same expectation values for all macroscopic observables. Then one could argue that there is no reason, other than convenience, for appealing to the collapse of the wave-packet in measurement.
　 Daneri, Loinger, and Prosperi, in their thermodynamic theory of measurement, showed that superposotion and mixture are statistically equivalent for macroscopic observables applying to macroscopic systems. . . . This seemed to some philosophers, like Nancy Cartwright at one time, to offer a way out for the realist who wanted the universal truth of Schrödinger's equation. . . . Of course all this can be of comfort only to an ensemble interpretation. If you take quantum mechanics to apply to the individual system you can expect the interference terms to be show up in the usual way.
　 However the statistical equivalence of superposition and mixture does not guarantee that the behaviour of individuals in the ensemble will be equivalent. (p.112f.)

　これは次のような意味だろう。

　第一種のプロセスの存在を否定し ・ ・ ・ 決定論を維持する方途は在る。一般に、オブザーヴァブルの測定は純粋状態を混合状態に換えるはずだ。・ ・ ・ しかし、この純粋状態から混合状態への変換は、本当に起こる訳でなく、ただ起こるようにみえるだけだと考えてみよう。連続的に発展する純粋状態と混合状態は凡ての巨視的オブザーヴァブルについて同一の期待値をもたらし統計的に同等だということが示せたとすれば、測定において波束の崩壊［つまり射影］に訴える理由は便宜上の他には無いと主張できるだろう。
　ダネリとロインゲルとプロスペリは、彼らの測定の熱力学的理論において、巨視的系に当てはまる巨視的オブザーヴァブルに関しては、重ね合わせと混合が統計的に同等であることを示した。・ ・ ・ ひところのナンシー・カートライトのような哲学者には、これがシュレーディンガー方程式の普遍的な正しさを求める実在論者の突破口 となるかに見えた。・ ・ ・ もちろん、以上のことがらはただアンサンブル解釈の慰めとなり得るに過ぎない。量子力学は個別の系に当てはまるものと考えれば、干渉項が例の如く顔を出すことになるはずだ。
　ところが、重ね合わせと混合の統計的同等性は、アンサンブル内の個々の系の振舞が同等であることを保証しない。

　すぐ上の極大な理想的測定の例で、|> を A の固有ヴェクトルではない状態ヴェクトルで

|> = Σ_i c_i |S, i >

となるようなものとすれば、|> は件の測定によって |c_k |² の確率で |S, k > に変換されることになるが、これは、古典論的な統計的観点からは、|> によって表わされる系からなる純粋アンサンブルが密度作用素 Σ_i |c_i |²|S, i ><S, i | によって表わされるアンサンブルに変わることを意味していると考えられる。ところで、オブザーヴァブル A だけを考えている限り、|> に対応するアンサンブルと Σ_i |c_i |²|S, i ><S, i | によって表わされるアンサンブルは、統計的に区別できない。|> に対する測定結果が a_k とでる確率は |c_k |² である一方、Σ_i |c_i |²|S, i ><S, i | に対する測定結果が a_k とでる確率もまた

trace((Σ_i |c_i |²|S, i ><S, i |)|S, k ><S, k |) = Σ_i |c_i |²<S, i |S, k ><S, k |S, i > = |c_k |²

となるからだ。しかし、これらふたつのアンサンブルの統計的差異は、他のオブザーヴァブルを考慮に入れれば、顕わになる。
　一般に、O と R を量子系 S のオブザーヴァブルとして、opO と opR をそれらを表わすヒルベルト空間 H 上の自己随伴作用素、{ P_opO(Δ ) }_Δ∈B と { P_opR(Δ ) }_Δ∈B をそれらに対応するスペクトル測度とすれば、O と R は、どんなボレル集合 Δ および Γ についても P_opO(Δ ) と P_opR(Γ ) が可換なとき（つまり P_opO(Δ )P_opR(Γ ) = P_opR(Γ )P_opO(Δ ) となるとき）両立可能であると云われ、そうでなければ両立不能であると云われる。（なお、O と R が両立可能であることは集合 { v ∈ H | どんなボレル集合 Δ と Γ についても P_opO(Δ )P_opR(Γ )v = P_opR(Γ )P_opO(Δ )v } が H に等しいことと同等だが、この集合がゼロヴェクトルだけからなるとき、O と R は全く両立不能であると云われる。）H が有限次元の場合、O と R が両立可能であることは opO と opR が可換であることと同等だ。
　そこで、先の例に戻って、O を A と両立不能なオブザーヴァブルとして、話を簡単にするために、O を表わす自己随伴作用素 opO は n 箇の固有値をもち

opO = Σ_i b_i |i ><i |

というようにスペクトル分解されるものとする。（この場合、O と A が両立不能であることは、非可換な |i ><i | と |S, j ><S, j | が在ることと同等だ。）すると、|> に対する O の測定結果が b_k とでる確率は

<|k ><k |> = Σ_i Σ_j c_i^*c_j <S, i |k ><k |S, j >

となる一方、Σ_i |c_i |²|S, i ><S, i | に対する O の測定結果が b_k とでる確率は

Σ_i |c_i |²<S, i |k ><k |S, i >

であり、それらの差

Σ_i Σ_j c_i^*c_j <S, i |k ><k |S, j > - Σ_i |c_i |²<S, i |k ><k |S, i >

は一般に 0 ではない。（「干渉項」とはこの差のことだ。）
　ところが、巨視的系の巨視的オブザーヴァブルに関しては、そうした差異は消えてしまう、というのがダネリらの示したことらしい。

　この章の最後の話題は、混合状態の無知解釈だ。ギビンズは、今度は、電子ビームの例を用いている。x 方向について上向きのスピンをもつ電子からなるビームと下向きのスピンをもつ電子からなるビームを混ぜ合わせたビームだ。２０６から２０７ページ目にかけては次のようなくだりがある。

ゆえに、新しい混合状態は２本の要素ビームから成るものといいたくなるであろう。１本はその電子数のすべてが x 方向にスピン「上向き」をもち、もう１本はその電子数のすべてが x 方向にスピン「下向き」をもつ２ビームである。二つの要素アンサンブルを混合しても、それらをより大きな全体の一部にするということ以外、二つの要素アンサンブルを干渉することはない。そのアンサンブルについての密度オペレーターはつぎのようになる。

ρ = (1/2)|+x ><+x | + (1/2)|-x ><-x |

　この ρ からは、電子数の半分は x 方向にスピン「上向き」もう半分は「下向き」であり、他の方向にスピン「上向き」をもつものはない、という事実があたかも読み取れるこのようである。このことは混合状態の無知解釈から以下の点にしたがって帰結する。
　（１）　量子系がある混合状態に属することがわかっているときには、その量子系は混合状態を構成する純粋要素アンサンブルの一つに本当に属している。われわれはどちらの要素アンサンブルであるかを知っているのだが。
　（２）　密度オペレーターの表記内の係数は、一体どちらの要素サンサンブルにその量子系が属しているかについてのわれわれの知識の尺度を与える。
　混合状態の無知解釈は量子力学的アンサンブルの混合を、まさに古典的アンサンブルの混合と同じものとみなす。ゆえに、量子力学における確率は二つの成分からつくられる。一つは純粋に量子力学的で、重ね合わせの原理から帰結し、純粋アンサンブルにさえ作用する。もう一つは量子力学と古典力学のどちらにも適用可能で、つまり純粋アンサンブルを混合するということである。
　問題は、密度オペレーター ρ が他のどんな方向 δ についても、

ρ = (1/2)|+δ ><+δ | + (1/2)|-δ ><-δ |

と表せることである。したがって、混合状態の無知解釈によれば、われわれはこうも推論できるのである。すなわち、ビーム内の電子数の半分は異なる d 方向にスピン「上向き」をもち、半分は「下向き」をもつ。しかし、二つの方向に、つまり x 方向と d 方向に確定したスピンをもちうる電子は存在しない。
　混合状態の無知解釈に一撃を食らわすことが可能な一方法は、われわれは密度オペレーターから混合状態の成分を読み取るという主張（２）を降ろすことである。すると、密度オペレーターの表記は、すべてではないが等しく受け入れることができる。統計的にはすべての表記は等価であるのだが。

　原文は次の通り。

Then you will want to say that the new mixture consists of two subbeams, one with all its members having spin ‘up’ in the x -direction, and the other will be with all its members having spin ‘down’ in the x -direction. The mixing of the two subensembles does not interfere with two subensembles except to make them parts of a larger whole.
　 The density operator for the ensemble is

ρ = (1/2)|+x ><+x | + (1/2)|-x ><-x |.

　 It looks as though you can read off from ρ the fact that half the electrons have spin ‘up’ and half have spin ‘down’ in the x -direction and none has spin ‘up’ in any other direction. This follows from the ignorance interpretation of mixtures, according to which

　 (1) whenever we know that a quantum system belongs to a mixture, it really belongs to one of the pure subensembles of which the mixture is composed, though we do know which;
　 (2) the coefficients in the expression for the density operator gives us a measure of our knowledge of which subensemble it does belong to.

　 The ignorance interpretation of mixtures takes the mixing of quantum-mechanical ensembles to be just like the mixing of classical ensembles. Probability in quantum mechanics is then made up of two components, one purely quantum mechanical, a result of superposition principle and affecting even pure ensembles, the other applicable both to quantum and classical mechanics, a matter of a mixing of pure ensembles.
　 The trouble is that the density operator ρ can be represented as

ρ = (1/2)|+d ><+d | + (1/2)|-d ><-d |

for any other direction d.
　 Therefore, according to the ignorance interpretation of mixtures, we could also infer that half the electrons in the beam have spin ‘up’ and half spin ‘down’ in the different d-direction. However no electron can have determinate spins in two directions, x -direction and d-direction.
　 One possible way out for the ignorance interpretation is to drop its claim (2), that we can read off the composition of a mixture from its density operator. Thus, not all representations of the density operator may be equally acceptable, even though all are equivalent statistically. (p.114f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

そうすると、この新たな混合状態は、x 方向について「上向き」のスピンをもつ電子のビームと x 方向について「下向き」のスピンをもつ電子のビームというふたつの部分ビームから成ると云いたくなる。それらふたつのアンサンブルは、より大きなアンサンブルの部分となることを別にすれば、件の混ぜ合わせによって干渉を被ることはない。
　件のアンサンブルの密度作用素 ρ は次の通り。

ρ = (1/2)|x, +><x, +| + (1/2)|x, -><x, -|

　この ρ からは、半数の電子が x 方向について「上向き」のスピンをもち、あとの半分は「下向き」であり、他のどんな方向についても「上向き」のスピンをもつものは無いということが読み取れるかに見える。これは次のような混合状態の無知解釈から帰結する。

　（１）　量子系が或る混合状態に属すことが判っているときには、その量子系は、件の混合状態を構成する純粋部分アンサンブルのひとつに、それがどれであるかを我々は知らないにしても、実際には属している。
　（２）　その場合、対応する密度作用素の表現における係数は、その量子系がどの部分アンサンブルに属しているのかについての我々の知識の尺度となっている。

　混合状態の無知解釈は、量子力学的アンサンブルの混ぜ合わせを古典論的アンサンブルの混ぜ合わせと全く同様に扱う。よって、量子力学における確率は、重ね合わせ原理から帰結する純粋に量子力学的な、純粋アンサンブルにすら巣くう成分と、量子力学と古典力学のどちらにも当てはまる純粋アンサンブルの混ぜ合わせに関わる成分のふたつから成る。
　ところが、困ったことに、先の密度作用素 ρ は他のどんな方向 d をとっても

ρ = (1/2)|d, +><d, +| + (1/2)|d, -><d, -|

と表わせる。
　したがって、混合状態の無知解釈に従えば、件のビームの半数の電子は d 方向について「上向き」のスピンをもち、あとの半分は「下向き」のスピンをもつとも云える訳だ。しかし、x と d の二方向について確定したスピンをもつ電子など在り得ない。
　無知解釈にとり得るひとつの解決策は、密度作用素から混合状態の構成を読み取ることができるという主張（２）を棄てることだ。よって、ひとつの密度オペレーターに対する表現は、統計的には凡て同等だとしても、どれもが等しく受け容れられる訳ではない。

　電子のようなスピン 1/2 の系のスピン状態は、標準的な内積を伴なう複素ヴェクトル空間 C² の単位ヴェクトルによって表わせる訳だが、どんな方向 d をとっても、その方向について上向きおよび下向きのスピン状態をそれぞれ表わすヴェクトル |d, +> と |d, -> は C² の正規直交基底を成すから、次が成り立つ。

(1/2)(|x, +><x, +| + |x, -><x, -|) = (1/2)(|d, +><d, +| + |d, -><d, -|) = (1/2)I

（ただし I は C² 上の恒等作用素。）しかし、密度作用素の表現の多様性は、このようなケースにとどまるものではない。例えば、a を、0 ＜ a ＜ 1 かつ a ≠ 1/2 となるような実数とすれば、

a |x, +><x, +| + (1 - a )|x, -><x, -|

は密度作用素だが、これに対して、

b |1><1| + (1 - b )|2><2| = a |x, +><x, +| + (1- a )|x, -><x, -|,　　0 ＜ b ＜ 1

となるような実数 b および C² の一次元部分空間を値域とする射影作用素 |1><1| と |2><2| の三項組 { b, |1><1|, |2><2| } は、|1><1| と |2><2| それぞれの値域が直交することを求めないならば、無数に存在する。次元が 3 以上のヒルベルト空間上の密度作用素に関しても事情は同様だ。

　ここで、スピン 1/2 の系の x 、y 、z 以外の方向のスピン成分に関して簡単に触れておく。
　三次元ユークリッド空間に直交座標系 Oxyz を設定して、原点 O を中心とする半径 1 の球――いわゆる単位球――を考えれば、件の座標系に相対的な方向は、この球面上の点の座標によって表わすことができる。そこで、(x_d , y_d , z_d ) を方向 d を表わす座標で -1 ＜ z_d ＜ 1 となるものとすれば、それに対して次を充たす実数 θ と φ が唯ひとつづつ定まる。

x_d = sin(θ )cos(φ ),　　y_d = sin(θ )sin(φ ),　　z_d = cos(θ )
-π ＜ θ ≦ π,　　-π/2 ＜ φ ≦ π/2

（要するに θ と φ は点 (x_d , y_d , z_d ) のいわゆる極座標を成す。）d 方向のスピン成分を表わす自己随伴作用素 S_d および状態ヴェクトル |d, +> と |d, -> は、d に応じてこうして定まる θ と φ を用いて、次のように定義することができる。 すると、S_d のスペクトル分解は次のようになる。

*

　第八章の主題は非局所性と隠れた変数だ。
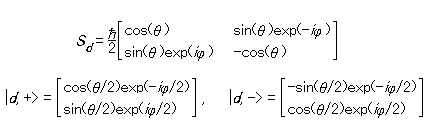
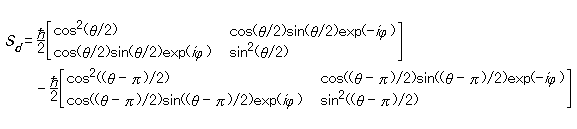
　２０９から２１２ページ目にかけては次のようなくだりがある。

局所性がとりわけ意味するところは、「遠隔作用の不在」である。局所性はまた、ある物理系の諸属性はその系のすぐ近くの事象によってのみ影響されることを意味する。さらに局所性はまた、複合した物理系は、たしかに相互作用する諸成分の集まりとして記述されるかもしれないが、その他の点では独立した諸成分の集まりとして記述されることを意味する。ゆえに非局所性とは、非局所的な諸力、つまり非局所的相関の問題、あるいは物理的全体論の問題となりうるのである。
　非局所的な諸効果、非局所的宇宙、および非局所的な諸理論について、われわれはあまり区別せずに語る。・ ・ ・ 上にあげた局所性の意味のうち、少なくとも第２、第３の意味からみた場合（それらが本当に別々の問題であるかぎり）、つまり諸力なき非局所性という意味において、量子力学は非局所的な理論である。 ・ ・ ・ 　・ ・ ・ EPR の精神は、素朴さを差しはさまずに量子力学が非局所的であるか、さもなければ不完全であることを立証する、というものである。思い起してみれば、アインシュタインは局所性が有意味な物理理論に必然的な特性であると仮定したので、量子力学の不完全性について論じたのである。もし量子力学が不完全であれば、おそらく量子力学は、より本質的な「隠れた変数」によるミクロ物理学的な状態の記述によって補足されるべきであり、量子力学的な状態は、こうしたより本質的な状態への途上にあるにすぎないと考えられるであろう。
　EPR 以後の、量子力学の哲学へのもっとも重要な貢献――ベルの不等式にかんする J. S. ベルの仕事――は、EPR の思考実験を、あるいはむしろ EPR-B の思考実験を深化し一般化することにある。

　原文は次の通り。

Locality means, among other things, ‘no action-at-a-distance’. It means that the properties of a physical system are affected only by events in the immediate vicinity of the system. It also means that complex physical systems may be described as collections of interacting, but otherwise independent, components. Nonlocality can be a matter of nonlocal forces, of nonlocal correlations, or of physical holism.
　 We speak ambiguously of nonlocal effects, a nonlocal universe, and nonlocal theories. . . . In the second and third of these senses of locality (insofar as they are really separable) ―― nonlocality without forces ―― quantum mechanics is a nolocal theory. . . . 　 . . . The genious of EPR is that it demonstrates without naivety that either quantum mechanics is nonlocal or that it is incomplete. Einstein, we recall, assumed that nonlocality was a necessary feature of any sensible physical theory and so argued for the incompleteness of quantum mechanics. If quantum mechanics is incomplete then it should presumably be supplemented with a deeper ‘hiden-variables’ description of microphysical states and one would expected that quantum-mechanical states would turn out to be mere averages over these deeper states.
　 The most important contribution to the philosophy of quantum mechanics since EPR ―― J. S. Bell's work on his inequalities ―― consists of a deepning and generalizing of the EPR, or rather the EPR-B thought-experiment. (pp.116-118)

　これは次のような意味だろう。

局所性は、とりわけ「遠隔作用の存在不能」を意味する。これは、物理系の属性は件の系のすぐ傍の出来事にだけ影響されることを意味する。それは、また、複雑な物理系は、相互作用していることを別にすれば独立した構成要素の集まりとして記述できることを意味する。非局所性は、非局所的な力に関わることがらでもあれば、非局所的相関に関わることがらでも物理的全体論に関わることがらでもあり得る。
　非局所的効果とか非局所的宇宙とか非局所的理論といった言葉を我々はあいまいに用いている。・ ・ ・ これらのうち（それらが本当に切り離せればの話だが）第二および第三の意味で――つまり力を伴なわない非局所性という意味で――量子力学は非局所的理論だ。 ・ ・ ・ 　・ ・ ・ EPR の真髄は、量子力学が非局所的か不完全かのどちらかであることを素朴さ抜きに示していることにある。憶えば、アインシュタインは、局所性をまっとうな物理理論に欠かせない特性と考えており、それ故に量子力学の不完全性を主張した訳だ。もし不完全ならば、量子力学は微視的物理状態のもっと深い「隠れた変数」記述で補完されることにきっとなるだろうし、また、量子力学的状態はそうした深い状態を均したものに過ぎないことが明らかになるはずだと一般に期待されるに違いない。
　EPR 以降、量子力学の哲学への最も重要な貢献―― J. S. ベルの、その名を冠されている不等式に関する仕事――は、EPR の、正確には EPR-B の思考実験の深化と一般化から成る。

　ここで「EPR-B」と呼ばれているのは、アインシュタインとポドロフスキーとローゼンが量子力学の不完全性を主張するために考案した思考実験を、ボームが概念的に扱いやすい形に定式化しなおしたもののことで、簡単に云えば、次のようになる。
　ふたつのスピン 1/2 の原子からなる分子で、スピンの和が 0 になっているものを考える。この分子が、スピンの値が変わらないような仕方で分解し、その後ふたつの原子は互いに遠ざかって行くものとする。そこで、それらの間の距離が十分に大きくなってから一方の原子について任意の方向 d のスピン成分を測定して、例えば上向きという結果が得られたとすれば、スピンの和は依然として 0 な訳だから、もう一方の原子の d スピンは下向きであることが判ることになる。
　ふたつのスピン 1/2 の系 I と II からなる結合系 I + II のスピン状態は、テンソル積ヒルベルト空間 C² C² のヴェクトルによって表わせる。特に、このケースのような状態はシングレットと呼ばれるが、それを表わす単位ヴェクトル |singlet> は、

|singlet> = (1/2)|z, +>|z, -> - (1/2)|z, ->|z, +>

として定義できて、どんな方向 d についても次が成り立つ。

|singlet> = (1/2)|d, +>|d, -> - (1/2)|d, ->|d, +>

一方、部分系 I と II それぞれの d 方向のスピン成分を表わす C² C² 上の自己随伴作用素は S_d I および I S_d であり、これらのスペクトル分解は次のようになる。

S_d I = (/2)(|d, +><d, +| I ) - (/2)(|d, -><d, -| I )
I S_d = (/2)(I |d, +><d, +|) - (/2)(I |d, -><d, -|)

シングレット状態にある I + II の部分系としての I について d スピンを測定した結果が上向きとでる確率は

	<singlet|(|d, +><d, +| I )|singlet>
=	<singlet|(|d, +><d, +| I )((1/2)|d, +>|d, -> - (1/2)|d, ->|d, +>)
=	(1/2)<singlet|(|d, +>|d, -> - 0)
=	(1/2)(1/2)(<d, +|<d, -| - <d, -|<d, +|)(|d, +>|d, ->)
=	(1/2)(1 - 0) = 1/2

となり、II について d スピンを測定した結果が下向きとでる確率は

	<singlet|(I |d, -><d, -|)|singlet>
=	<singlet|(I |d, -><d, -|)((1/2)|d, +>|d, -> - (1/2)|d, ->|d, +>)
=	(1/2)<singlet|(|d, +>|d, ->) = 1/2

となる。また、I の d スピンを測定した結果が上向きであることが判っているときに II の d スピンを測定した結果が下向きとでる確率――いわゆる条件つき確率――は

	<singlet|(|d, +><d, +| |d, -><d, -|)|singlet>/<singlet|(|d, +><d, +| I )|singlet>
=	<singlet|(|d, +><d, +| |d, -><d, -|)((1/2)|d, +>|d, -> - (1/2)|d, ->|d, +>)/(1/2)
=	(1/2)<singlet|(|d, +>|d, -> - 0)/(1/2)
=	(1/2)/(1/2) = 1

となる。なお、|singlet> は自己随伴作用素 S_d I + I S_d の固有値 0 に対応する固有ヴェクトルであり、これは I と II の d スピンをそれぞれに測定した結果の値の和が 0 となる確率が 1 であることを意味する。
　２１２から２１８ページ目にかけては次のようなくだりがある。

ベルはつぎのようなより一般的な問題を問うた。そのような系にかんするスピンの測定結果は、二つの測定を同一方向ではなく、なんらかの２方向において、つまり互いに対して任意の角度で行ったときには、いかに相関づけられるか？ そして、その結果が二組の隠れた変数によって支配され、変数の各組が対の各メンバーにそれぞれ適用されるならば、それらの粒子はいかに相関づけられねばならないか？ ・ ・ ・
　ベルの答えはこうである。決定論的な理論、つまり局所的な隠れた変数理論によって制御された粒子のスピンは、ベルの不等式 (Bell inequalities) と呼ばれる特定の数学的関係を満足するようなしかたで相関づけられねばならない。
　じつのところ、ベルの不等式族が存在する。ベルの不等式は思考実験の成果ではないが、現実の実験によって検証することができ、１９７０年代の大半の仕事は、量子力学がベルの不等式を破るかどうかを発見することに向けられた。・ ・ ・ われわれは、P. H. エバーハードによる非常にエレガントなベルの一不等式の導出からはじめる。それはつぎのようになる。
　・ ・ ・ われわれは I の測定について２方向を、II の測定について２方向を考察しなければならない。前者を a と a'、後者を b と b' としよう。・ ・ ・
　・ ・ ・ 方向 a、a' と b、b' の各組合せについて何度も測定を繰り返すことによって、ある方向における I のスピン測定と、それとは別の方向における II のスピン測定との相関を測定することができる。・ ・ ・ I のスピン測定の方向を a とし、II のスピン測定の方向を b としよう。・ ・ ・ こうした諸結果は、方向 a と b に依存して、正に相関しているかもしれないし、負に相関しているかもしれないし、あるいはまったく相関していないかもしれない。したがって、われわれはその相関の尺度、あるいは相関の欠如を定義する必要がある。
　・ ・ ・ 相関 C (a, b ) はつぎのように決定することができる。I と II のスピン測定を多数 (N ) 回行う。・ ・ ・ a_n が「a 」方向における I の n 回目の測定結果であり、b_n が方向「b 」において I と相関する系 II についての n 回目の測定結果であるとすれば、N は無限になるので、

C (a, b ) = (1/N )Σ_na_nb_n

・ ・ ・ 　その数学的問題はこうである。C (a, b )、C (a, b' )、C (a', b )、および C (a', b' ) に関係する不等式をみつけよ。その不等式はなんらかの局所的な隠れた変数によって満足されるものであって、量子力学によって満足されるのではない。・ ・ ・
　・ ・ ・ I のスピンを方向 a で測定したときに得られるであろう結果を a_n としよう。これは +1 か -1 のどちらかである。同様に、I のスピンを方向 a' で測定したときに得られるであろう結果を a_n' としよう。これもまた +1 か -1 のどちらかである。
　もちろん、系を擾乱することなくこれらのスピンの両方を測定することはできない。しかし、測定されないスピンの結果は確定的に +1 か -1 のどちらかである、ということが仮定される。これは、I と II が決定論的な理論、つまり隠れた変数理論によってそれぞれ制御されるとすれば、完全に正しい仮定である。
　今度は相関系 II について、同じような量 b_n と b_n' についても定義する。
　さて、奇異にみえる量、

g_n = a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n' 　　[*]

について考察してみよう。
　われわれは g_n を操作して、いま望む不等式を得る。g_n は、

g_n = a_n(b_n + b_n' ) + a_n' (b_n - b_n' )

と書き直すことができることに、まず注目しておこう。
　・ ・ ・ b_n と b_n' はおのおの +1 か -1 のどちらかであるので、・ ・ ・ (b_n + b_n' ) か (b_n - b_n' ) のどちらかはゼロである。・ ・ ・ そしてゼロにならない方は +2 か -2 になる。a_n は +1 か -1 のどちらかなので、g_n = +2 or -2 が帰結する。ゆえに、そしてついに、g_n の絶対値は 2 となる。
　われわれは、g_n ではなくて C ( . , . ) を含む a_n 式を得たいのである。したがって、[*] からつぎのように書き

(1/n )Σ_n g_n = (1/n )Σ_n(a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n' )

そして、両辺の絶対値をとれば、

|C (a, b ) + C (a, b' ) + C (a', b ) - C (a', b' )| ≦ 2 　　［ベル‐１］

が得られる。
　これはベルの不等式の一つである。量子力学はベルの不等式を破る。世界がその不等式を破ることが判明しているのである。・ ・ ・
・ ・ ・ 　・ ・ ・ 現在までに行われた実験は、形式的に似たような装置を用いて、原子が励起状態から崩壊するあいだに生じる偏光した光子の相関を扱っている。光子検出器と偏光子［偏光を採りだすための光学素子。たとえば方解石］は完全に有効ではないし、その効率の悪さが、量子的非局所性によって生ずるわずかな統計的偏差を検出困難にするので、実験を実施することは困難である。しかし、いくつかの量子的相関については、ベルの不等式は実験的に偽であることが示されたということで、いまのところ合意に達している。

　原文は次の通り。

Bell asks the more general question: how will the results of spin measurements on such a system be correlated when you make two measurements not in the same direction, but in any pair of directions, aｔ any angle with respect to one another that you like? Furthermore, how must they be correlated if the results are governed by two sets of hidden variables, each set applying separately to each member of the pair? . . . Bell's answer is that the spins of particles controlled by a deterministic, local hidden-variables theory, must be correlated in such a way as to satisfy certain mathematical relations called the Bell inequalities.
　 There is in fact a family of Bell inequalities. Bell inequalities, though they are the result of thought-experiments, can be tested by real experiments and much work in the 1970s was directed to finding out if quantum mechanics violated them. . . . We begin with a very elegant derivation due to P. H. Eberhard of one of the Bell inequalities, which is as follows.
　 . . . we have to consider two directions for the measurements on I, let these be a and a', and two directions for the measurements on II, let these b and b'. . . .
　 . . . by making a large number of measurements for each combination of directions a, a', b, b' one can measure the correlation between the spin measurements on I in a given direction and on II in another direction. . . . Let the direction of spin measurement on I be a and on II be b. . . . These results may be positively correlated, negatively correlated or not correlated at all, depending on the directions a and b. So we need to define a measure of their correlation, or lack of it.
　 . . . One can determine the correlation C (a, b ) as follows. Make a large number N of the spin measurements on I and II. . . . if a_n is the result of the nth measurement on I in the direction ‘a ’, and b_n is the corresponding nth measurement on the system II in the direction b, then, as N goes to infinity

C (a, b ) = (1/N )Σ_na_nb_n .

. . . 　 The mathematical problem is this: find an inequality relating C (a, b ), C (a, b' ), C (a', b ), andC (a', b' ) which is satisfied by any local hidden-variables theory but not by quantum mechaics. . . .
. . . 　 Let the result that whould be obtained if spin of I were measured in direction a be a_n . This will be +1 or -1. Similarly, let the result that whould be obtained if the spin of I were measured in direction a' be a_n'. This again will be +1 or -1.
　 Of course one cannot measure both these spins without disturbing the system. But one supposes that the result of the unmeasured spin is determinately either +1 or -1. This is a perfectly correct assumption given that I and II are controlled separately by a deterministic, hidden-variabes theory.
　 One now defines similar quantities b_n and b_n' for the correlated system II.
　 Now consider the odd-looking quantity

g_n = a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n'. 　　[*]

We manipulate g_n to obtain the desired quantity. But first note that one can rewrite g_n as

g_n = a_n(b_n + b_n' ) + a_n' (b_n - b_n' )

. . . 　 Since b_n and b_n' are either +1 or -1, . . . either

(b_n + b_n' )

or

(b_n - b_n' )

is zero. . . . The one which is not zero is either +2 or -2. Since a_n is either +1 or -1 it follows that g_n = +2 or -2.
　 Hence, and lastly, the absolute value of g_n , that is |g_n |, is 2.
　 We want to get an expression involving C ( , ) rather than g_n . So from [*] we can write

(1/N )Σ_n g_n = (1/N )Σ_n(a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n' )

and taking absolute value of both sides, we get

|C (a, b ) + C (a, b' ) + C (a', b ) - C (a', b' )| ≦ 2 　　(BELL-1)

　 This is one of Bell inequalities.
　 Quantum mechanics violates it. It turns out that the world violates it. . . . . . . 　 . . . The experiments performed to date use the formally similar set-up of polarized photon correlation generated during the decay of an atom from an excited state. The experiments are difficult to perform because photon detectors and polarizers are not perfectly efficient, and their inefficiency makes the small statistical deviations due to quantum nonlocality difficult to detect. But the current consensus is that the Bell inequalities have been shown to be false experimentally for some quantum correlations. (pp.118-122)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

ベルは、次のような、より一般的な問題を考えた。そうした［シングレット状態にある］系に対するスピン測定の結果の相関は、ふたつの測定を、同一方向ではなく、任意の角度をなすふたつの方向についておこなった場合、どうなるだろうか？ さらに、もしそれらの結果が、粒子対のそれぞれの粒子に別々に関わる二揃いの隠れた変数によって決まるとすれば、相関はどうなっていなければならないか？ ・ ・ ・ ベルの答は、決定論的な局所的隠れた変数理論によって制御される粒子のスピンはベルの不等式と呼ばれる或る数学的関係を充たすように相関していなければならない、というものだ。
　実際には、ベルの不等式の族が存在する。ベルの不等式は思考実験の成果だが、現実の実験によってテストすることができて、１９７０年代には多くの仕事が、それらが破れるかどうかを調べるのにあてられた。・ ・ ・ 我々は、ベルの不等式のひとつの P. H. エバーハードに由る非常にエレガントな導出からはじめよう。それは次の通り。
　・ ・ ・ I に対する測定に関してふたつの方向を考える必要がある。それらを a と a' としよう。また、II についても同様であり、それらを b と b' とする。・ ・ ・
　・ ・ ・ 方向 a、a'、b、b' の組み合わせのそれぞれについて多数回測定を繰り返すことによって、I に対するひとつの方向についてのスピン測定と II に対する別の方向についてのスピン測定の間の相関を計ることができる。・ ・ ・ I に対するスピン測定の方向を a とし、II に対する方向を b としよう。・ ・ ・ これらの［測定］結果は、方向 a と b 次第で正に相関していたり負に相関していたりするかもしれないし、全く相関していないかもしれない。そこで、それらの相関の、というより相関の不足についての尺度を定義する必要がある。
　・ ・ ・ 相関 C (a, b ) は次のように規定できる。N を大きな数として、I と II についてスピン測定を N 回おこなう。・ ・ ・ a_n を I に対する a 方向についての n 回目の測定結果［の /2 を単位とした値］、b_n を II に対する b 方向についての n 回目の測定結果として、

C (a, b ) = lim_{N →∞}(1/N )Σ _{1≦n ≦N} a_nb_n

・ ・ ・ 　問題は数学的にこうなる。C (a, b )、C (a, b' )、C (a', b )、C (a', b' ) に関わる不等式で、どんな局所的隠れた変数理論によっても充たされるが量子力学によっては充たされないものを探せ。・ ・ ・
・ ・ ・ 　I のスピンを a 方向について測定したならば得られるであろう結果を a_n としよう。これは +1 か -1 のはずだ。同様に、I のスピンを a' 方向について測定したならば得られるであろう結果を a_n' としよう。これもまた +1 か -1 のはずだ。
　もちろん、系を攪乱することなく両方のスピンを共に測定することはできない。しかし、実行されなかったスピン測定の［いわゆる反事実的］結果は［ II に対する測定とは独立に］ +1 か -1 のどちらかに定まっているものとする。この仮定は、I と II が決定論的な［局所的］隠れた変数理論によって別々に制御されるとすれば、全く正当だ。
　系 II についても量 b_n と b_n' を同様に定義する。
　そこで、一見奇妙な量

g_n = a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n' 　　[*]

を考える。
　我々は求める不等式を得るために g_n を操作するのだが、まず、g_n は、

g_n = a_n(b_n + b_n' ) + a_n' (b_n - b_n' )

と書きなおせることに注意しよう。
・ ・ ・ 　b_n と b_n' は +1 か -1 のどちらかだから、・ ・ ・

(b_n + b_n' )

か

(b_n - b_n' )

のどちらかは 0 だ。・ ・ ・ 0 でない方は +2 か -2 だ。a_n は +1 か -1 のどちらかだから、g_n = +2 または g_n = -2 ということが帰結する。
　よって、結局、g_n の絶対値つまり |g_n | は 2 だ。
　我々が欲しいのは、g_n ではなく C ( , ) を含む表現だ。ところが、[*] から

(1/N )Σ _{1≦n ≦N} g_n = (1/N )Σ _{1≦n ≦N} (a_nb_n + a_nb_n' + a_n'b_n - a_n'b_n' )

と書けるので、両辺の絶対値をとって［ N → ∞ とすれば］、次が得られる。

|C (a, b ) + C (a, b' ) + C (a', b ) - C (a', b' )| ≦ 2 　　[BELL-1]

　これはベルの不等式のひとつだ。量子力学はこれを破る。世界がこれを破ることも判っている。・ ・ ・
・ ・ ・ 　・ ・ ・ これまでに行われた［主な］実験は、或る種の原子が励起状態から遷移するあいだに生じる光子の偏極の相関という［スピンの場合と］形式的に同様のからくりを利用している。光子検出器や偏極器の効率は完全とはいかない訳で、それらの効率の低さが量子的非局所性に由来する小さな統計的偏差の検出を困難にするため、そうした実験を遂行するのは難しい。しかし、いくつかの量子的相関に関しては、ベルの不等式は正しくないことが実験的に示されたというのが現在のコンセンサスだ。

　量子力学が [BELL-1] を破る理論的帰結をもつことは、次のようにして示せる。
　まず、直交座標系 Oxyz を、z 方向が a に一致し xz 平面が b を含むようにとることにして、θ を a と b がなす角度とすれば、シングレット状態にある I + II の部分系としての I の a スピン（つまり z スピン）と II の b スピンを共に測定した結果が両方上向きとでる確率および両方下向きとでる確率は、量子力学によれば、それぞれ

	<singlet|(|z, +><z, +| |b, +><b, +|)|singlet>
=	<singlet|(|z, +><z, +| |b, +><b, +|)((1/2)|z, +>|z, -> - (1/2)|z, ->|z, +>)
=	(1/2)<singlet|(<b, +|z, ->|z, +>|b, +> - 0)
=	(1/2)(1/2)<b, +|z, ->(<z, +|<z, -| - <z, -|<z, +|)(|z, +>|b, +>)
=	(1/2)<b, +|z, -><z, -|b, +>
=	(1/2)sin(θ/2)exp(-i 0/2)sin(θ/2)exp(i 0/2)
=	(1/2)sin2(θ/2)

	<singlet|(|z, -><z, -| |b, -><b, -|)|singlet>
=	<singlet|(|z, -><z, -| |b, -><b, -|)((1/2)|z, +>|z, -> - (1/2)|z, ->|z, +>)
=	(1/2)<singlet|(<b, -|z, +>|z, ->|b, ->)
=	(1/2)(1/2)<b, -|z, +>(<z, +|<z, -| - <z, -|<z, +|)(|z, ->|b, ->)
=	(1/2)<b, -|z, +><z, +|b, -> = (1/2)sin2(θ/2)

となり、一方が上向きで他方が下向きとでる確率は、それぞれ

	<singlet|(|z, +><z, +| |b, -><b, -|)|singlet>
=	<singlet|(|z, +><z, +| |b, -><b, -|)((1/2)|z, +>|z, -> - (1/2)|z, ->|z, +>)
=	(1/2)<singlet|(<b, -|z, ->|z, +>|b, ->)
=	(1/2)(1/2)<b, -|z, ->(<z, +|<z, -| - <z, -|<z, +|)(|z, +>|b, ->)
=	(1/2)<b, -|z, -><z, -|b, -> = (1/2)cos2(θ/2)

	<singlet|(|z, -><z, -| |b, +><b, +|)|singlet>
=	<singlet|(|z, -><z, -| |b, +><b, +|)((1/2)|z, +>|z, -> - (1/2)|z, ->|z, +>)
=	(1/2)<singlet|(-<b, +|z, +>|z, ->|b, +>)
=	(1/2)(1/2)<b, +|z, +>(<z, +|<z, -| - <z, -|<z, +|)(-|z, ->|b, +>)
=	(1/2)<b, +|z, +><z, +|b, +> = (1/2)cos2(θ/2)

となる。よって、ふたつの結果の（/2 を単位とした）値の積が +1 となる確率および -1 となる確率は、それぞれ

(1/2)sin²(θ/2) + (1/2)sin²(θ/2) = sin²(θ/2)
(1/2)cos²(θ/2) + (1/2)cos²(θ/2) = cos²(θ/2)

となるから、相関は、理論的には、

C (a, b ) = sin²(θ/2) - cos²(θ/2) = -cos(θ )

となる。そこで、今度は、a と b を同一方向とし、a' と b' を、a と同一平面上にあって a に対してそれぞれπ/4 および -π/4 の角度をなす方向とすれば、C ( , ) は座標系のとり方には依存しないから、

C (a, b ) = -cos(0) = -1,　　C (a, b' ) = -cos(-π/4) = -1/2
C (a', b ) = -cos(π/4) = -1/2,　　C (a', b' ) = -cos(π/2) = 0

となるが、これを [BELL-1] の左辺に当てはめると、

	|C (a, b ) + C (a, b' ) + C (a', b ) - C (a', b' )|
=	|(-1) + (-1/2) + (-1/2) - 0|
=	1 + 2

となる。（もちろん 1 + 2 は 2 より大きい訳で、これは [BELL-1] と矛盾する。）
　[BELL-1] が理論的に成り立たないということは、量子力学を局所的隠れた変数理論で補完するのが不可能なことを示している。２１９から２２１ページ目には次のようなくだりがある。

　隠れた変数が背後にあるという理論と量子力学が整合しないということの証明は、ベルの仕事に３０年以上さかのぼる。フォン・ノイマンは１９３２年に、量子系のどんな状態もすべてのオブザーバブルに対する確定値を同時にもつことはできないことを示した。かれの議論は一組みの仮定を使用しており、少なくともその一つはかなり問題を含んでいる。にもかかわらず、かれの名声と、かれの証明の経験的な意味が曖昧であること、そして隠れた変数の可能性を否定する便利な哲学が含まれていたという事実とは、すべてがあいまってアンチ隠れた変数の立場をとる正統派をつくりあげた。・ ・ ・
　フォン・ノイマンはつぎのように仮定した。1 よりも大きい次元をもつヒルベルト空間に作用するすべてのエルミート演算子はオブザーバブルを表すこと。特殊な空のオブザーバブル 1 ――単位元――について、その期待値 <1> = 1 であること。各オブザーバブル A と各実数 r について、r<rA > = r<A > であること。もし A が一つのオブザーバブルで、その値がつねにゼロより大きいかゼロに等しいならば、A の期待値もまたゼロより大きいこと。
　これらの諸仮定はまったく無害なのだが、フォン・ノイマンは５番目の仮定をした。かれは、その仮定は隠れた変数の強い形式にもあてはまるとしたのであるが、すなわちこうである。任意のオペレーター A, B, C . . . について、<A + B + C + . . . > = <A > + <B > + <C > + . . . であること。これによってかれは、

<X ²> ≠ [<X >]²

であるようなオブザーバブル X が存在することを証明できるようになっている。言い換えれば、どんな量子状態についても、分散をまぬがれないオブザーバブルが存在する、つまり値を確定できないオブザーバブルが存在するのである。
　・ ・ ・ もしこの仮定がつぎのような形式にも本当に適用するならば、隠れた変数不在定理を導くことは非常にたやすい。すなわち、h を隠れた変数（つまり、この場合では一つのベクトルと考えるべき諸変数）とするならば、両立しない A と B についてさえ、

(A + B )(h ) = A(h ) + B(h ) 　　[**]

が成立する。この等式が述べているのは、A + B の値は、A と B を別々に決定する隠れた変数の値によって確定されるだろう、ということである。ゆえに、隠れた変数は存在しない。 ・ ・ ・ 　さて、証明にはいろう。これはルドルフ・パイエルスによるものである。x 軸に対して θ 方向にスピン 1/2 をもつ粒子を考えると、そのスピン成分 s' は、

s' = s_x cosθ + s_y sinθ 　　[***]

となる。量子力学によれば、s'、s_x 、および s_y は、それぞれ +1/2 か -1/2 の値しかとれない。隠れた変数理論がこの結果を再現するためには、われわれはつねに値 +1/2 か -1/2 をとる関数 s_x(h ) と s_y(h ) とを発見しなければならないが、したがって [***] によって与えられる s'(h ) の値もまた +1/2 か -1/2 であり、それは（θ が π/4 の倍数のとき以外は）不可能である。

　原文は次の通り。

A demonstration that quantum mechanics is inconsistent with an underlying hiden-variable theory predates Bell's work by more than thirty years. In 1932 von Neumann showed that no state of a quantum system can assign simultaneously definite values to all the quantum-mechanical observables. The arguments put forward by von Neumann employed a set of assumptions at least one of which was highly questionable. Nevertheless, his prestige, the obscurity of the emprical significance of his proof, and the fact that there was a handy philosophy which denied the possibility of hidden-variables theories all conspired to generate an anti-hidden-variables orthodoxy. . . .
　 In his proof von Neumann assumed that every Hermitian operator on a Hilbert space of dimension greater than one represents an observable, that for a particular vacuous observable 1 ―― the identity ―― the expectation value

<1> = 1,

that for each observable A and each real number r

<rA> = r<A>,

that if A is an observable whose value is always greater than or equal to zero then the expectation value of A should also be greater than zero.
　 These assumptions are innocent enough but von Neumann assumed a fifth, which he assumed to hold also in strong form for the hidden variables, namely that for arbitrary observables A, B, C . . .

<A + B + C + . . . > = <A> + <B> + <C> + . . .

This enables him to prove that there is always an observable X such that

<X²> ≠ [<X>]².

In other words for any quantum state there is an observable which is not dispersion-free, an observable which, in other words, is not definite in value.
　 . . . If it does hold in the following form, namely that if h is the hidden variable (or variables, in which case think of h as a vector), then even for incompatible A and B

(A + B)(h) = A(h) + B(h) 　　[**]

an equation which says that the value A + B will be determined by the values of the hidden-variables which determine A and B separately, then it is very easy to derive a no hidden-variable theorem. . . . 　 Now for the proof, which is due to Rudolf Peierls.
　 Consider the spin component of s' of a spin-1/2 particle, in a direction in the x-y plane at an angle θ to the x-axis,

s' = s_x cosθ + s_y sinθ 　　[***]

According to quantum mechanics s', s_x , and s_y each take only the values +1/2 or -1/2. For a hidden-variables theory to reproduce this result we must find functions S_x(h) and S_y(h) which always take the values +1/2 or -1/2 such that the value of S '(h) given by [***] is also +1/2 or -1/2, which is impossible (except when θ is a multiple of π/4). (pp.122-124)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　量子力学は隠れた変数理論と整合的でないとする論証のひとつは、ベルの仕事に三十年あまり先立つ。フォン・ノイマンは、１９３２年に、凡ての量子力学的オブザーヴァブルに一斉に明確な値を割り振るような状態は在り得ないことを示した。その論法には一組の仮定が用いられており、少なくともそのうちのひとつは大いに疑わしいものだったが、しかし、彼の名声と、その証明の経験的意義の不明さ、そして隠れた変数理論の可能性を否定する手頃な哲学が在ったという事実が相俟って、隠れた変数嫌いの正統派を生み出した。・ ・ ・
　その証明において、フォン・ノイマンは、次元が 1 より大きいヒルベルト空間上のどのエルミート作用素［つまり自己随伴作用素］も何らかのオブザーヴァブルを表わすこと、および、特別の空虚なオブザーヴァブル 1 ――値が恒等的に 1 のオブザーヴァブル――について、その期待値は

<1> = 1

となること、それぞれのオブザーヴァブル A およびそれぞれの実数 r について

<rA> = r<A>

となること、A をその値が恒に 0 以上であるようなオブザーヴァブルとすれば、A の期待値もまた 0 以上であることを仮定した。
　これらの仮定は全く無害だが、フォン・ノイマンは次のような第五の仮定をおいた。任意のオブザーヴァブル A, B, C, . . . について

<A + B + C + . . . > = <A> + <B> + <C> + . . .

彼は、さらに、これが隠れた変数に対して強い形で成り立つことを仮定したのだが、ともあれ、この第五の仮定によって、

<X²> ≠ <X>²

となるようなオブザーヴァブル X が恒に存在すること、云い換えれば、どんな量子状態についても、それに応じて、ばらつきを免れない、値がはっきりしない何らかのオブザーヴァブルが存在することが証明できる。
　・ ・ ・ その仮定が次のような形で本当に成り立つとすれば、つまり、h を隠れた変数（あるいは変数の組）として、両立不能な A と B についても

(A + B)(h) = A(h) + B(h) 　　[**]

ということが成り立つとすれば、この等式は A + B の値がA と B ［の値］を別々に決定する隠れた変数の値によって定まることを意味する訳だが、すると、ある種の隠れた変数の存在不能定理を導き出すことは非常にたやすい。 ・ ・ ・ 　そこで証明だが、以下はルドルフ・パイエルスに由る。
　スピン 1/2 の粒子の、x-z 平面上にあって z 軸に対して角度 θ をなす方向のスピン成分

S ' = S_z cosθ + S_x sinθ 　　[***]

を考える。量子力学によれば、S '、S_z 、S_x は何れも［ を単位として］+1/2 か -1/2 の値しかとらない。隠れた変数理論がこの結果を再現するには、恒に +1/2 か -1/2 の値をとる関数 S_z(h) と S_x(h) で、[***] によって規定される S '(h) の値をもまた +1/2 か -1/2 にするようなものをみつける必要があるが、それは（θ が π/2 の整数倍の場合を除いて）不可能だ。

　フォン・ノイマンは、『量子力学の数学的基礎』の第四章で、オブザーヴァブルとその期待値に関するいくつかの一般的な仮定から、或る意味において、ばらつきのないアンサンブルは存在しないことを導いている。その筋書を簡単に再構成してみれば、次の通り。
　まず、系 S に結びつけられるヒルベルト空間 H 上のそれぞれの自己随伴作用素には S のオブザーヴァブルがひとつづつ対応しているものと仮定して、O_S,H をそのようなオブザーヴァブル全体の集合とする。そして、次を充たすような O_S,H から実数全体の集合 R への写像 E_S,H を考える。

• 恒等作用素 I に対応するオブザーヴァブル 1 について E_S,H(1) = 1。
• O_S,H に属すどんなオブザーヴァブル A およびどんな実数 λ についても E_S,H(λA) = λE_S,H(A)。（ただし、「λA」はオブザーヴァブル A のとる値を λ 倍することによって得られるオブザーヴァブルを表わす。）
• O_S,H に属すどんなオブザーヴァブル A についても、A が恒に 0 以上の値をとるならば E_S,H(A) ≧ 0 。
• A、B、C が H 上の自己随伴作用素で C = A + B ならば、それらに対応するオブザーヴァブル A、B、C について、E_S,H(C) = E_S,H(A) + E_S,H(B)。

H が有限次元の場合、E を密度作用素 D によって表わされるアンサンブルに関するオブザーヴァブル A にその期待値 trace(DA ) を対応づける写像とすれば、E はこれらを充たす。（実際、この四つの条件は、通常の確率論における期待値の一般的属性に沿ったものになっている。なお、フォン・ノイマンのこの仕事は、コルモゴロフによって数学としての確率論の近代化にけりがつけられる前のものらしいが、大事なのは確率の解釈の方だろう。フォン・ノイマンが拠っていたのは、当時フォン・ミーゼスによって補強されたばかりの相対頻度解釈だったようだ。）そこで、これらの条件を充たすような写像 E_S,H を S に関する期待値汎関数と呼ぶことにして、それぞれの期待値汎関数 E_S,H には S を要素としてもつアンサンブル e がひとつづつ対応しているものと仮定する。（H が無限次元の場合、期待値汎関数をもたないアンサンブルも在るが、その点は以下の話には関わりが無い。）
　そうすると、どんな期待値汎関数 E_S,H についても密度作用素 D がひとつだけ在って、O_S,H に属すどんなオブザーヴァブル A についても、A を A に対応する自己随伴作用素、{v_i }_i を A の定義域に含まれるような H の正規直交基底とすれば、

E_S,H(A) = Σ_i <v_i , DAv_i >

となることが示せる。（自己随伴作用素 A の定義域は稠密だから H の正規直交基底を必ず含む。）よって、E_S,H に対応するアンサンブル e は E_S,H に対応する密度作用素 D によって表わせることになる。
　次に、期待値汎関数 E_S,H に対応するアンサンブルに関するオブザーヴァブル A の分散 V(A) を、通常の確率論に倣って、

V(A) = E_S,H((A - E_S,H(A))²)

として定義し、さらに、S を要素としてもつアンサンブル e がばらつきなしであるとは、e が期待値汎関数をもち、O_S,H に属すどんなオブザーヴァブル A についても

V(A) = 0

となることだと定める。すると、これらの定義から、e がばらつきなしならば、E_S,H を e に対応する期待値汎関数として、O_S,H に属すどんな A についても

E_S,H(A²) = (E_S,H(A))²

となることが帰結する。（ただし、「A²」は A のとる値を二乗することによって得られるオブザーヴァブルを表わす。このオブザーヴァブルに対応する自己随伴作用素は、A に対応する作用素 A の冪 A²（= AA ）だ。）
　そこで、もし、S を要素としてもつばらつきなしのアンサンブルが在るとすれば、それを表わす密度作用素 D が在って、H 上のどんな自己随伴作用素 A についても、{v_i }_i を A² の定義域に含まれるような H の正規直交基底として、

Σ_i <v_i , DA²v_i > = (Σ_i <v_i , DAv_i >)²

となるのでなければならないが、しかし、その一方、この条件をみたすような作用素 D は（H の次元が 1 というトリヴィアルなケースを別にすれば）密度作用素ではあり得ないことが示せるので、矛盾をきたす。よって、ばらつきなしのアンサンブルは存在しない。
　ただし、この証明は、量子力学の枠組の中には、オブザーヴァブルおよび期待値汎関数に関する上の仮定のもとでは、上の意味でのばらつきなしのアンサンブルの入る隙は無いことを示しているに過ぎない。しかも、期待値汎関数のステータスはどうも疑わしい。ちなみに、１９５７年に発表されたグリーソンの定理は、そんな胡散臭い期待値汎関数の替わりに、ヒルベルト空間 H の部分空間全体のなす束 L(H) 上の確率測度という見通しのいい道具立てを用いることによって、上の結果をきちんと証明しなおしたものだとも云えるだろう。
　ところで、ギビンズの云う強い形の仮定とは、隠れた変数が充たすべき条件のことであり、次のように云い換え得る。

• A、B、C が H 上の自己随伴作用素で C = A + B ならば、A、B、C をそれらに対応するオブザーヴァブル、A(h)、B(h)、C(h) を隠れた変数 h によって定まる A、B、C の値として、C(h) = A(h) + B(h)。

しかし、このようなことをフォン・ノイマンがストレートに要請していた訳ではない。（結局はそれと大差ないにしても。）隠れた変数に関して、彼はいかにも舌足らずな云い方をしているが、それを補ってみれば、次のようになるだろう。
　隠れた変数によって凡てのオブザーヴァブルに値を割り振るような状態が定まるとすれば、そうした状態に対応するアンサンブルの期待値汎関数は、それぞれのオブザーヴァブルに件の状態によって割り振られる値を対応づける写像であるほかないが、そのような写像は期待値汎関数に対する第四の条件を充たし得ない。したがって、隠れた変数は在り得ない。
　この推論は、しかし、量子力学に依拠して導入した E_S,H 汎関数と通常の確率論の意味での期待値汎関数（つまり確率変数にその期待値を対応づける写像）を一緒くたにしてしまっている。フォン・ノイマンは、隠れた変数は量子力学によっては規定し尽くされていない状態を完全に特定するものだと仮定していたが、そうした状態に対応するアンサンブルにまで E_S,H 汎関数という概念が通用するとする根拠は無い。その点については、ライヘンバッハが夙に云っている。フォン・ノイマンの証明は、量子力学の法則はあらゆる類のアンサンブルについて妥当だという仮定に基づいているが、量子力学の非決定論が批判される場合には、この仮定もまた問題視されるだろう、と。（ギビンズの云う「手頃な哲学」とは、いわゆる意味の検証理論を柱とする論理実証主義のことだと思われるが、ライヘンバッハはその傍流に位置する科学哲学者だった。正統派の擡頭は、科学史家クーンを真似て云えば、量子力学が当時既に、ボーアの、というよりはハイゼンベルク流のコペンハーゲン解釈のもとで、通常科学化していたことを示すに過ぎないのではなかろうか。）
　なお、グリーソンの定理から、次元が 2 より大きい可分なヒルベルト空間 H の部分空間全体のなす束 L(H) 上の確率測度で { 0, 1 } を値域とするようなもの――いわゆる二値測度――は存在しないことが帰結する。これは、フォン・ノイマンが狙いを定めていたような隠れた変数は、やはり在り得ないことを意味する。

２００４年春（２００５年４月増補改訂）　　大熊康彦

---

雑録　／　『量子論理の限界』について ( I ) ( II ) ( III ) ( IV ) ( V )