雑録

---

『量子論理の限界』について ( I )

　何の因果か、俺は量子力学の「観測問題」というやつに興味をもってしまって、その手の本をぼちぼち読んだりしているのだが、それでひどい翻訳本にぶつかった。金子務と宇多村俊介共訳の『量子論理の限界』（産業図書）だ。
　拙い行文を我慢して読んでも、この本には何のことやらよく判らないところがあちこちに在って、これは翻訳が悪いに違いないと思ってはいたのだが、その後ギビンズ (Peter Gibbins) の原著 Particles and Paradoxes (Cambridge University Press, 1987) が手に入ったので、照らし合わせてみると、それが予想以上にひどいのだった。
　以下に殊に問題のある箇所を拾ってお目にかけよう。ついでに量子力学の哲学へのちょっとした案内を決め込むことにする。（なお、訳者らが底本にしたのは第二版のための原稿だそうだが、俺が手に入れたのは第一版だ。おそらく第二版は陽の目を見ていないのではないかと思うが、ともあれ、その点は考慮に入れつつ見ていくつもりだ。）

1. 形而上学（あるいは超‐物理学）　(Meta-physics)
2. 自然哲学者のための量子力学 ( I )　(Quantum mechanics for natural philosophers ( I ))
3. 波動‐粒子の２重性　(Wave-particle duality)
4. コペンハーゲン解釈 ( I )　(The Copenhagen interpretation ( I ))
5. コペンハーゲン解釈 ( II )　(The Copenhagen interpretation ( II ))
6. 自然哲学者のための量子力学 ( II )　(Quantum mechanics for natural philosophers ( II ))
7. 射影公準　(Projection postulates)
8. 非局所性と隠れた変数　(Nonlocality and hidden variables)
9. 使い勝手の量子論理　(A user-friendly quantum logic)
10. 量子論理　(Quantum logic: what it can and can't do)

*

　まず、１ページ目には次のようなくだりがある。

物理理論はまた、科学的実験によって経験世界に照らして検証され、さらに絶え間なく技術装置や兵器に応用されてゆく。われわれはこの事実を十分深刻に受けとめねばならない。だがいったいなぜ、もっと厳密にいえばいかなる点で、われわれがそれほど深刻に受けとめるべきそのことが科学の哲学の問題となるのか。しかしわれわれはこれを問題としなければならないし、もし世界の在り方をもっともうまく説明するものはなにかと尋ねられるとしたら、われわれの大半は物理学の基本理論を引き合いにだすであろう。

　これに対応する原文は次の通り。

They [the theories of physics] are also tested against the world in experiment and are continuously applied in technological devices and in weaponry. We take them seriously. Just why, and in precisely what respects, we should take them seriously is a problem for the philosophy of science. But we do, and if we were asked what is our best account of the way the world is, most of us would cite the fundamental theories of physics. (p.1)

　これは次のような意味だろう。

物理理論はまた、実験によって世界に照らして検証され、技術装置や兵器に絶え間なく応用されている。我々は物理理論をまじめに受けとっている。いったい何故、そして厳密にはどんな点で、まじめに受けとるべきなのかは、科学哲学の問題だが、とにかく我々はそう受けとっているし、世界の在り方に関する最良の説明は何かと訊かれれば、たいていのひとは物理学の基本理論を引き合いに出すだろう。

　この第一章は、「荘重体の形而上学」つまり「無と肱掛椅子から究極の実在に関する新たな概念を捏ね上げる天才哲学者の産物」は、ここ百年ぐらいの間に廃れてしまった、という話ではじまっている。それは、その成果が往々にして馬鹿気ていたせいばかりではない、と著者ギビンズは云う。ここでは、そんな形而上学に物理理論が対比されている訳だ。

　２ページ目には次のようなくだりがある。

核兵器やトランジスタ、あるいは現在われわれのコミュニケーション・システムをつくっているマイクロチップなどを通して、じつにわれわれの技術文化が全体として、究極の量子力学のテクノロジーによって基礎づけられてきている（またそのことが脅威になってきている）。しかしながら、われわれの科学文化と技術文化において量子力学がきわめて重要であるにしても、そのことだけでは量子力学の哲学が生まれるには十分ではない。
　また量子力学は、物理学の基本理論としても十分なものではない（蛇足ながら、その非相対論的な形式にかんしては確かにそうである）。

　これは一見まともだが、実はそうでない。原文は次の通り。

　 One must of course admit that through nuclear weaponry, the transistor, and now the microchip, our system of communication, indeed our technoculture as a whole, has come to be based on and threatened by ultimately quantum-mechanical technology. But the importance of quantum mechanics in our scientific and technical culture is not sufficient to generate a philosophy of quantum mechanics.
　 Nor is it sufficient that quantum mechanics is a fundamental theory of physics which, incidentally, in its nonrelativistic form it certainly isn't. (p.1f.)

　これは次のような意味だろう。

　核兵器やトランジスタや、近頃ではマイクロチップを通じて、我々のコミュニケーションのシステムが、それどころか技術文化全体が、つまるところ量子力学的なテクノロジーに基づくようになり、それによって脅かされるに至っていることは、もちろん認めざるを得ない。しかし、我々の科学や技術の文化における量子力学の重要性は、量子力学の哲学を生むに足るものではない。
　また、量子力学が物理学の基本理論であることも、それに足るものではない。ちなみに、量子力学は、非相対論的な形においては、基本理論ではない。

　３ページ目には次のようなくだりがある。

　量子力学の哲学が存在するからといって、その事実が量子力学の正しさの問題と関わるわけでもない。量子力学は「正しいとみなされる」が、哲学的関心の薄い他の物理理論は「誤りとみなされる」、ということはできない。量子力学が正しいとは理解されてはいない。

　原文は次の通り。

　 The fact that there is a philosophy of quantum mechanics does not imply the truth of quantum mechanics. One cannot say that the quantum theories are known to be true, whereas other less philosophically interesting theories are known to be false. Quantum mechanics is not known to be true. (p.2)

　これは次のような意味だろう。

　量子力学の哲学が存在するという事実は、量子力学の正しさを伴いはしない。量子論は正しいことが判っているのに対して、哲学的にさほど興味のない他の物理理論は間違っていることが判っている、とは云えない。量子力学が正しいと判っている訳ではない。

　量子力学の哲学が重要なのは、量子力学が古典論的世界像を覆してしまったからだ、とギビンズは云う。そこで、話はその古典論的世界像に移る。
　８から９ページ目にかけては次のようなくだりがある。

　エーテル仮説をとると、光の速度はエーテルに対応した速度であることになる。それゆえに、つねに光の速度への関係を含むマクスウェル方程式は、ニュートンの運動の諸法則がもつ普遍性に欠けざるをえない。なぜならマクスウェル方程式は、加速のないあらゆる準拠枠では正しいままであるが、エーテルにかんして静止準拠枠では正しくなくなるからである。場と粒子の２元論はそれ自身未解決のままであった。

　原文は次の通り。

　 Given the aether hypothesis, the speed of light is its speed relative to the aether. Therefore Maxwell's equations, which contain a constant referring to the speed of light, must lack the universality of Newton's laws of motion, for these were held to be true in all unaccelerated frames of reference and not just those at rest with respect to aether. The dualism of field and particle was unsettling in itself. (p.5)

　これは次のような意味だろう。

　エーテル仮説をとれば、光速は、エーテルに対する光の速さだ。よって、光速を示す定数を含むマックスウェル方程式は、ニュートンの運動法則がもつような普遍性を欠かざるを得ない。ニュートンの法則は、エーテルに対して静止した座標系だけでなく、すべての加速されていない座標系において正しいと考えられていたのだから。場と粒子の二元論は本質的に不安定だった。

　１０ページ目には次のようなくだりがある。

　特殊相対性理論において、時空は時間と空間という別々の存在から受け継がれている。一般相対性理論においては、時空は歪められ、このことは重力という力としてわれわれにどのようにみえるか、という問題を生んだ。

　原文は次の通り。

　 In special relativity space-time takes over from space and time is perhaps the aether but in a new guise. In general relativity space-time is warped and this generates what appears to us the force of gravity. (p.6)

　これの前半はどうも要領を得ないが、ギビンズが云いたかったのは、たぶん次のようなことだろう。

　特殊相対性理論においては、時空連続体は、空間と時間を引き継ぐもので、おそらくは、新たに装われたエーテルだ。一般相対性理論においては、時空連続体は歪められ、それが、我々には重力とみえるものを生む。

　相対性理論は、その哲学的インパクトは強かったものの、実在の確定性を温存していてネオクラシカルだとギビンズは云う。そこで話は量子論に移り、さらに物理学の哲学の意義に及ぶ。それに関連する註の中に次のようなくだりがある。

ナンシー・カートライトもイーアン・ハッキングも、別の著作では、最近の物理学の哲学において支配的ないくつかの趨勢に対して異なった意見を述べている。
　イーアン・ハッキングの『表現と介入』は、理論を犠牲にしてわれわれの物理学のイメージにおける実験の役割を格上げしようと試みており、また、存在論を介在させる源泉として、ハッキングのいう表現の活動主義理論 (activist theory of representing) を説明することに乗りだそうとしている。ハッキングの見解では、人は描写する者 (homo ditector) であり、公の表現の製作者である。その表現は、それを人が使用するときにだけ存在論的な力をもち、使わないときには人はただそれを心に描くだけである。・ ・ ・
　・ ・ ・ カートライトの路線は、論理学はより少なく、戯曲の脚本はより多くそうであるように、基本的な物理学は事実的性質を有するというものである。・ ・ ・
　大雑把にいえば、ハッキングやカートライトのような物理学観によれば、物理学は人間の創造物として理解されねばならず、人々によって使用される文脈において理解されねばならないのであろう。つまり、物理学の哲学を定義する諸問題は、実在的物理学を行なうことの一部として自然に生じてくるとするだろう。(p.28)

　原文は次の通り。

The different works of both Nancy Cartwright and Ian Hacking represent differing reactions to some of the dominant trends in recent philosophy of physics.
　 Ian Hacking's Representing and Intervening is intended to upgrade the role of experiment at the expense of theory in our image of physics, and also to set out an account of Hacking's activist theory of representing as the source of ontological commitment. In Hacking's view, Man is homo depictor, by inner compulsion a maker of public representations which have the ontological force only when he uses them and not when he merely contemplates them. . . .
　 . . . Cartwright thinks of physics as factoidal, as less like logic and more like drama documentary. . . .
　 Broadly speaking, an image of physics like Hacking's or like Cartwright's will have it that one must understand physics as a human creation and in context of its use by people, and that the problems which define the philosophy of physics arise naturally as a part of doing real physics. (p.168f.)

　これは次のような意味だろう。

ナンシー・カートライトとイアン・ハッキングの別々の仕事は、最近の物理学の哲学において支配的な傾向の一部に対する反撥をそれぞれに代表するものだ。
　イアン・ハッキングの『表現と介入』は、我々の物理学のイメージにおける実験の役割を、理論を代償にして、格上げすることに加えて、存在論的関与の源泉としての表象行為についての、彼の実践主義的理論を説明することに向けられている。ハッキングの見解では、人間は内的な衝動により公的な表象をつくる描くヒトであり、そうした表象は、人がそれらを使うときだけ存在論的な力をもち、ただ考えているときにはもたない。・ ・ ・
　・ ・ ・ カートライトは、物理学を論理学よりはドキュメンタリーに似た事実もどきと考えている。・ ・ ・
　大雑把に云えば、ハッキングやカートライトが描くような物理学のイメージは、物理学を、人間の創造物として、人々による使用のコンテクストにおいて理解することを求め、物理学の哲学の領分を劃すような問題は現実の物理学の研究活動の一局面として自ずと生じると主張する。

（ハイデガーなどと違って味もそっけもないいわゆる分析哲学においても、存在ということが問題になる場合には、つまるところやっぱり、存在するとはどういうことなのかが問われているのだと思われるが、しかし、分析哲学では、「存在論」という言葉は、そういう意味で使われることは稀で、普通は、何が存在するのかについての理論を意味したり、あるいは、何が存在するのかについての、ひとの陰伏的 (implicit) な了解のようなものを意味したりするようだ。例えば、何かについて言及するとき、ひとは、何が存在するのかについての自らの陰伏的な了解に陰伏的に基づき、それを話題にのぼせていると考えられないこともない。存在論的関与とは、そのように、存在するとされるものを存在するものとして定立するような陰伏的な行為のことだと云えるかも知れない。もっともその筋の専門家はどう云うか知らないが。）

　ギビンズは、この章を、量子力学の「第一の哲学的成果は、物理学における理論化の限界、物理的世界を表象する我々の力の限界を示している点にある」と結んでいる。

*

　第二章は量子論の解説にあてられている。
　４３ページ目には次のようなくだりがある。

　量子力学の発展前夜にあたる１９２０年代中ごろの、新しい物理学の根本的な状況はなにをもたらしたのか？ 第１に、自然における連続的変化の崩壊がある。これはプランクの法則やボーアの水素原子理論に明示されている。第２に、アインシュタインとド・ブロイが扱ったどちらの放射においても波動と粒子の２重性がある。つまりアインシュタインによる光電効果の説明においても、そして当時は疑わしくさえ思われたのであるが、実質的にはド・ブロイによる物質粒子の波動的観点の立論によっても、それが問題なのである。

　原文は次の通り。

　 What provides the fundamental environment of the new physics in the period of the middle 1920s just before the development of quantum mechanics? First, there is the breakdown of continuous change in Nature, a breakdown which is explicit in Plank's law and in the Bohr theory of hydrogen atom. Second, there is the duality of wave and particle in both radiation, in Einstein's explanation of photoelectric effect, and, though it seemed even more dubious at the time, in matter, via de Broglie's positing of the wave aspect of material particles. (p.24)

　これは次のような意味だろう。

　量子力学の開発直前の１９２０年代中期に、この新しい物理学の基礎的環境を準備したものは何か？ 第一に、自然における連続的変化の崩壊がある。これはプランクの法則やボーアの水素原子理論に明らかだ。第二に、波動と粒子の二元性がある。アインシュタインの光電効果の説明においては、輻射にこの二元性が見られるし、また、当時はさらに疑わしく思われたにせよ、ド・ブロイの物質粒子に対する波動の相の措定によって、物質にもそれが見られる。

　このように量子力学前史の概観を締め括ってから、ギビンズは、簡単な骨組だけを非歴史的に述べると断わった上で、量子力学の解説に入っている。
　４３から４４ページ目にかけてはつぎのようなくだりが在る。

　量子力学のフォーマリズムはミクロ物理系を以下のようにして記述する。
　（１）　系に状態ベクトル（つまりシュレーディンガーの用語でいう波動関数）をあてることによって記述する。状態ベクトルは足したり重ね合わせたりして、新しい状態ベクトルを生むことができる。また
　（２）　系の力学的変数（つまり位置、運動量などのような観測可能量（オブザーバブル））に、一組の状態ベクトルに対応する特定の演算子（オペレーター）をあてることによって記述する。その結果
　（３）　系の状態ベクトルについての知識となんらかのオブザーバブルに対応するオペレーターについての知識から、確率を計算することができる。その値は、その系のオブザーバブルを測定すると、その結果がわれわれの注意深く選択した値域内にあるであろう確率である。

　原文は次の通り。

　 The formalism of quantum mechanics describes microphysical systems:

　 (1) by assigning to them a state-vector (or wave-function in Schrödinger's idiom), and state-vectors can be added or superposed to give new state-vectors; and
　 (2) by assigning to their dynamical variables (or observables, things like position, momentum etc.) certain corresponding operators on the set of state-vectors such that
　 (3) from a knowledge of a system's state-vector and the operator corresponding to any observable one can calculate the probability that a measurement of that observable on the system will have its result in any range we care to choose. (p.25)

　これは、とりまとめれば、次のようなことだろう。

　量子力学のフォーマリズムは、系に状態ヴェクトル（あるいはシュレーディンガーの用語で云えば波動関数）を割り当て、系の力学的変数（つまり位置や運動量等のようなオブザーヴァブル）に状態ヴェクトルの集合上の作用素を割り当てる。系の状態ヴェクトルとオブザーヴァブルに対応する作用素に関する知識から、その系について件のオブザーヴァブルを測定した結果の値が任意に撰んだ範囲に含まれる確率を計算できる。また状態ヴェクトルを足し合わせれば、つまり重ね合わせれば、新たな状態ヴェクトルが得られる。

　この最後に述べられていることがらは重ね合わせ原理と呼ばれる。
　それに続いて、４４から４５ページ目にかけては次のようなくだりがある。

　状態ベクトルとは、量子系についての真なるもの、すなわちその状態についての真なるものの数学的表現である。オペレーターとは、状態ベクトルに掛け合わせて、通常はもとの状態ベクトルとは異なる状態ベクトルを生むものである。すなわちこの状態ベクトルは、もとの状態ベクトルの単なる倍数ではない。・ ・ ・
　量子力学のフォーマリズムと古典力学のそれとが、いかに直接的な関連をもたないかに注目しよう。・ ・ ・ 量子力学の場合では、力学的変数の値はある量子状態の記述においてオペレーターが及ぼす作用に結びつけられる。・ ・ ・
　しかし、古典力学と比較した場合、量子力学の根本的な奇妙さはつぎのことに見られる。
　（４）　力学的変数に対応するあるオペレーターの対 A 、B は、交換することができない。すなわち、積 AB は積 BA に等しくない。
　このことは、大雑把にいえば二つのオペレーターが必ずしも同時確定的な値をもつ必要はないことを意味する。・ ・ ・ この非可換性 (non-commutativity) を拡大解釈すれば、それはわれわれが論争の的となる解釈要素を導入するということになる。

　原文は次の通り。

　 A state-vector is a mathematical representation of what is true of a quantum system, that is of its state. An operator is something that multiplies into a state-vector yielding a state-vector, usually different from, that is not a numerical multiple of, the original state-vector. . . .
　 Note how much more indirect is the interpretation of formalism of quantum mechanics compared with that of classical mechanics. . . . In the quantum mechanical case the values of dynamical variables are associated with the effect of an operator on a quantum state description.
　 But the fundamental oddness of quantum mechanics in comparison with classical mechanics is that:

　 (4) certain pairs of operators A, B corresponding to dynamical variables fail to commute, that is AB is not equal to BA.

　 This means roughly that the two operators need not always have simultaneous determinate values. . . . To give noncommutativity the gloss we do is to introduce a controversial element of interpretation. (p.25f.)

　これは次のような意味だろう。

　状態ヴェクトルは、量子系について成り立つことがら、つまり量子系の状態の数学的表現だ。作用素は、状態ヴェクトルに掛けられて、普通は、もとの状態ヴェクトルとは別の、つまりもとの状態ヴェクトルに数を掛けたものではない状態ヴェクトルを生むものだ。・ ・ ・
　量子力学のフォーマリズムの解釈が、古典力学の場合に比べて、いかに非直接的かに注意せよ。・ ・ ・ 量子力学の場合、力学的変数の値は量子状態の記述に対する作用素の作用に結びつけられる。
　しかし、古典力学に比べての、量子力学の根本的な奇妙さは、次の点に在る。

　（４）　特定の力学的変数に対応する作用素 A と B の対は非可換だ。つまり AB は BA に等しくない。

　これは、大雑把に云えば、ふたつの作用素［によって表わされるオブザーヴァブル］が常に同時確定的な値をもつとは限らないことを意味する。・ ・ ・ 非可換性にこうした注釈を付けることは、論争の種になる解釈を招き入れるに等しい。

　作用素とは、この場合、状態ヴェクトルを状態ヴェクトルに対応づける写像のことであり、「AB 」や 「BA 」は合成写像（つまり二重の対応づけ）を意味する。また、この文脈では、合成写像は積と呼ばれる。
　４５から４６ページ目にかけては次のようなくだりがある。

オペレーターは掛け合わせて新しいオペレーターをつくることができるのだから、オペレーターは代数を形成することがわかる。このことで奇妙なのは、それが一般に非可換的な代数であることである。二つのオペレーター A と B は、状態ベクトル f に作用して

A (Bf ) ≠ B (Af )

したがって、

AB ≠ BA

となるような場合は交換することが許されない。
　本当に興味深いのは、位置についての X 、運動量についての P_x という基本的なオペレーター対の場合である。これらのオペレーターについては、

XP_xf = P_xXf

となるような状態ベクトルは存在しない。事実、差 XP_x - P_xX は（奇妙にも）、マイナス１の平方根に（２πで割った）プランク定数をかけた一定値 となる。言い換えれば、交換子 X と P_x 、すなわち（XP_x - P_xX ）をただ略記したものである [X, P_x] は、（X と P_x の領域、および XP_x と P_xX の領域における）どんな状態ベクトル f に対しても、つぎのような結果になる。

[X, P_x]f = (XP_x - P_xX )f = f

・ ・ ・ 　ゆえに、二つの重要な帰結が量子力学のフォーマリズムから生ずる。
（５）　ΔX と ΔP_x の標準偏差（すなわち拡がり）として、

ΔX ・ΔP_x ≧ /2

が帰結する。・ ・ ・
（６）　もし状態ベクトルが X の値の有限値域外では消えてしまうのであれば、その状態ベクトルは P_x について局所化することができず、またその逆もいえる。

原文は次の通り。

Operators can be multiplied to form new operators and so it turns out that operators form an algebra. The odd thing about it is that it is generally a noncommutative algebra. Two operators A and B fail to commute if and only if there is a state-vector v such that

A (Bv ) ≠ B (Av )

so that

AB ≠ BA.

　 The really interesting case is that of the pair of fundamental operators X, for position, and P_x , for momentum. For them, there is no state-vector v such that

XP_xv = P_xXv.

　 In fact, the difference XP_x - P_xX is (oddly) a constant , the square root of minus one times Planck's constant (divided by 2π). In other words, [X, P_x], the commutator of X and P_x which is just shorthand for （XP_x - P_xX ), has the following effect on any state-vector v (in the domain of X and P_x and of XP_x and P_xX )

[X, P_x]v = (XP_x - P_xX )v = v.

. . .
　 Two important consequences then follow within the formalism of quantum mechanics.

　 (5) For the standard deviation (or spreads) δX and δP_x :

δX ・δP_x ≧ /2

. . .
　 (6) if a state-vector vanishes except within a finite range of values of X, then it is unlocalizable in P_x and vice versa. (p.26f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

作用素を掛け合わせれば新たな作用素が得られる。よって、作用素は代数を成すことがわかる。奇妙なのは、それが一般に非可換代数だということだ。ふたつの作用素 A 、B が非可換なのは、或る状態ヴェクトル v が在って

A (Bv ) ≠ B (Av )

よって

AB ≠ BA

となる場合であり、その場合に限る。
　本当に興味深いのは、位置についての X と運動量についての P_x という基本的な作用素の対の場合だ。これらについては

XP_xv = P_xXv

となるような状態ヴェクトルv は存在しない。
　実際、差 XP_x - P_xX は、（奇妙なことに） -1 の平方根に（2πで割った）プランク定数をかけた定数 だ。［i = -1、 = h/2π、h はプランク定数。］云い換えれば、X と P_x の交換子 [X, P_x] 、これは XP_x - P_xX の単なる略記だが、この交換子は、（XP_x と P_xX 両方の定義域に属する）どんな状態ヴェクトル v についても、次のように作用する。

[X, P_x]v = (XP_x - P_xX )v = v

・ ・ ・
　ふたつの重要な帰結が量子力学のフォーマリズムにおいて得られる。

　（５）　標準偏差（つまり拡がり）ΔX 、ΔP_x について、

ΔX ・ΔP_x ≧ /2

・ ・ ・
　（６）　或る状態ヴェクトル［つまり波動関数］が X の値の有限の範囲の外ではゼロになる場合、その状態ヴェクトルは P_x に関して局所化できず、逆もまた成り立つ。

　この（６）は胡乱な云い方に思えるが、それは措くとする。
　４９ページ目には次のようなくだりがある。

位置と運動量は、古典力学の基礎であるように、ある意味では量子力学の基礎となっている。事実、X と P_x との交換関係 (commutation relation) を量子力学の基本法則と考えることもできるのである。
　さらに、オペレーター X と P_x から、対応する古典的な表現を用いて角運動量のような他の量子力学のオペレーターを導くことができる。ゆえに z 方向の角運動量 L_z は、

L_z = XP_y - P_yX

　ここでわれわれは一般化した対応原理を用いている。これは量子力学のフォーマリズムを古典力学に基づいて使用する方法である。

　原文は次の通り。

　 Position and momentum are, in a sense, basic in quantum mechanics just as they are in classical mechanics. In fact, one can take the commutation relation for X and P_x to be the fundamental law of quantum mechanics.
　 One can then derive the other quantum-mechanical operators, like angular momentum, from the operators X and P_x using the corresponding classical expressions. Thus angular momentum in z -direction L_z is just

L_z = XP_y - P_yX.

Here we use a kind of generalized correspondence principle. Here is a way in which the use of the quantum-mechanical formalism is dependent on classical mechanics. (p.29)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　位置と運動量は、或る意味では、古典力学の場合と同様、量子力学においても基礎的だ。実際、X と P_x についての交換関係を量子力学の基本法則とみなし得る。
　角運動量のような他の量子力学的作用素は、それに対応する古典論的表現を利用して、作用素 X と P_x から導びける。例えば、z 方向についての角運動量 L_z は

L_z = XP_y - YP_x

ここで、我々は、或る種の一般化された対応原理を用いている。量子力学的フォーマリズムの行使にはこのように古典力学に依存する面がある。

　ギビンズは説明を加えていないが、この場合の交換関係とは、次のような一連の関係のことだ。

[X, Px] =

[Y, Px] = 0

[Z, Px] = 0

[X, Py] = 0

[Y, Py] =

[Z, Py] = 0

[X, Pz] = 0

[Y, Pz] = 0

[Z, Pz] =

[X, X ] = 0

[Y, X ] = 0

[Z, X ] = 0

[X, Y ] = 0

[Y, Y ] = 0

[Z, Y ] = 0

[X, Z ] = 0

[Y, Z ] = 0

[Z, Z ] = 0

[Px , Px] = 0

[Py , Px] = 0

[Pz , Px] = 0

[Px , Py] = 0

[Py , Py] = 0

[Pz , Py] = 0

[Px , Pz] = 0

[Py , Pz] = 0

[Pz , Pz] = 0

（ただし、この場合、「」は、数ではなく、それぞれのヴェクトルに数 を掛ける作用素を表わし、「0」は凡てのヴェクトルをゼロヴェクトルに対応づけるゼロ作用素を表わす。）これらを公準として採り、それによって位置および運動量作用素を規定し、さらにそれらから、対応原理に訴えて、他の作用素を導く、というふうに進むことが出来る訳で、その意味で、交換関係は基本法則と考えられるということなのだろう。

　５０から５１ページ目には次のようなくだりがある。

われわれは量子系の可能な状態を、位置 x の関数である状態ベクトルで表わすことにした。ではわれわれは、いかにしてオペレーター X と P_x にたどり着くのか？
　X を一方向の位置ベクトル x で表わすことは理にかなっているように思われる。では P_x についてはどうか？ 交換関係に眼を向けると、X と P_x が関数に作用するオペレーターであることを思い起せば、通常のどんな関数 f についても、

[X, P_x]f = (XP_x - P_xX )f =

がえられる。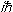
　P_x( ) の代わりに (-d /dx )( ) を代入すれば、交換関係を満足していることがわかる。したがってわれわれは、-d /dx をオペレーター P_x の表現であるとみなす。
　・ ・ ・ V で与えられる場のポテンシャル内を運動量 p で動いている１個の１次元の古典粒子は、

E = p ²/2m +V

で与えられるエネルギー E をもつ。したがって量子力学のエネルギー・オペレーター E は、

E = (-²/2m )(d ²/dx ²) +V

で与えられる。
　このオペレーターは f のような関数に作用する。そしてシュレーディンガー方程式によれば、

(-²/2m )(d ²/dx ²)f +Vf = ef

ただし e は許され安定した、かつ一定のエネルギー準位、すなわちエネルギー固有値であり、f はエネルギー固有状態であり、シュレーディンガー方程式を満足する。

　原文は次の通り。

　 We choose to represent the possible states of a quantum system as state-vectors which are functions of position x. How can we arrive at the operators X and P_x ?
　 It seems reasonable that we represent X by the position vector x, in one dimension. What then of P_x ?
　 Turning to the commutation relation, remembering that X and P_x are operators acting on functions, we have

[X, P_x]f = (XP_x - P_xX )f = f

for any reasonable function f.
　 Substituting P_x = -d /dx we see that the commutation relation is satisfied. So we take -d /dx as the representation of the operator P_x .
　 . . . A classical particle moving with momentum p in a field potential given by V has energy E given by

E = p ²/2m +V.

So the quantum mechanical energy operator E is given by

E = (-h ²/2m )(d ²/dx ²) +V.

This operator acts on function like f. The Schrödinger equation tells us that

(-h ²/2m )(d ²/dx ²)f +Vf = ef

where e ranges over the allowed stable and definite energy levels or energy eigenvalues and the f s which satisfy the Schrödinger equation are the energy eigenstates. (p.29f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　我々は量子系の在り得る状態を、位置 x の関数である状態ヴェクトルによって表わすことにしたい。作用素 X と P_x には、どうすれば辿り着けるか？
　一次元において X を位置ヴェクトル x によって表わすのは妥当に思われる。P_x についてはどうなるか？
　交換関係に訴えて、X と P_x が関数に作用する作用素であることを考えれば、適当な関数 f について、

[X, P_x]f = (XP_x - P_xX )f = f

　P_x= -d /dx とすれば、交換関係［[X, P_x] = ］が充たされるのがわかる。そこで我々は、-d /dx を作用素 P_x の表現とみなす。
　・ ・ ・ ポテンシャル V の場の中を運動量 p で動くひとつの古典論的粒子は

E = p ²/2m +V

として規定されるエネルギー E をもつ。そこで、量子力学的エネルギー作用素 E は

E = (-²/2m )(d ²/dx ²) +V

として規定される。この作用素は f のような関数に作用する。［いわゆる定常状態に関する一次元の］シュレーディンガー方程式とは次の通り。

(-²/2m )(d ²/dx ²)f +Vf = ef

e は許される一定のエネルギー準位あるいはエネルギー固有値を表わしており、この方程式を充たす f は［固有値 e に対応する］エネルギー固有状態だ。

　５１ページ目には続いて次のようなくだりがある。

　固有値および固有状態という概念は、一般にすべてのオブザーバブルに適用する。ゆえに関数 f が固有値 o_n をもつオペレーター O の固有状態となるのは、

Of = o_nf

となる場合のみである。・ ・ ・ ある系が力学的変数に対して確定値をもつのは、その系が対応するオペレーターの固有状態にある場合にのみであり、固有値が固有状態に結びつけられて確定値となるのである。この考え方には異論の余地がない。

　原文は次の通り。

　 The ideas of eigenvalue and eigenstate apply generally to all observables. Thus a function f is an eigenstate of an observable O with eigenvalue o_n if and only if

Of = o_nf.

. . . a system has a definite value for a dynamical variable if and only if it is in an eigenstate of the corresponding operator, the definite value being the eigenvalue associated with the eigenstate. It is not an uncontroversial idea. (p.30)

　これは次のような意味だろう。

　固有値および固有状態というアイディアは、すべてのオブザーヴァブルに当てはまる。関数［状態ヴェクトル］ f が固有値 o_n をもつオブザーヴァブル O の固有状態であるのは

Of = o_nf

となる場合であり、またその場合に限る。・ ・ ・ ひとつの系が或る力学的変数について確定値をもつのは、それが対応する作用素の固有状態にある場合であり、その場合に限る。確定値はその固有状態に結びついた固有値だ。この考え方には議論の余地がない訳ではない。

　この、オブザーヴァブルの確定値と固有状態との関係は固有値固有状態リンクと呼ばれる。
　５２から５４ページ目には次のようなくだりがある。

　状態 f を取り上げ、これに A を作用させると Af が得られる。次に積 Af を f の複素共役数で、つまり f ^* で積分する。最後にこれを (f ^*)f の積分で割る。これで状態 f における A の期待値が与えられる。それはこう書ける。

<A > =∫f ^*(Af )dx /∫f ^*fdx

この表記を有意味にするためには、f が２乗可積［平方積分が可能］であるか、さもなければ分母が無限でなければならない。・ ・ ・
　われわれはさらに進めて期待値についての表記を単純化することができる。状態ベクトルを規格化すれば、

∫f ^*fdx = 1

したがって、

<A > =∫f ^*(Af )dx

規格化が含意しているのは定数による掛け算ということにすぎず、したがって固有値や期待値に影響を及ぼすことができないことは容易にわかる。したがって、われわれはこの単純化された表記、つまり規格化された固有状態の表記を採用して、われわれの量子力学アルゴリズムとすることにしよう。・ ・ ・
　最後になるが重要な事実がある。それは、われわれが本書で考察する例において、与えられたオブザーバブルの異なる二つの状態はすべて、内積がゼロになる (orthogonal) ことである。二つの固有状態の内積がゼロになるのは、それらが「直交」しているとき、言い換えれば、

∫f ^*gdx = 0

のときである。x に関する f ^* の g 倍の積分はスカラー積のようになる。・ ・ ・ 一組の状態ベクトルはまさにベクトル空間の構造をもっており ・ ・ ・

　原文は次の通り。

　 Take the state f and operate it with A, getting Af. Then integrate the product of Af with the complex conjugate of f, namely f ^*. Finally divide this by the integral of (f ^*)f. This gives you the expectation-value of A in the state f. One writes

<A > =∫f ^*(Af )dx /∫f ^*fdx.

　 For this expression to make sense f must be square-integrable, otherwise the denominator will be undefined. . . .
　 We can go further and simplify the expression for the expectation-value if we normalize state-vectors so that

∫f ^*fdx = 1

so that

<A > =∫f ^*(Af )dx.

It is easy to see that normalization involves no more than a multiplicaion by a constant and so cannot affect eigenvalues or expectation-values. So we let this simplified expression, with normalized eigenstates, be our version of the quantum-mechanical algorithm. . . .
　 One last but important fact. In all the examples we consider in this book two different eigenstates of a given observable are orthogonal. Two eigenstates are orthogonal when they are at ‘right-angles’, when in other words

∫f ^*gdx = 0.

The integral of f ^* time g over x behave like a scalar product. . . . It turns out that the set of state-vectors has exactly the structure of a vector space. . . .(p.31f.)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　状態 f をとって、A を作用させれば Af が得られる。そこで、f の複素共役 f ^* と Af の積を積分する。最後にそれを f ^*f の積分で割る。これで状態 f についての A の期待値が得られる。それを次のように表記する。

<A > =∫f ^*Af dx /∫f ^*fdx

この表現が意味をもつには、f が平方積分可能［∫f ^*fdx ＜∞］でなければならない。そうでなければ分母が定まらないことになる。・ ・ ・
　さらに、期待値の表現は単純化できる。状態ヴェクトルを

∫f ^*fdx = 1

となるように規格化すれば、

<A > =∫f ^*Afdx

規格化は定数倍を伴うだけで、固有値や期待値に影響しないことは容易に判る。そこで、規格化された状態ヴェクトルを用い、この単純化された表現を、我々のヴァージョンの量子力学的アルゴリズムとする。・ ・ ・
　最後に重要な事実をひとつ。本書で考察する凡ての例において、所定のオブザーバブルの異なるふたつの固有状態は直交している。ふたつの状態ヴェクトル f 、g が直交するのは、それらが「直角をなす」場合、云い換えれば、

∫f ^*gdx = 0

となる場合だ。x についての f ^* の g 倍の積分はスカラー積のように振る舞う。・ ・ ・ 状態ヴェクトルの集合は厳密にヴェクトル空間の構造をもつことが判る ・ ・ ・

　つづいて、電子のスピンに関する作用素と状態ヴェクトルの例が示される。
　スピンはヴェクトル量だが、その成分のとり得る値は、電子のようないわいるスピン 1/2 の系の場合、/2 か -/2 のどちらかしかない。それで、電子のスピンは、どんな方向をとっても、その方向について正反どちらかの向きしかとらない、というような云い方をされることが多いようだ。ここではその正反が「上向き」および「下向き」と表わされている。
　５６から５９ページ目にかけては次のようなくだりがある。

　したがってわれわれは単純に、電子はどの任意の方向においてもスピン「上向き」か「下向き」をもっていることを受け入れよう。それゆえに、スピンを記述する状態ベクトルは二つの成分しかもたない。電子を記述する状態ベクトル一般は、第１にスピンをもたない状態ベクトルと第２にスピンについての状態ベクトルとの積になるであろう。どの方向 z に対しても、スピン部分についての状態ベクトルは、z スピン「上向き」と z スピン「下向き」の重みの和でなければならない。この重みの２乗の和は１になる。
　スピンを扱うために、われわれは一般化した対応原理に訴える。座標 x 、y 、z および運動量 P_x 、P_y 、P_z をもつ１個の古典粒子は、

L_z = XP_y - YP_x

で与えられる角運動量 L_z という z 成分をもっている。x 成分の L_x および y 成分の L_y は x、y、z を入れ換えた式から得ることができる。ここで、P_x の代わりに-d/dx を代入するなどすれば、角運動量 L_x 、L_y 、L_z についての量子力学的表記が得られる。そして、次の交換関係

[L_x - L_y] = L_z

が保持されていることを確認することができる。・ ・ ・
　われわれはいかにして「スピン」というオブザーバブルの成分に対応するオペレーター S_x 、S_y 、S_z を表記することができるだろうか？ パウリのスピン・マトリクスを使って、というのが答えである。すなわち、 S_x の代わりに (1/2)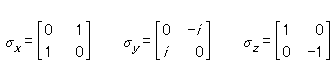σ_x を代入するなどすれば、交換関係

[S_x - S_y] = S_z

などがスピンの角運動量についても満足されていることがわかる。
　２×２マトリクスで表記されるスピンの角運動量オペレーターとともに、スピン状態は２要素のカラム・マトリクス［縦マトリクス］で表記される。
　z 方向にスピン「上向き」をもつ１個の電子についての状態ベクトル |z, +> はどうか？ われわれが得るのは、

S_z|z, +> = + (/2)|z, +>

であり、また「上向き」については「上段」、「下向き」については「下段」の二つの成分の２乗の和は１でなければならないので、 同様に、スピン「下向き」については、 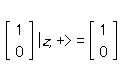　より興味深い問いは、x 方向にスピン「上向き」である１個の電子は |z, +> と |z, -> を使ってどのように表わされるか、である。 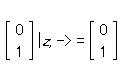であるとしよう。 |x, +> は、x 方向にスピン「上向き」である１個の電子の状態ベクトルである。われわれが問うているのは、この状態ベクトルを z 方向にスピン「上向き」とスピン「下向き」の重ね合わせによってどう表わすべきか、である。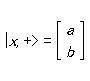

S_x|x, +> = + (1/2)|x, +>

であるので、 したがってわれわれは a = b を選択することができる。規格化を用いれば a = b = 1/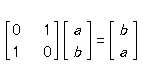2 が得られる。
　σ_y についてパウリ・スピン・マトリクスを用いると、|y, +> は z 方向にスピン「上向き」と「下向き」によって次のように表記することができる。 状態ベクトルの確率解釈を用いれば、もし１個の電子が z 方向にスピン「上向き」をもっていれば、y 方向のスピン測定後にこの電子がスピン「上向き」でみつかる確率は、|1/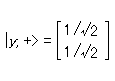2|² = 1/2 であるといえる。

　原文は次の通り。

　 So we simply accept that in any chosen direction an electron has spin ‘up’ or ‘down’. Therefore the state-vector which describes spin has only two components. The overall state-vector which describes an electron will be a product of first a nonspin state-vector and secondly the state-vector for spin. For any chosen direction z, state-vector for the spin part must be a weighted sum of z -spin ‘up’ and z -spin ‘down’, the sum of the squares of the weights being 1.
　 To treat spin we appeal to the generalized principle of correspondence. A classical particle with coordinates x, y and z, and momenta P_x , P_y , P_z has its z -component of angular momentum L_z given by

L_z = XP_y - YP_x .

　 One can get the x - and y -components L_x and L_y from the equation by permuting x, y and z. Substituting P_x = -d/dx, etc. one can then obtain the quantum-mechanical expressions for the angular momenta L_x , L_y and L_z . Furthermore one can verify that the following commutation relation holds

[L_x - L_y] = L_z .

. . . 　 How can we represent the operators S_x , S_y , S_z corresponding to the components of the observable ‘spin’? The answer is: by means of the Pauli spin matrices which are: If you substitute S_x = (1/2)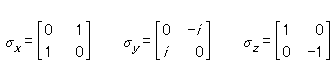σ_x etc. then you can see that the commutation relations

[S_x - S_y] = S_z , etc.

for spin angular momentum are satisfied.
　 With the spin angular momentum operators represented by 2-by-2 matrices, the spin states are represented by column matrices with 2 elements.
　 What is the state-vector |z, +> for an electron having spin ‘up’ in the z -direction?
　 Since we must have S_z|z, +> = + (1/2)|z, +> then, since the sum of the squares of the two components ‘upper’ for ‘up’ and ‘lower’ for ‘down’ must be unity, we have Similarly for spin ‘down’ you get 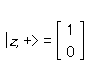　A more interesting question is: what is the representation in terms of |z, +> and |z, -> for an electron whose spin is ‘up’ in the x -direction?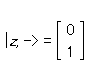
　 Let 　The term |x, +> is the state-vector for an electron whose spin is ‘up’ in the x -direction. We are asking how we should represent this state-vector in terms of a superposition of spin ‘up’ and spin ‘down’ in the z -direction.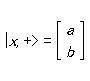
　 As S_x|x, +> = + (1/2)|x, +> and hence we can choose a = b. Using normalization we have a = b = 1/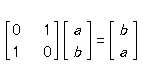2.
　 Using the Pauli spin matrices you can (and should) show that one can represent |y, +> in terms of spin ‘up’ and ‘down’ in the z -direction as 　 Using the probability interpretation of the state-vector one can say that if an electron has spin ‘up’ in the z -direction the probability that it will be found to have spin ‘up’ in the y -direction after a measurement of spin in the y -direction will be |1/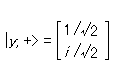2|² = 1/2, that is 1/2. (pp.33-35)

　これは次のような意味だろう。（ただし、適宜修正を加えた。）

　そこで、どんな方向をとっても、電子はその方向について「上向き」か「下向き」のスピンをもつことをあっさり受け容れる。したがって、スピンを記述する状態ヴェクトルはふたつの成分しかもたない。電子を記述する総体的な状態ヴェクトルは、スピンに関わらない状態ヴェクトルとスピンに関する状態ヴェクトルの積になる。どんな方向 z についても、スピン部分に関する状態ヴェクトルは、「上向き」の z スピンと「下向き」の z スピン［状態を表わすヴェクトル］の重み付き和でなければならず、それらの重みの平方［つまり絶対値自乗］の和は１だ。
　スピンを扱うために、一般化された対応原理に訴える。［直交］座標 x 、y 、z および運動量 P_x 、P_y 、P_z をもつ古典論的粒子は

L_z = XP_y - YP_x

として規定される角運動量の z 成分 L_z をもつ。
　x 成分 L_x および y 成分 L_y は、この等式から、x 、y 、z を［巡回］置換することによって得られる。そこで、P_x = -d/dx 等々とすれば、角運動量 L_x 、L_y 、L_z に対する量子力学的表現が得られ、交換関係

[L_x - L_y] = L_z

が成り立つことが判る。・ ・ ・
　「スピン」というオブザーヴァブルの x 、y 、z 成分に対応する作用素 S_x 、S_y 、S_z はどうすれば表現できるか？ 次に挙げるパウリ・スピン・マトリクスによって、というのが答だ。 S_x = (1/2)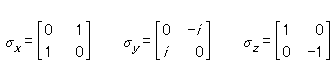σ_x 等々とすれば、スピン角運動量に関する交換関係

[S_x - S_y] = S_z

等々が充たされることがわかる。
　スピン角運動量作用素が２×２マトリクスによって表わされるのに対して、スピン状態は２要素の列マトリクスによって表わされる。
　z 方向について「上向き」のスピンをもつ電子に対する状態ヴェクトル |z, +> は何か？
　S_z|z, +> = + (1/2)|z, +>［つまり |z, +> は S_z の固有値 + (1/2) に対応する固有ヴェクトル］でなければならず、また、「上段」と「下段」の成分の平方の和は１でなければばらない［つまり規格化されていなければならない］ので、 同様に、「下向き」のスピンについては 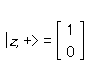　より興味深いのは、x 方向について「上向き」のスピンをもつ電子の |z, +> と |z, -> による表現はどうなるかということだ。 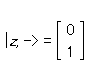としよう。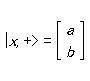
　|x, +> は、x 方向について「上向き」のスピンをもつ電子の状態ヴェクトルだ。問題は、この状態ヴェクトルを、z 方向について「上向き」と「下向き」のスピン［状態を表わすヴェクトル］の重ね合わせによってどう表わすか、ということだ。
　S_x|x, +> = + (1/2)|x, +> であり、また、 よって、a = b。規格化すれば、a = b = 1/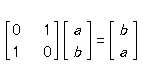2。［したがって、|x, +> = (1/2)|z, +> + (1/2)|z, ->。］
　|y, +> は、z 方向について「上向き」および「下向き」のスピン［状態を表わすヴェクトル］によって、次のように表わせることが、パウリ・スピン・マトリクスを使って示せる。（これを示してみよ。） 　状態ヴェクトルについての確率解釈を用いれば、ひとつの電子が z 方向について「上向き」のスピンをもつ場合、y 方向についてのスピンの測定の結果、その電子が y 方向について「上向き」のスピンをもつのが見出される確率は、|1/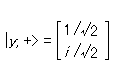2|²、つまり 1/2 だと云える。

　これらの状態ヴェクトルは、二次元複素ヴェクトル空間 C² のヴェクトルだ。スカラー倍 λv および和 v + w は次のように定義される。 として、 一方、複素数を成分とする２×２マトリクスは C² 上の作用素であり、その作用は次のように規定される。 として、 　また、C² においては、標準的な内積 <v, w > が次のように定義される。 として、

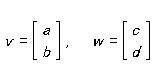
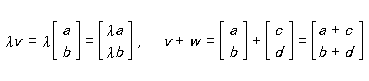
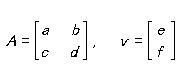
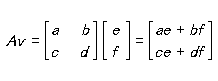
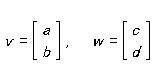
<v, w > = a^*c + b^*d

ただし「 ^*」は複素共役をとる演算を表わす。さらに、ノルム ||v || が

||v || = <v, v >

として定義される。||v || = 1 となるヴェクトル v は単位ヴェクトルと呼ばれるが、ゼロヴェクトルでないヴェクトル w に 1/||w || を掛けて単位ヴェクトルを得る操作が規格化だ。
　電子のようなスピン 1/2 の系のスピンの x 、y 、z 方向についての状態ヴェクトルをまとめてみれば以下の通り。
　最後の段落に出て来る確率の値は、|z, +> を |y, +> と |y, -> によって

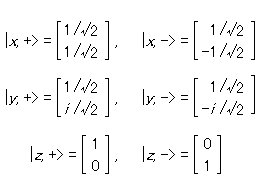
|z, +> = (1/2)|y, +> + (1/2)|y, ->

というふうに展開して、|y, +> の係数の絶対値自乗――したがってこの場合は単に自乗――をとることで得られる。

２００３年１月　　大熊康彦

---

雑録　／　『量子論理の限界』について ( I ) ( II ) ( III ) ( IV ) ( V )