論理哲学論考　1-7　4.1-4.5　4.41-4.46
 　　　　 
4.44 件の符号「W」と諸真理可能性の対応づけによって生じる記号はひとつの文記号だ。
4.441 記号「W」と「F」の複合体に対応する対象（または諸対象の複合体）など無いことは明らかだ。それは横線と縦線や括弧に対応するものなど無いのと同断だ。――「論理的対象」などというものは存在しない。
同様のことは、もちろん、「W」と「F」の図式と同じことを表現する総ての記号に当てはまる。
4.442 例えば、これは文記号だ。
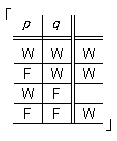table2
（フレーゲの「判断線」「Urteilstrich」は論理的に全く無意義〔bedeutungslos〕だ。それは、フレーゲ（とラッセル）のもとでは、ただ、これらの著者がそうして表示された文を真だと考えるということを呈示するだけだ。「Urteilstrich」は、だから、例えば文の番号と同様、文構造には属さない。ひとつの文が自らについて、それが真だと言明することなどあり得ない。）
件の図式における真理可能性の順番がひとつのコンビネーション規則によってはっきり定められていれば、最後のコラムはそれだけでもう当の諸真理可能性の表現だ。そのコラムを列として書けば、先の文記号は
「(W W - W)(p, q )」
あるいは、もっとはっきり
「(W W F W)(p, q )」
となる。
（左側の括弧の中の座の数は右側の括弧の中の項の数によって規定される。）