| 6.12 |
論理の文全般がトートロジーであること、それは言語の、世界の形式的――論理的――属性全般を示す。 論理の文の諸成分がそのように関聯づけられてトートロジーになることは、当の諸成分の論理を特徴づける。 諸文が特定の仕方で関聯づけられてトートロジーになるためには、それらが特定の構造的諸属性をもっている必要がある。それらがそのように結びつけられてトートロジーになることは、だから、それらがそうした構造的諸属性を有していることを示している。 |
| 〔6.120 という番号をもつ文は存在しない。〕 | |
| 6.1201 | 例えば、文「p 」と「〜p 」が「〜(p . 〜p )」という結びつきでトートロジーになることは、それらが互いに矛盾することを示している。文「p ⊃ q 」、「p 」、「q 」が「(p ⊃ q ) . (p ) : ⊃ : (q )」という形式に結び合わされてトートロジーになることは、q が p と p ⊃ q から帰結することを示しており、「(x ) . fx : ⊃ : fa 」がトートロジーであることは fa が (x ) . fx から帰結することを、等々。 |
| 6.1202 | ひとが、同じ目的のために、トートロジーではなくコントラディクションを用いることもできただろうことは明らかだ。 |
| 6.1203 |
トートロジーをそういうものとして認識するために、ひとは、当のトートロジーに一般性表示が現われないケースでは、次のような具体的方法を利用することができる。私は「p 」、「q 」、「r 」等に代えて「W p F」、「W q F」、「W r F」等と書く。特定の諸真理コンビネーションを私は括弧によって、例えば、
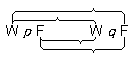 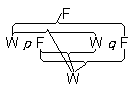 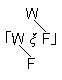 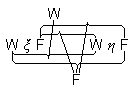 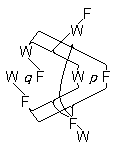 |
論理哲学論考 1-7 6.1-6.5 6.11-6.13