雑録 / 都市はセミラティスではない
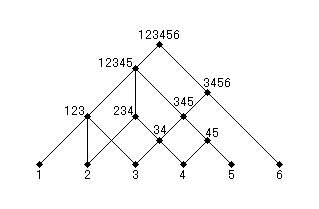
図3 集合 { 1 }, { 2 }, { 3 }, { 4 }, { 5 }, { 6 }, { 3, 4 }, { 4, 5 }, { 1, 2, 3 }, { 2, 3, 4 }, { 3, 4, 5 }, { 3, 4, 5, 6 }, { 1, 2, 3, 4, 5 }, { 1, 2, 3, 4, 5, 6 } の全体は包含関係の順序に関して順序集合を成す。このダイアグラムはそれを表わしている。(ちなみに、2 の結節点からの上向きの――下に回り道をすることなく上方に向かう――径路には 2→123→12345→123456 と 2→234→12345→123456 のふたつ、3 からは 3→123→12345→123456、3→34→234→12345→123456、3→34→345→12345→123456、3→34→345→3456→123456 の四つが在って、2 からの径路と 3 からの径路の交点となっている結節点は全部で四つ在る。これらの交点のうち 123 と 234 のどちらからも残りの交点 12345 および 123456 へと上向きの径路が通じているが、123 と 234 を繋ぐ径路は存在しない。これは { { 2 }, { 3 } } の上限が存在しないことを意味し、したがって、この順序集合は有限集合上半束ではない。) 
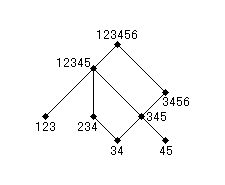
図4 集合 { 3, 4 }, { 4, 5 }, { 1, 2, 3 }, { 2, 3, 4 }, { 3, 4, 5 }, { 3, 4, 5, 6 }, { 1, 2, 3, 4, 5 }, { 1, 2, 3, 4, 5, 6 } の全体は有限集合上半束を成す。(例えば、123 からの上向きの径路はひとつ、34 からは三つ在って、123 からの径路と 34 からの径路の交点となっている結節点は全部でふたつ在るが、その交点のひとつ 12345 からの上向きの径路はもうひとつの交点 123456 に通じている。これは { 1, 2, 3, 4, 5 } が { { 1, 2, 3 }, { 3, 4 } } の上限であることを意味する。) 
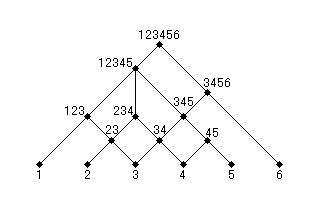
図5 集合 { 1 }, { 2 }, { 3 }, { 4 }, { 5 }, { 6 }, { 2, 3 }, { 3, 4 }, { 4, 5 }, { 1, 2, 3 }, { 2, 3, 4 }, { 3, 4, 5 }, { 3, 4, 5, 6 }, { 1, 2, 3, 4, 5 }, { 1, 2, 3, 4, 5, 6 } の全体は有限集合上半束を成す。(図3の順序集合は { { 2 }, { 3 } } の上限が存在しないため有限集合上半束ではないが、こちらの順序集合では { 2, 3 } がその上限となっている。) 
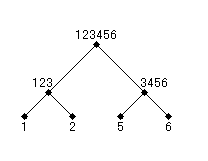
図6 集合 { 1 }, { 2 }, { 5 }, { 6 }, { 1, 2, 3 }, { 3, 4, 5, 6 }, { 1, 2, 3, 4, 5, 6 } の全体はツリーを成す。 