論理哲学論考　1-7

---

論理哲学論考

ルートヴィヒ・ヴィトゲンシュタイン

亡友デイヴィド・Ｈ・ピンセントに捧ぐ

モットー： ・ ・ ・ そして、ひとが、ただざわめきとどろくのを聞いたのではなくて、諒解していることがらの総ては、三つの言葉で述べられ得る。

――キュルンベルガー

*　 　*　 　*　 　*　 　*　 　*　 　*

緒言

　この本が解るのは、おそらくは、ここに表明されている考え――というか似たような考え――を嘗て自ら考えたことがある者だけだろう。――これは、だから、教科書ではない。――その狙いは、誰か理解をもって読む者に歓びを齎したとき、遂げられることだろう。
　この本は哲学的問題全般を扱っており、それらの問題設定が我々の言語の論理に対する誤解に基くことを明らかにしている――そう私は信じる。ひとはこの本の大意を例えばこんな言葉で捉えることができるだろう： そもそも述べられ得ることがらは明確に述べられ得るし、また、話すことができないことがらについては、ひとは黙らなければならない。
　この本は、そこで、考えることにひとつの境界を劃そうとする。より正確には――考えることにではなく、考えの表現にだ。考えることに何らかの境界を劃すには、我々はその境界の両側を考えることができなければならない（故に考えられ得ないことがらを考えることができなければならない）だろうから。
　その境界は、だから、言語の中でだけ劃され得るだろうし、その向う側に位置するものは単なるナンセンスだろう。
　私は自らの努力がどれだけ他の哲学者たちのものと重なり合うのかを判定するつもりはない。もちろん、ここに書いたことがらはそのディテールにおいて新しさを主張するものではさらさらないが、しかし、私には自分が考えたことを他の誰かが先に考えていたかどうかなどどうでもいいことなので、出典も一切挙げない。
　ただ、私が自らの考えに対する刺戟の或る大きな部分をフレーゲのすばらしい著作と我が友バートランド・ラッセル氏の仕事に負っていることには触れておきたい。
　この仕事が何らかの価値をもつとすれば、それはふたつの点に在る。第一に、ここには考えが表明されているという点に。それがうまく表明されていればいるほど、この価値は大きくなるだろう。核心が突かれていればいるほど。――その可能性には程遠いままに留まっていることをいま私は自覚している。単に、その務めを果たすには力が足りなすぎるのだ。――もっとうまくやる者たちが現われるのを希う。
　一方、ここに報告されている考えの真理性は非のうちどころがなく決定的だと思われる。私は、だから、件の諸問題を本質的にはすっかり解いてしまったと考えている。そして、それについて私に思い違いがなければ、この仕事の価値は、第二に、それらの問題が解かれたことによって果たされたことがいかに少ないかを示している点に在る。

１９１８年　ヴィーンにて
L. W.

*　 　*　 　*　 　*　 　*　 　*　 　*

1	世界は成り立っていることがらの総てだ。
	〔原註：〕 各文の番号としての小数は、当の文の論理的重要度、私の叙述においてその文に置かれているアクセントを示唆する。文 n.1、n.2、n.3 等々は No. n の文への註であり、n.m1、n.m2 等々は No. n.m の文への註、以下同様。
1.1	世界は事実の総体だ。もののではない。
1.11	世界は当の諸事実によって、そしてそれらが事実の総てであることによって規定されている。
1.12	というのは、事実の総体は、成り立っていることがらにくわえて、成り立っていないことがらの総てを規定するからだ。
1.13	論理的空間内の全事実が世界だ。
1.2	世界は諸事実に分解する。
1.21	ひとつのことがらは、その他の総ては同じままに、あるいは成り立ちあるいは成り立たないことがあり得る。
2	成り立っていることがら、事実は諸事態の存立〔das Bestehen〕だ。
2.01	事態は諸対象（諸事物、諸々のもの）の結びつきだ。
2.011	ものにとって何らかの事態の成分になり得ることは本質的だ。
2.012	論理においては何も偶然的ではない。ひとつのものがひとつの事態に現われ得るならば、当の事態の可能性はそのものにおいて予め定められているはずなのだ。
2.0121	もっぱら単独で存立し得るものに、あとから何らかの状況が当てはまったならば、それはあたかも偶然のように見えることだろう。 どんなものでも、それが何らかの事態に現われ得るならば、そのことはとうにそのもののうちに在るはずだ。 （論理的なことがらはただ可能なだけではあり得ない。論理はあらゆる可能性を扱い、総ての可能性は論理の事実だ。） そもそも空間的対象を空間の外に、時間的対象を時間の外に考えることなどできないように、我々はどんな対象も他の諸対象との結びつきの可能性の外に考えることはできない。 ひとつの対象をひとつの事態の脈絡において考えることができるとき、私はそれを当の脈絡の可能性の外に考えることはできない。
2.0122	ものは、それが総ての可能な状況に現われ得る点では、自立的だが、この自立性の形式は、事態との関聯の一形式、非自立性の一形式だ。（言葉が、単独でと文の中でとで、ふたつの相異なる仕方で現われることは不可能だ。）
2.0123	ひとつの対象を知っているとき、私はさらにそれの諸事態における現われの可能性全部を知っている。 （そうした可能性は何れも当の対象の本性のうちに在るはずだ。） あとから新たな可能性が見出されることはあり得ない。
2.01231	或る対象を知るには、私はたしかにその外的属性を知る必要はない――しかし、その内的属性の総てを知る必要がある。
2.0124	総ての対象が齎されているならば、それとともに総ての可能な事態も齎されている。
2.013	あらゆるものは、謂わば可能な諸事態から成るひとつの空間の中に在る。私は、その空間を虚だと考えることはできるが、その空間を伴わないものを考えることはできない。
2.0131	空間的対象は無限の空間の中に在るはずだ。（空間点はアーギュメントの座〔eine Argumentstelle〕だ。） 視野の中のひとつの場所は、もちろん赤いとは限らないが、何らかの色はもっているはずだ。それは謂わば色空間を周りにもっているのだ。音は何らかの高さをもっているはずであり、触覚の対象は何らかの硬さを、以下同様。
2.014	対象全般は総ての状況の可能性を含んでいる。
2.0141	ひとつの対象の諸事態における現われの可能性が、当の対象の形式だ。
2.02	対象は単純だ。
2.0201	諸複合体についてのどんな言明も、当の諸複合体の全成分についてのひとつの言明およびそれらの複合体を完全に記述する諸文へと分析され得る。
2.021	全対象は世界の実体を成す。だから、対象は合成されてはあり得ない。
2.0211	世界が何の実体ももたなかったならば、或る文が意味〔Sinn〕をもつかどうかは、別の或る文が真であるかどうかに依存することだろう。
2.0212	その場合、世界の像なるものを（当否はともあれ）デザインするのは不可能だろう。
2.022	どんなに現実の世界とは異なって想像された世界も、何か――或る形式――を現実の世界と共有しているはずなのは明らかだ。
2.023	この不変の形式はまさに全対象から成る。
2.0231	世界の実体は、何らかの形式を規定し得るだけであり、マテリアルな属性などひとつも規定し得ない。マテリアルな属性全般は特定の諸文によって初めて表わされる――対象全般の配置によって初めて形成される――のだから。
2.0232	大雑把に言えば、対象全般は無色だ。
2.0233	同じ論理的形式をもつふたつの対象は――それらの外的諸属性を別にすれば――もっぱらそれらが相異なっていることによって区別されている。
2.02331	或るものが他の何ものももっていない諸属性をもっている場合、ひとはそのものを或る記述によって他のものの中から簡単に浮かび上がらせ指し示すことができる。一方、そうではなくて、それらのもつ属性全部が共通しているような幾つかのものが存在する場合には、そのうちのひとつを示すのはそもそも不可能だ。 というのは、ひとつのものが何によっても際立てられないならば、私はそれを際立たせることなどできないからだ。そんなことができたならば、それはまさに際立てられてあるのだから。
2.024	実体は成り立っていることがらとは独立して存立するものだ。
2.025	それは形式と内容だ。
2.0251	空間、時間、色（有色性）は対象全般の形式だ。
2.026	諸対象が存在する場合に限り、世界の不変の形式は存在し得る。
2.027	不変のものと存立しているものと対象はひとつのものだ。
2.0271	対象は不変のもの、存立しているものであり、配置は変化するもの、不安定なものだ。
2.0272	諸対象の配置は事態を形成する。
2.03	ひとつの事態において当の諸対象は鎖の環のように互いに組み合わさっている。
2.031	ひとつの事態において当の諸対象は一定の仕方で互いに係り合っている。
2.032	ひとつの事態において当の諸対象が関聯し合っているその仕方が、当の事態の構造だ。
2.033	構造の可能性が形式だ。
2.034	事実の構造は諸事態の構造から成る。
2.04	存立している事態の総体が世界だ。
2.05	存立している事態の総体は、また、どの事態が存立していないかを規定する。
2.06	現実は諸事態の存立および非存立だ。 （我々は、諸事態の存立をポジティヴな事実、非存立をネガティヴな事実とも言う。）
2.061	事態全般は互いに独立している。
2.062	或る事態の存立ないし非存立から、別の或る事態の存立ないし非存立が推論されることはあり得ない。
2.063	全現実が世界だ。
2.1	我々は諸々の事実の像〔Bilder〕を自らに齎す。
2.11	像は論理的空間内の状況、諸事態の存立および非存立を表象する。
2.12	像は現実の模型だ。
2.13	ひとつの像の諸要素は当の像において特定の諸対象に対応する。
2.131	ひとつの像の諸要素は当の像において特定の諸対象の代理をつとめる。
2.14	像はその諸要素が一定の仕方で互いに係り合っている点に依拠している。
2.141	像は事実だ。
2.15	ひとつの像の諸要素が一定の仕方で互いに係り合っていることは、特定の諸物がそのように互いに係り合っていることを表象している。 そうした像の諸要素の関聯を当の像の構造と呼び、その可能性を当の像の写しの形式〔Form der Abbildung〕と呼ぶ。
2.151	ひとつの写しの形式は、特定の諸物が、当の像の諸要素がそうであるのと同じように、互いに係り合う可能性だ。
2.1511	像はそうして現実に関聯づけられており、現実に達する。
2.1512	それはものさしのように現実に当てられている。
2.15121	その目盛線の最も外側の点だけが測られる対象に触れる。
2.1513	この見解に拠れば、だから、像にはそれを像にする写しの関係がさらに必要とされる。
2.1514	その写しの関係は、当の像の諸要素と特定の諸事物の対応づけ〔den Zuordnungen〕から成る。
2.1515	これらの対応づけは謂わば当の像の諸要素の触手であり、それらによって当の像は現実に触れる。
2.16	事実が像であるためには、当の写されるものと何かを共有する必要がある。
2.161	像と写されるものには、それによってそもそも一方が他方の像であり得るような、同一の何かが在るはずだ。
2.17	像が、それ流の仕方で――正誤はともあれ――現実を写し得るために、現実と共有する必要があるのは、その写しの形式だ。
2.171	像はそれと同じ形式をもつあらゆる現実を写し得る。 空間的な像は総ての空間的なものを、色彩的な像は総ての色彩的なものを等々。
2.172	像は、だが、その写しの形式を写すことはできない。像はそれを呈す。
2.173	像はそのモデルを外から表わす〔darstellt〕（像の観点がその表わしの形式〔Form der Darstellung〕だ）。だから、像はそのモデルをあるいは正しくあるいは誤って表わす。
2.174	像は、だが、その表わしの形式の外に立つことはできない。
2.18	あらゆる像が、その形式が何であれ、現実をそもそも――正誤はともあれ――写し得るために、現実と共有する必要があるのは、論理的形式、つまり現実の形式だ。
2.181	ひとつの像の写しの形式が論理的形式であるとき、当の像を論理的像と呼ぶ。
2.182	あらゆる像は論理的像でもある。（一方、総ての像が例えば空間的なものな訳ではない。）
2.19	論理的像は世界を写し得る。
2.2	像は当の写されたものと写しの論理的形式を共有している。
2.201	像は諸事態の存立および非存立の可能性を表わすことで、現実を写す。
2.202	像は論理的空間内の或る可能な状況を表わす。
2.203	像はそれが表わす状況の可能性を含んでいる。
2.21	像は現実に一致するかしないかだ。それは正しいか正しくないか、真であるか偽であるかだ。
2.22	像はそれが表わすものを、その真偽とは独立して、その写しの形式によって表わす。
2.221	像が表わすものはその意味だ。
2.222	像の真偽は、その意味と現実との一致ないし不一致に在る。
2.223	像が真であるか偽であるかを認識するためには、我々はそれを現実と比較する必要がある。
2.224	像だけからでは、それが真であるか偽であるかは認識され得ない。
2.225	アプリオリに真な像などというものは存在しない。
3	事実の論理的像は思考〔der Gedanke〕だ。
3.001	「或る事態が思惟可能である」とは、我々がその事態の像を自らに齎し得ることを意味する。
3.01	真な思考の総体は世界の像だ。
3.02	思考はそれが考えている当の状況の可能性を含む。思惟可能なことがらは可能でもある。
3.03	我々は非論理的なことは何も考えることができない。そんなことができたら非論理的に考えていることになるだろうから。
3.031	嘗てひとは言った。神は総てを創造し得るが、しかし、論理法則一般に反するものごとだけは創造し得ない、と。――我々は「非論理的」世界なるものについて、それがどんなふうなのかを述べることはできない、という訳だ。
3.032	ひとが言語において「論理に反していること」を表わし得ないのは、幾何学において空間の法則一般に矛盾する図形をその諸座標によって表わし得ないこと、言い換えれば、存在しない点の座標を特定し得ないことと同断だ。
3.0321	たしかに我々は物理法則一般に反する事態を空間的に表わすことはできるが、しかし、幾何学の法則一般に反する事態をそうすることはできない。
3.04	アプリオリに正しい思考というのは、その可能性がその真理性を伴うようなものだろう。
3.05	或る思考が真であることを我々がアプリオリに認識し得るのは、その思考そのものから（比較するもの無しに）その真理性を認識し得るとき、ただそのときだけだろう。
3.1	文において思考は感官的に知覚可能なように現われる。
3.11	我々は文の感官的に知覚可能な記号（音声記号なり文字記号なり等々）を可能な状況の射影として利用する。 その射影方式は当の文の意味を考えること〔das Denken des Satz-Sinnes〕だ。
3.12	それによって我々が思考を表現する記号を、私は文記号と呼ぶ。文は世界に対して射影的関係にある文記号だ。
3.13	文には、その射影に属すことがらの総てが属すが、当の射影されることがらは属さない。 だから、射影されることがらの可能性は当の文に属すが、射影されることがらそのものは属さない。 文には、だから、その意味は含まれてはいないが、それを表現する可能性は含まれている。 （「文の内容」とは有意味な〔sinnvollen〕文の内容のことだ。） 文には、その意味の形式が含まれているが、内容は含まれていない。
3.14	文記号は、その諸要素、諸単語がそこにおいて一定の仕方で互いに係り合っている点に依拠している。 文記号は事実だ。
3.141	文は単語の寄せ集めではない。――（音楽的主題が音の寄せ集めではないように。） 文は分節されている。
3.142	事実だけが何らかの意味を表現し得る。名称のどんなクラスにもそれは為し得ない。
3.143	文記号が事実であることは、筆記なり印刷なりの通常の表現形式によって覆い隠される。 というのは、例えば印刷された文においては、文記号は単語と本質的に異なっては見えないからだ。 （だから、フレーゲが文を合成的名称と呼ぶことも可能だった。）
3.1431	文記号の本質は、それが諸文字記号ではなく空間的諸対象（例えば、テーブル、椅子、本）から構成されているのを我々が想像するとき、顕著になる。 その場合、それらのものの相対的な空間的配置が当の文の意味を表現する。
3.1432	「複合的記号「aRb 」は a が b に対して関係 R にあることを述べている」という訳ではなくて、「a 」が「b 」に対して或る関係にあることが aRb ということを述べているのだ。
3.144	状況をひとは記述することはできる。名指すことはできない。 （名称は点に似ている。文は矢印に。それは意味〔Sinn〕をもつ）
3.2	文において思考はその諸対象に当の文記号の諸要素が対応するように表現され得る。
3.201	そうした要素を私は「単純記号」と呼び、当の文を「完全に分析された」文と呼ぶ。
3.202	文において適用された単純記号を名称と言う。
3.203	名称は当の対象を指す〔bedeutet〕。当の対象がその意義〔Bedeutung〕だ。（「A 」は「A 」と同一の記号だ。）
3.21	ひとつの文記号における諸単純記号の配置に、ひとつの状況における諸対象の配置が対応する。
3.22	名称は当の文において当の対象の代理をつとめる。
3.221	対象全般を私は名指すことができるだけだ。諸記号がそれらの代理をつとめる。私はそれらについて語ることができるだけだ。それらを言い表わすことはできない。文はものがどのようであるかを述べることができるだけだ。それが何であるかを述べることはできない。
3.23	単純記号全般の可能性の要請は、意味の確定性の要請だ。
3.24	複合体を主題とする文は、当の複合体の成分〔Bestandteil〕を主題とする文に対して内的関係にある。 複合体はもっぱらその記述によって齎され得るが、そうした記述はあるいは適切でありあるいは適切でないだろう。それにおいて或る複合体が話題にされている文は、当の複合体が存在しない場合、ナンセンス〔unsinnig〕ではなくて、単に偽だろう。 或る文要素〔ein Satzelement〕が何らかの複合体を表示することを、ひとは、それが現われる文全般における或る不定性から見て取ることができる。総てが当の文によって特定されている訳ではないことを、我々は諒解する。（一般性表示〔Die Allgemeinheitsbezeichnung〕は何らかのプロトタイプ〔ein Urbild〕を含むのだ。） ひとつの複合体のシンボルの単純なシンボルへの要約は何らかの定義でもって表現され得る。
3.25	ひとつの文の完全な分析はただひとつだけ存在する。
3.251	文は、それが表現することがらを、或る種の明確に特定可能な仕方で表現する。文は分節されているのだ。
3.26	名称が定義でもってさらに解体されることはあり得ない。つまり、名称は原記号だ。
3.261	どんな定義された記号も、その定義に用いられた諸記号を経由して表示する〔bezeichnet〕。そして、当の定義がその道を指し示す。 一方は原記号で他方は諸原記号によって定義された記号であるような、そんなふたつの記号が同じ仕方で表示することはあり得ない。名称をひとは定義でもって展開することはできない。（単独で自立的に意義をもつ記号など無い。）
3.262	記号において現われないものを、当の記号の適用が示す。記号が内に湛えているものを、当の記号の適用が顕わにする。
3.263	原記号の意義は註解によって説明され得る。そうした註解は当の原記号を含む文だ。それは、だから、当の記号の意義が既に知られているならば、とにかく理解されることはされ得る。
3.3	文だけが意味をもち、文のコンテクストにおいてだけ名称というものは意義をもつ。
3.31	ひとつの文の意味を特徴づけるような当の文のあらゆる部分を私は表現（シンボル）と呼ぶ。 （当の文そのものも表現だ。） ひとつの文の意味にとって本質的なもの、諸文が互いに共有し得るものの総てが表現だ。 表現は或る形式と内容をマークする。
3.311	ひとつの表現は、それが現われ得る総ての文の形式を前提としている。それは文の或るクラスの共通の特徴的メルクマールだ。
3.312	ひとつの表現は、だから、それが特徴づける文全般がもつ一般的形式によって表わされる。 しかも、この形式においては、その表現は固定的であり、他の総ては可変的だろう。
3.313	ひとつの表現は、だから、その値が何れも当の表現を含む文であるような或る変数によって表わされる。 （境界ケースでは、変数は定数に、表現は文になる。） 私はそうした変数を「文変数」と呼ぶ。
3.314	表現はただ文においてだけ意義をもつ。どんな変数も文変数と解され得る。 （変数的名称もまた。）
3.315	我々が或る文の或る成分〔einen Bestandteil〕を変数に替えれば、それによって生じた変数的文の値であるような文全部から成るクラスが齎される。このクラスは、一般に、我々が恣意的な合意によってもとの文の諸部分〔Teilen〕で何を指し示すのかに依存するが、しかし、その意義が恣意的に決められた記号の総てを変数に替えても、やはりそうしたクラスは齎される。これは、だが、もうどんな合意にも依存せず、ただ件の文の本性にだけ依存する。それは或る論理的形式――或る論理的プロトタイプ――に対応する。
3.316	ひとつの文変数がどんな値をとることが許されるかは、約定される。 その値全般の約定が当の変数だ。
3.317	ひとつの文変数の値全般の約定は、当の変数を共通のメルクマールにもつような文全般の陳述だ。 それらの文の記述が当の約定だ。 その約定は、だから、諸シンボルだけを扱い、それらの意義〔Bedeutung〕は扱わないだろう。 そして、その約定においては、それが諸シンボルの記述に過ぎず、それらによって表示されるものについては何ごとも言明しはしないこと、ただそれだけが本質的だ。 当の諸文の記述がどう為されるかは非本質的だ。
3.318	文を私は――ラッセルおよびフレーゲと同じく――それに含まれる諸表現の関数と解する。
3.32	記号はシンボルの感官的に知覚可能な部分だ。
3.321	ふたつの相異なるシンボルは、だから、ひとつの記号（文字記号なり音声記号なり等々）を共有し得る――その場合、それらは相異なる仕方で表示する。
3.322	我々がふたつの対象を同一の記号によって、しかしふたつの相異なる表示方法で表示することが、それらに共通するメルクマールを呈示することなど決してあり得ない。当の記号は恣意的なのだから。ひとは、だから、ふたつの相異なる記号を採ることもできただろうが、その場合、当の表示の何処に共通のものが残るだろうか。
3.323	日常言語においては、同一の語が色々な仕方で表示する――故に色々なシンボルに属す――こと、あるいは、相異なる仕方で表示するふたつの語が表面上同じ仕方でひとつの文において適用されることが非常に頻繁に起る。 例えば、「ist」〔ドイツ語の動詞「sein」の三人称単数現在形〕は繋辞としても等号としても存在の表現としても現われる。「existieren」〔「存在する」〕は「gehen」〔「行く」〕と同様の自動詞として、「identisch」〔「同一の」〕は形容詞として。我々は何か〔Etwas 〕について話すが、何か〔etwas 〕が起ることについても話す。 （文「Grün ist grün」――ただし、最初の語は人名で最後の語は形容詞〔そこで日本語で同様の例を考えてみれば「あおいはあおい」〕――において、これらの語は単に相異なる意義をもつのではない。それらは相異なるシンボルだ。）
3.324	それで、最も根本的な諸混同がたやすく生じる（哲学全体がそれらに充ちている）。
3.325	それらの錯誤を免れるために、我々は、同一の記号を色々なシンボルにおいて用いたり相異なる仕方で表示する諸記号を表面上同じ仕方で用いたりしない点で、そうした錯誤を排除するような、そんな何らかの記号言語を利用する必要がある。したがって、論理的文法――論理的構文論――に則る記号言語を。 （フレーゲの、そしてラッセルの概念記法は、そうした言語のひとつではあるものの、総ての誤謬を排除している訳ではない。）
3.326	記号にシンボルを認識するには、ひとは当の記号の有意味な使用に注意を払う必要がある。
3.327	記号は、その論理的構文論的利用と相俟って初めて、何らかの論理的形式を規定する。
3.328	或る記号が不用ならば、それは無意義〔bedeutungslos〕だ。これがオッカムの標語の意味だ。 （或る記号が意義をもつかのように総てがなっているならば、それは実際に意義をもつ。）
3.33	論理的構文論においては、記号の意義が何らかの役割を果たすことは決して許されない。論理的構文論は、記号の意義が話題にされることなど無しに、組み立てられ得るのでなければならない。それが前提とすることが許されるのは、ただその諸表現の記述だけだ。
3.331	この所見をもとにラッセルの「タイプ理論」に目を向けよう。ラッセルの錯誤は、その記号規則全般を立てる際に当の諸記号の意義について語るはめになった点に自ずと顕現する。
3.332	文が自らについて何ごとかを言明することなどあり得ない。文記号がそれ自体に含まれることはあり得ないから。（これが全「タイプ理論」だ。）
3.333	どんな関数も自らのアーギュメント〔いわゆる引き数〕ではあり得ない。関数記号はそのアーギュメントのプロトタイプをもう含んでいるのであり、自らを含むことはあり得ないから。 仮に関数 F (fx ) が自らのアーギュメントであり得たとしよう。そうすると「F (F (fx ))」という文が齎されるが、この文において、外側の関数 F と内側の関数 F は相異なる意義をもっているはずだ。内側の方は φ(fx ) という形式を、外側の方は ψ(φ(fx )) という形式をもっているのだから。両方の関数に共通するのは文字「F 」だけだが、しかし、それは単独では何も表示しはしない。 このことは、「F (F (u ))」に代えて「(∃φ ) : F (φu ) . φu = Fu 」と書けばただちに明らかになる。 これでラッセルのパラドクスは片がつく。
3.334	論理的構文論の規則全般は、ひとがそれぞれの記号が如何に表示するのかを諒解してさえいれば、自明なはずだ。
3.34	文は本質的な諸相と偶然的な諸相をもっている。 偶然的なのは、その文記号を齎す特殊な仕方に由来する諸相だ。本質的なのは、それらだけで当の文にその意味を表現することを可能にする諸相だ。
3.341	ひとつの文の本質を成すのは、だから、それと同じ意味を表現し得る総ての文に共通するものだ。 同様に、ひとつのシンボルの本質を成すのは、一般に、それと同一の目的を果たし得る総てのシンボルが共有するものだ。
3.3411	ひとは、だから、こう言い得るだろう： 本来の名称は、同一の対象を表示する総てのシンボルが共有するものだ。名称にとってはどんな構成も全く本質的ではないことが、これでサクセッシヴに〔succesive〕明らかになることだろう。
3.342	我々の表記法にはたしかに恣意的なところが在るが、しかし、これは恣意的ではない： 我々が何ごとかを恣意的に定めおおしたときには、何か別のことがらが必然的に成り立っている。（このことは当の表記法の本質に依存する。）
3.3421	或る特殊な表示方法は重要ではないかも知れないが、それがひとつの可能な表示方法であることは恒に重要だ。それに、そもそも哲学においてはこうなっている： 個々のことがらが重要でないことは繰り返し明らかになるが、それぞれのことがらの可能性は我々に世界の本質についての何らかの情報を齎す。
3.343	ひとつの言語から別の言語への翻訳のための或る種の規則は、定義だ。あらゆるまっとうな記号言語は、そうした規則に随って、他のどんなまっとうな記号言語にも翻訳され得るはずだ。そして、これがそれらの総てが共有することがらだ。
3.344	ひとつのシンボルにおいて表示するのは、論理的構文論の規則全般に則って当のシンボルに置き換えられ得るような総てのシンボルに共通する部分だ。
3.3441	ひとは、例えば、真理関数のための表記法の総てに共通することがらをこう表現することができる： それらに共通するのは、総てが――例えば――「〜p 」（「非 p 」）および「p ∨ q 」（「p または q 」）という表記法で置き換えられ得ることだ。 （これには、ひとつの特殊な可能的表記法がどうして我々に一般的諸情報を齎し得るかがマークされている。）
3.3442	複合体の記号は、その分析の際にも、例えばそのそれぞれの文構造における分解がいちいち異なるなどというように、恣意的に分解されたりはしない。
3.4	文は論理的空間内の或る軌跡を規定する。この論理的軌跡の存在は、もっぱらその諸成分の存在によって保証される。当の有意味な文の存在によって。
3.41	ひとつの文記号と一連の論理的座標、それがひとつの論理的軌跡だ。
3.411	幾何学的軌跡と論理的軌跡は、どちらも何らかの存在の可能性である点で一致する。
3.42	ひとつの文は論理的空間のただひとつの軌跡を規定し得るだけではあるものの、当の文によって論理的空間全体が既に齎されているはずだ。 （そうでなければ、否定、論理和、論理積等々によって、絶えず新たな要素が――座標系に〔in Koordination〕――導入されることになるだろう。） （像を囲む論理的な足場が論理的空間を規定する。文は論理的空間全体に手を伸ばす。）
3.5	適用された、考えられた文記号は思考だ。
4	思考は有意味な文だ。
4.001	文の総体が言語だ。
4.002	人間は、それぞれの単語が何をどう指すのかについての漠然とした知識も無しに、諸々の言葉を組み立てる能力をもっており、それであらゆる意味が表現され得る。――ひとは、また、個々の音声がどうやって発されるのかを理解すること無く喋る。 日常言語は、人間という有機体の一部であり、それに劣らず複雑だ。 ひとつの言語論理〔die Sprachlogik〕を日常言語から直接取り出すことは人間には叶わない。 言語は思考を扮装させる。しかも、ひとが当のドレスの外形に拠っては覆われている思考の形を推論し得ないほどに。それは、そのドレスの外形が中身の形を認識させるためとは全く違う目的に随って形成されているからだ。 日常言語の理解のための暗黙の協定全体は度外れに複雑だ。
4.003	諸々の哲学的なものごとについて書かれて来た教義や問いの大部分は、誤りではなく、ナンセンスだ。我々は、だから、その種の問いにそもそも答えることなどできず、ただそれらのナンセンス性を確かめることができるだけだ。哲学者たちの問いと教義の大部分は、我々が自分たちの言語論理を理解していないことに基く。 （それらは、善は美と多少なりとも一致するか、といった類の問いだ。） そして、最も深遠な諸問題が実は何の問題でもない、というのは驚くべきことではない。
4.0031	総ての哲学は「言語批判」だ。（ただし、マウトナーの意味でではない。）ラッセルの功績は、文の見かけの論理的形式が当の文の実際の形式だとは限らないことを示したことだ。
4.01	文は現実の像だ。 文は現実の模型であり、我々は現実をそのように思い浮かべる。
4.011	ひとつの文――例えば紙に印刷されてあるような――は一見それが主題とする現実の像らしくなどない。だが、楽譜もまた一見音楽の像らしくなどないし、我々の音声記号（アルファベット）表記も音声言語の像らしくなどない。 それでもやはり、そうした記号言語は何れも、ごく普通の意味においても、それが表わすものの像であることが明らかになる。
4.012	我々が「aRb 」という形式の文を像として感じていることは明らかだ。ここで、記号は明らかにそれによって表示されるものごとの喩〔ein Gleichnis〕だ。
4.013	そして、我々がこの像性〔Bildhaftigkeit〕の本質を成すものに通じるならば、同じ像性は（楽譜における♯と♭の利用のような）諸々の見かけの不規則性によって損なわれはしないことが判る。 というのは、そうした不規則性もまたそれらが表現すべきことがらを写すからだ。ただし、或る別の仕方で。
4.014	ひとつの音盤とその音楽的思考とその楽譜とその音波の総ては、互いに、言語と世界の間に存立する例の写しの内的関係にある。 それらの総てに共通しているのが論理的構造だ。 （あの昔話の二人の若者と彼らの二頭の馬と彼らの二株の百合のように。それらは或る意味で総てひとつのものだ。）
4.0141	それによって音楽家がひとつのスコアから当の交響曲を察知することができるような或る一般的規則が存在して、それによってひとがひとつの音盤の溝からその交響曲を、そして最初の規則に随ってまた当のスコアを抽き出すことができること、まさにこの点に、それらの見かけは全く相異なる構造体の内的相似性が在る。そして、件の規則は交響曲を楽譜言語に射影する射影法則だ。それは楽譜言語から音盤言語への翻訳規則だ。
4.015	総ての喩の可能性、我々の表現方法の像性全体の可能性は、写しの論理のうちに憩っている。
4.016	文の本質を理解するために、ヒエログリフ表記を考えよう。この表記は、それが記述する事実を写す。 そして、それから、写しの本質を成すものを失うこと無く、アルファベット表記が生じた。
4.02	そのことは、我々が文記号の意味を、それが説明されたことが無くても、理解することから判る。
4.021	文は現実の像だ。文を理解するとき、私はそれによって表わされている状況を知るのだから。そして、私は当の文を、その意味が説明されたことが無くても、理解する。
4.022	文はその意味を示す。 文は、それが真なときには〔現実は〕どうなっているのか、を示す。そして、そうなっていることを述べる。
4.023	現実は文によって肯定か否定で捉えられているはずだ。 そのためには、現実は当の文によって完全に記述される必要がある。 文は何らかの事態の記述だ。 対象の記述が当の対象をその外的諸属性に随って記述するように、文は現実をその内的諸属性に随って記述する。 文は或る論理的な足場の援けによって何らかの世界を構成する。だから、ひとは文に、それが真なときには論理的なことがらの総てはどうなっているのか、を見て取ることもできる。ひとは偽な文から諸結論を引き出すことができる。
4.024	ひとつの文を理解するとは、それが真なときには何が成り立っているのか、を把握することを意味する。 （ひとは、だから、その文を、それが真であるかどうかを把握すること無く、理解することができる。） その諸成分を理解するとき、ひとは当の文を理解する。
4.025	或る言語の別の或る言語への翻訳は、ひとが一方の個々の文を他方の文に翻訳するというように為されるのではなくて、ただ文の諸成分だけが翻訳される。 （そして、辞書は、名詞だけでなく、動詞や形容詞や接続詞等々も翻訳するのであり、それらを総て同様に扱う。）
4.026	単純記号全般（単語全般）の意義〔die Bedeutungen〕は、我々がそれらを理解するためには、説明される必要がある。 一方、文全般によって我々はコミュニケートする。
4.027	文が我々に新たな意味を伝え得ることは、当の文の本質のうちに在る。
4.03	文というものは諸々の古い表現によって新たな意味を伝えざるを得ない。 ひとつの文は我々に何らかの状況を伝える。だから、それは当の状況と本質的に関聯しているはずだ。 そして、それが当の状況の像であることこそが、その関聯だ。 文は、ただそれが像である限りにおいて、何ごとかを言明する。
4.031	ひとつの文においては、何らかの状況が謂わばサンプルとして構成される。 ひとは、この文はしかじかの意味をもつと言う替わりに、この文はしかじかの状況を表わしていると直截に言うことができる。
4.0311	或る名称は或るものを、別の或る名称は別の或るものを代表し、互いに結びつけられており、そうしてそれらの全体がひとつの状況を――活人画のように――表象する。
4.0312	文の可能性は、記号による対象の代理の原理に基いている。 私の根本的な考えは、「論理定数」なるものは代理をつとめないということ、事実全般の論理は代理され得ないということだ。
4.032	文は、もっぱらそれが論理的に組み立てられている点において、何らかの状況の像だ。 （「Ambulo」〔「私は歩き廻る」というほどの意味のラテン語の一語文〕という文さえ合成されている。その語幹は他の語尾とともに、そして、その語尾は他の語幹とともに、別々の意味を齎すのだから。）
4.04	文にはそれが表わす状況にとちょうど同じだけの区別がつけられ得るはずだ。 それらは両方とも同じ論理的（数学的）多様性をもっているはずだ。（動力学的諸模型については、ヘルツの力学を参照せよ。）
4.041	ひとは、もちろん、この数学的多様性そのものをさらに写すことはできない。写しの際にこの多様性の外に出ることはできない。
4.0411	我々が、例えば、「(x ) . fx 」によって表現していることがらを、「fx 」の前にインデクスを附けることで――例えば「Alg . fx 」というように――表現しようとしても、うまくいかないだろう――我々は何が一般化されているのか判らないだろう。それをインデクス「a 」によって――例えば「fxa 」というように――呈示しようとしても、うまくいかないだろう――我々は一般性表示の範囲が判らないだろう。 それをアーギュメントの座にマークを導入することによって――例えば 「(A, A ) . F (A, A )」 というようにして――どうにかしようとしても、うまくいかないだろう――我々は変数の同一性を確かめることができないだろう。以下同様。 これらの表示方法は何れも、必要な数学的多様性をもっていないため、十分ではない。
4.0412	同じ理由から、「空間眼鏡」による空間的関係全般の観取という観念論的説明は十分ではない。それは当の諸関係の多様性を説明し得ないのだから。
4.05	現実は文と比較される。
4.06	文は、もっぱらそれが現実の像であることによって、真ないし偽であり得る。
4.061	文が事実全般とは独立した意味をもつことに注意を払わないとき、ひとは、真と偽はどちらも記号とそれによって表示されるものとの関係であり同権だと考えやすい。 それで、ひとは、例えば、「p 」は「〜p 」が偽な仕方で表示することがらを真な仕方で表示する等々と言うかも知れない。
4.062	ひとは、これまで真な諸文によってしてきたのと同様に、偽な諸文によってコミュニケートし得るのではないか？ それらが偽だと考えられていることを諒解している限りは。いいや！ だって、或る文が真なのは、我々がその文によって述べるとおりに〔現実が〕なっている場合なのであり、我々が「p 」によって 〜p と考え、しかも我々が考えるとおりになっているならば、「p 」はこの新たな解釈において真であって、偽ではないのだから。
4.0621	一方、「p 」と「〜p 」がおなじことを述べ得ることは重要だ。それは記号「〜」には現実における何ごとも対応しないことを示しているのだから。 或る文に否定が現われることは、当の文の意味のメルクマールなどではないのだ（〜〜p = p ）。 文「p 」と「〜p 」は反対の意味をもつが、それらには同一の現実が対応する。
4.063	真理概念の説明のためのひとつの挿画： 白い紙の上の黒い染み。ひとはその染みの形を、当の紙面の各点についてそれが白いか黒いかを特定することによって、記述し得る。或る点が黒いという事実には或るポジティヴな事実が対応する――或る点が白い（黒くない）という事実には或るネガティヴな事実が。私がその表面の或る点（フレーゲ流の真理値）を指し示すとき、そのことにはひとつの判断のために立てられる仮定が対応する等々。 だが、ひとつの点を黒いとか白いとか言い得るためには、私は、とりあえず、ひとがひとつの点をどんな場合に黒いと言い、どんな場合に白いと言うのかを諒解している必要がある。「p 」は真だ（あるいは偽だ）と言い得るためには、どんなシチュエーションにおいて「p 」を真だと言うのかを決めておく必要があり、それによって私は当の文の意味を規定する。 この比喩のまずい点はともあれこれだ： 我々は、何が白くて何が黒いのか解らなくとも、件の紙面の点を示すことができるが、しかし、意味を伴わない文には全く何も対応しない。それは「真」だとか「偽」だとかと言われるような属性をもつもの（真理値）など何も表示しはしないのだから。「真である」も「偽である」も文の動詞ではない――フレーゲはそうだと考えた訳だが。そうではなくて、「真である」ものは当の動詞をもう含んでいるはずだ。
4.064	どんな文もとうに何らかの意味をもっているはずだ。肯定が当の文にその意味を齎すことはあり得ない。肯定はまさに当の意味を肯定するのだから。そして、同様のことが否定等々に当てはまる。
4.0641	ひとはこう言い得るだろう： 否定は否定される文が規定する論理的軌跡にとうに関わっている。 ひとつの否定文は否定された文が規定するのとは別の或る論理的軌跡を規定する。 ひとつの否定文は或る論理的軌跡を否定された文の論理的軌跡の援けによって規定する。その軌跡を否定された文の軌跡の外に在るものとして記述することによって。 ひとが否定された文をふたたび否定し得ることは、否定されるものはもう何らかの文であり、文への前段階にあるものなどではないことをまさに示している。
4.1	ひとつの文は特定の諸事態の存立および非存立を表わす。
4.11	真な文の総体が全自然科学（あるいは種々の自然科学の総体）だ。
4.111	哲学は自然科学の一種ではない。 （「哲学」という語は、種々の自然科学に並ぶ何かではなく、それらより上か下かに位置するものを指すはずだ。）
4.112	哲学の目的は思考全般の論理的浄化だ。 哲学は教えではなく、活動だ。 哲学の作品というものは本質的に諸註解から成る。 哲学の結果は「哲学的教義」などではなくて、諸教義の明晰化だ。 哲学はそのままでは謂わば濁っていて曖昧な思考全般を明晰にし、はっきりと限定すべきだ。
4.1121	心理学が、何か他の自然科学よりも、哲学に類似しているなどということはない。 認識論は心理学の哲学だ。 私の記号言語研究は、哲学者たちが論理の哲学にとってあれだけ本質的だと考えた思惟プロセスの研究に相当するのではないか？ 彼らは大抵ただ非本質的な心理学的諸探究に巻き込まれただけだったが、似たような危険が私のやり方にも存在する。
4.1122	ダーウィン理論が、何か他の自然科学の仮説よりも、哲学に関わりがあるなどということはない。
4.113	哲学は自然科学が反論可能な領域を限定する。
4.114	哲学は思惟可能な領域を劃定し、そして、それによって思惟不能な領域を劃定すべきだ。 哲学は、思惟可能な領域の内側から、思惟不能な領域を限定すべきだ。
4.115	哲学は、所述可能なことがらを明確に表わすことで、所述不能なことがらを暗示するだろう。
4.116	そもそも考えられ得ることがらの総ては明確に考えられ得る。言い表わされ得ることがらの総ては明確に言い表わされ得る。
4.12	文は全現実を表わし得る。しかし、文は、それが現実を表わし得るためには当の現実と共有する必要があるもの――論理的形式――を表わすことはできない。 当の論理的形式を表わし得るためには、我々はその文とともに論理の外に立ち得るのでなければならないだろう。つまり、世界の外に。
4.121	文は当の論理的形式を表わし得ない。それは当の文に反映する。 言語に反映するものを、言語は表わし得ない。 言語において自ずと現われるものを、我々が言語によって表現することはできない。 文は現実の論理的形式を示す。 文はそれを呈す。
4.1211	例えば、「fa 」という文は、その意味の中に対象 a が現われることを示しており、「fa 」と「ga 」というふたつの文は、両方で同じ対象が話題にされていることを示している。 ふたつの文が互いに矛盾する場合、そのことはそれらが成す構造を示しており、一方が他方から帰結する場合も同様だ。以下同様。
4.1212	示され得ることがらは述べられ得ない。
4.1213	我々の記号言語においてひとたび総てが調和しさえすれば、我々は正しい論理的見解をもつのだ、という自分たちの感じも、いま我々には解る。
4.122	我々は、或る意味で、対象と事態の形式的属性について、あるいは事実の構造の属性について語ることができる。また、それと同じ意味で、形式的関係および諸構造の関係についても。 （構造の属性に替えて私は「内的属性」とも言い、諸構造の関係に替えて「内的関係」とも言う。 私は、これらの表現を、哲学者たちのもとでやたらに蔓延させられている内的関係一般と本来の（外的）関係一般との混同の由来を示すために導入する。） だが、そうした内的な属性や関係の存立は何れも文によっては主張され得ず、当の事態を表わす文や当の対象を主題とする文において自ずと顕現する。
4.1221	ひとつの事実の内的属性を我々は当の事実の相とも呼ぶ。（我々が例えば相貌について語るその意味において。）
4.123	ひとつの属性が内的なのは、当の対象がそれをもたないことが思惟不能な場合だ。 （この青色とあの青色は、それら自体で〔eo ipso〕、より明るいおよびより暗いという内的関係にある。これらふたつの対象がこの関係にないことは思惟不能だ。） （ここで、「属性」および「関係」という語の揺動する使用に「対象」という語の揺動する使用が対応している。）
4.124	ひとつの可能な状況の内的属性の存立は、どんな文によっても表現されず、当の属性を表わす文において、その文の或る内的属性を通じて自ずと現われる。 文に何らかの形式的属性を認めることは、それを否認することと同じくナンセンスだろう。
4.1241	諸形式を、ひとは、一方はこの属性をもつが他方はあの属性をもつ、と述べることで区別することはできない。それは両方の形式について両方の属性を言明することが意味をもつことを前提としているから。
4.125	可能な諸状況の間の何らかの内的関係の存立は、それらを表わす諸文の間の或る内的関係を通じて言語的に自ずと現われる。
4.1251	ここで、「総ての関係は内的なのか外的なのか」という論争の的となっている問題は片がつく。
4.1252	或る種の内的関係によって順序づけられている列を私は形式列と呼ぶ。数列というものは、外的関係に随ってではなく、何らかの内的関係に随って順序づけられている。 文の列 「aRb 」、 「(∃x ) : aRx . xRb 」、 「(∃x, y ) : aRx . xRy . yRb 」、 以下同様 についても同様だ。（b が a に対してこれらの関係のうちのひとつにあるとき、私は b を a の後継と呼ぶ。）
4.126	我々は、形式的諸属性について語るその意味で、さらに、形式的諸概念について語ることができる。 （私は、この表現を、旧い論理学全体を貫いている形式的概念一般と本来の概念一般との混同の由来を明らかにするために導入する。） 何かが或る形式的概念のもとにその対象として収まることは、どんな文によっても表現され得ず、当の対象の記号そのものに自ずと顕現する。（ひとつの名称はそれが或る対象を表示することを示し、ひとつの数字はそれが或る数を表示することを等々。） 形式的概念は、本来の概念とは違って、どんな関数によっても表わされ得ないのだ。 そのメルクマール、形式的属性はどんな関数によっても表現されないのだから。 形式的概念の表現は或る種のシンボルの相だ。 ひとつの形式的概念のメルクマールの記号は、だから、その意義が当の概念のもとに収まるようなシンボルの総てがもつひとつの特徴的相だ。 当の形式的概念の表現は、だから、そこにおいてただ当の特徴的相だけが定数であるような文変数だ。
4.127	文変数は形式的概念を表示し、その値は何れも当の概念のもとに収まる対象を表示する。
4.1271	どんな変数も何らかの形式的概念の記号だ。 というのは、どんな変数もその値の総てがもつ或る不変の形式を表わしており、その形式はそれらの値の形式的属性と解され得るからだ。
4.1272	そんな訳で、変数的名称「x 」は対象という見かけの概念の本来の記号だ。 「対象」（「もの」、「事物」等々）という語が適切に使われるとき、それは概念記法において変数的名称によって表わされる。 例えば「・ ・ ・ のような 2 箇の対象が存在する」という文では「(∃x, y ) ・ ・ ・」によって。 一方、それが本来の概念語として使われるときには、諸々のナンセンスな、見かけの文が生じる。 ひとは、例えば、「諸々の本が存在する」などと言うのと同じように「諸対象が存在する」と言うことはできない。「100 箇の対象が存在する」とか「0 箇の対象が存在する」についても同断だ。 また、総ての対象の箇数について語るのもナンセンスだ。 同様のことが、「複合体」、「事実」、「関数」、「数」等々の語についても当てはまる。 それらは何れも或る形式的概念を表示しており、概念記法においては、（フレーゲとラッセルが考えたように）関数やクラスによってではなく、何らかの変数によって表わされる。 「1 は数である」とか「ただひとつのゼロが存在する」といった表現や総ての似たような表現はナンセンスだ。 （「2 + 2 は 3 時には 4 に等しい」と言うことはナンセンスだろうが、「ただひとつの 1 が存在する」と言うことも同様にナンセンスだ。）
4.12721	形式的概念はもうそのもとに収まる或る対象とともに齎されている。ひとは、だから、或る形式的概念の諸対象および当の形式的概念そのものを根本的概念として導入することはできない。ひとは、だから、例えば関数という概念およびそれに加えて特殊な関数を（ラッセルのように）根本的概念として導入することはできない。あるいは、数という概念と或る種の数を。
4.1273	「b は a の後継である」という一般的文を概念記法において表現したければ、我々はそのために次のような形式列の一般項のための表現を必要とする。 aRb, (∃x ) : aRx . xRb, (∃x, y ) : aRx . xRy . yRb, . . . 形式列の一般項をひとはただ何らかの変数によってだけ表現することができる。この形式列の項、という概念は形式的概念なのだ。（このことをフレーゲとラッセルは見落としている。彼らが上のような一般的文を表現するものとする方法は、だから、誤りだ。それは悪循環〔circulus vitiosus〕を含んでいる。） 我々は形式列の一般項を、その第一項を挙げ、そして先行する文から後続項を齎すオペレーションの一般的形式を挙げることによって、規定することができる。
4.1274	形式的概念の存在についての問いはナンセンスだ。そのような問いに答え得る文など無いのだから。 （ひとは、だから、例えば「分析不能な主語述語文は存在するか？」と問うことはできない。）
4.128	論理的形式全般は無数〔zahllos 〕だ。 だから、論理には特別な数など存在しないし、だから、哲学的一元論や二元論等々は存在しない。
4.2	ひとつの文の意味は、当の文と特定の諸事態の存立および非存立の可能性との一致および不一致だ。
4.21	最も単純な文、基本的文〔der Elementarsatz〕は何らかの事態の存立を主張する。
4.211	基本的文のひとつの徴は、どんな基本的文もそれと矛盾し得ないことだ。
4.22	基本的文は諸名称から成る。それは諸名称の聯関、連鎖だ。
4.221	我々は、どんな文の分析に際しても、直接に結びつきあった諸名称から成る諸基本的文に到るはずであること、これは明らかだ。 ここで、文の脈絡〔der Satzverband〕が如何に実現するかが問題になる。
4.2211	たとえ世界が、あらゆる事実は無限に多くの事態から成り、あらゆる事態は無限に多くの対象から構成されている、というように無限に複雑であっても、それでもやはり諸対象と諸事態は存在するに違いないだろう。
4.23	名称は、ただ基本的文のコンテクストにおいてだけ、文に現われる。
4.24	名称全般は単純なシンボルだ。私はそれらを個々の文字（「x 」、「y 」、「z 」）によって示唆する。 基本的文を、私は、諸名称の関数として、「fx 」、「φ(x, y )」等々の形式で書く。 あるいは、私はそれらを文字 p 、q 、r によって示唆する。
4.241	ふたつの記号を同一の意義で使うとき、私はそのことをそれらの間に記号「=」を置いて表現する。 「a = b 」は、だから、記号「a 」は記号「b 」で置換可能なことを意味する。 （新たな記号「b 」を等式を通じて導入し、それが既に知られている記号「a 」の代わりになるものと定める場合、私はその等式――定義――を（ラッセルのように）「a = b　Def.」という形式で書く。定義は記号規則だ。）
4.242	「a = b 」という形式の表現は、だから、叙述の便法に過ぎず、記号「a 」、「b 」の意義については何ごとも言明しはしない。
4.243	我々は、ふたつの名称を、それらが同一のものを表示するのかそれともふたつの別々のものを表示するのかを把握すること無く、理解することができるか？ ――我々は、そこにおいてふたつの名称が現われる或る文を、それらの名称が同一のものを指すのかそれとも別々のものを指すのかを把握すること無く、理解することができるか？ 私が、例えば、或る英単語の意義およびそれと同義のドイツ語の単語の意義を知っているとき、それらふたつの語が同義であることを把握していないなどということはあり得ない。それらを互いに置き換え得ないなどということはあり得ない。 「a = a 」のような諸表現やそれらから派生する諸表現は、基本的文でもなければ有意味な記号ですらない。（このことはのちに明らかになる。）
4.25	ひとつの基本的文が真なとき、当の事態が存立しており、ひとつの基本的文が偽なとき、当の事態は存立していない。
4.26	総ての真な基本的文の陳述は、世界を完全に記述する。世界は、総ての基本的文の陳述プラスそれらのうちのどれが真でありどれが偽であるかの陳述によって、完全に記述されている。
4.27	n 箇の事態の存立と非存立に関しては 箇の可能性が在る。 それらの事態のあらゆるコンビネーションが存立し得るが、ひとつが存立すればその他は存立しない。
4.28	これらのコンビネーションには、n 箇の基本的文の真偽の可能性がちょうど一対一に対応する。
4.3	基本的文の真理可能性とは、当の事態の存立ないし非存立の可能性のことだ。
4.31	特定の諸真理可能性を我々は次のような類の図式によって表わすことができる（「W」は「真〔wahr〕」を、「F」は「偽〔falsch〕」を指す。基本的文の列の下の「W」と「F」から成る各列はそれらの文の真理可能性を判り易いシンボリックで示唆している）。
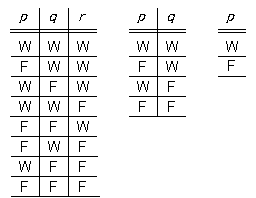4.4	ひとつの文は、特定の諸基本的文の全真理可能性との一致および不一致の表現だ。
4.41	当の諸基本的文の真理可能性のそれぞれがその文の真偽の条件だ。
4.411	基本的文全般の導入が他の総ての種類の文の理解のための基礎を成すことはもとより見当がつく。一般的文全般の理解は基本的文全般の理解に著しく依存するのだ。
4.42	ひとつの文と n 箇の基本的文の全真理可能性との一致および不一致に関しては 箇の可能性が在る。
4.43	特定の諸真理可能性との一致を、我々は、それらに件の図式において例えば符号「W」（真）を対応づけることによって、表現することができる。 この符号を欠いていることは、不一致を暗示する。
4.431	当の諸基本的文の全真理可能性との一致および不一致の表現は、当の文の諸真理条件を表現する。 文はその諸真理条件の表現だ。 （フレーゲは、だから、適切にも、それらを彼の概念記法の記号全般の説明として前もって述べている。ただ、フレーゲの真理概念の説明は誤っている。もし「真」と「偽」が本当の対象で 〜p 等々におけるアーギュメントであったならば、「〜p 」の意味はフレーゲの規定によっては決して規定されないだろうから。）
4.44	件の符号「W」と諸真理可能性の対応づけによって生じる記号はひとつの文記号だ。
4.441	記号「W」と「F」の複合体に対応する対象（または諸対象の複合体）など無いことは明らかだ。それは横線と縦線や括弧に対応するものなど無いのと同断だ。――「論理的対象」などというものは存在しない。 同様のことは、もちろん、「W」と「F」の図式と同じことを表現する総ての記号に当てはまる。
4.442	例えば、これは文記号だ。 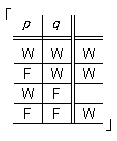（フレーゲの「判断線」「」は論理的に全く無意義〔bedeutungslos〕だ。それは、フレーゲ（とラッセル）のもとでは、ただ、これらの著者がそうして表示された文を真だと考えるということを呈示するだけだ。「」は、だから、例えば文の番号と同様、文構造には属さない。ひとつの文が自らについて、それが真だと言明することなどあり得ない。） 件の図式における真理可能性の順番がひとつのコンビネーション規則によってはっきり定められていれば、最後のコラムはそれだけでもう当の諸真理可能性の表現だ。そのコラムを列として書けば、先の文記号は 「(W W - W)(p, q )」 あるいは、もっとはっきり 「(W W F W)(p, q )」 となる。 （左側の括弧の中の座の数は右側の括弧の中の項の数によって規定される。）
4.45	n 箇の基本的文については、諸真理条件の可能なグループが Ln 箇存在する。 幾つかの基本的文の全真理可能性の一部を成す諸真理条件のグループ全体は、ひとつの列に並べられ得る。
4.46	諸真理条件の可能なグループ全体のうちには、ふたつの極端なケースが存在する。 ひとつのケースでは、当の文は当の諸基本的文の総ての真理可能性について真だ。我々はそうした真理条件はトートロジカルだと言う。 第二のケースでは、当の文は総ての真理可能性について偽だ。つまり、そうした真理条件はコントラディクトリだ。 第一のケースにおける文を我々はトートロジーと呼び、第二のケースではコントラディクションと呼ぶ。
4.461	文はそれが述べることがらを示す。トートロジーとコントラディクションはそれらが何も述べないことを示す。 トートロジーは真理条件をひとつももたない。それは無条件に真なのだから。また、コントラディクションはどんな条件のもとでも真ではない。 トートロジーとコントラディクションは無意味〔sinnlos〕だ。 （そこからふたつの矢印が反対方向に岐れている点のように。） （例えば、私は、雨が降っているか降っていないかのどちらかであることを諒解していても、当の天気については何も諒解していない。）
4.4611	トートロジーとコントラディクションは、だが、ナンセンスではない。それらは当のシンボリズムに属している。それも、「0」が算術のシンボリズムに属すのと同じように。
4.462	トートロジーとコントラディクションは現実の像ではない。それらは何の可能な状況も表わさない。トートロジーはあらゆる可能な状況を許容し、コントラディクションはひとつも許容しないのだから。 トートロジーにおいては、世界との一致の条件――表わしの関係〔die darstellenden Beziehungen〕――の総ては互いに帳消しにし合う。そのためトートロジーは世界に対してどんな表わしの関係にもない。
4.463	ひとつの文の全真理条件は、当の文によって事実全般に許容される遊びの範囲を規定する。 （文、像、模型は、ネガティヴな意味では、他の物体の運動の自由を制限する硬い物体のようであり、ポジティヴな意味では、そこに或る物体が在り処をもつような、硬い物質で境界づけられた空間のようだ。） トートロジーは現実に対して論理的空間全体――無限の――を許容する。コントラディクションは論理的空間全体を充たし、現実に対してひとつの点も許容しない。どちらも、だから、現実を規定することなど到底あり得ない。
4.464	トートロジーの真理性は確実であり、文の真理性は可能、コントラディクションの真理性は不可能だ。 （確実、可能、不可能。ここで我々は、確率論で必要とする例の等級づけの先触れを手にしている。）
4.465	ひとつのトートロジーとひとつの文の論理積は、その文と同じことを述べる。だから、当の積はその文と同一だ。ひとは、シンボルの意味を変えずに、当のシンボルの本質を成すものを変えることはできないのだから。
4.466	諸記号の特定の論理的結びつきには、それらの記号の意義の特定の論理的結びつきが対応する。あらゆる任意の結びつきは、もっぱら結びつけられていない諸記号に対応する。 つまり、あらゆる状況に対して真であるような文は、諸記号の結びつきなどでは全然あり得ない。もしそんなことがあり得たならば、その結びつきには諸対象の特定の結びつきしか対応し得ないだろうから。 （また、諸対象の結びつきで何の論理的結びつきにも対応しないものなど無い。） トートロジーとコントラディクションは諸記号の結びつきの境界ケース、つまり結びつきの解消だ。
4.4661	もちろん、トートロジーとコントラディクションにおいても当の諸記号は互いに結びつけられてはいる。つまり、互いに関係し合っている。だが、それらの関係は無意義であり、当のシンボルには非本質的だ。
4.5	いまや最も一般的な文形式を挙げることが可能なようだ。つまり、何か或る記号言語の文全般の特徴を記述することが。どんな可能な意味もその記述が当てはまる何らかのシンボルによって表現され得る一方、その記述が当てはまるようなどんなシンボルも、その諸名称の意義が適当に選択されれば、何らかの意味を表現し得るように、だ。 その最も一般的な文形式の記述に際しては、ただその本質を成すことがらだけが記述されることを許されるのは明らかだ。――そうでなければ、それは最も一般的な文形式などではないだろう。 最も一般的な文形式が存在することは、その形式をひとが予見（つまり構成）し得なかったような文が存在するのは許されないことによって証明される。その文の一般的形式はこれだ： かくかくしかじかとなっている。
4.51	私に総ての基本的文が与えられているとする。そこで単純にこう問い得る： どんな文を私はそれらからつくることができるのか。ところが、総ての文がそうであり、それらはそうして限定されている。
4.52	あらゆる基本的文の総体から（そして、もちろん、それがあらゆる基本的文の総体であることから）結果的に生じるもの総てが文だ。（だから、ひとは、或る意味で、総ての文は諸基本的文の一般化だと言い得るだろう。）
4.53	その一般的文形式は変数だ。
5	ひとつの文は特定の諸基本的文の真理関数だ。 （基本的文はそれ自体の真理関数だ。）
5.01	当の基本的文のそれぞれがその文の真理アーギュメントだ。
5.02	関数のアーギュメントを名称のインデクスと混同するのはもっともなことだ。私は、アーギュメントによってもインデクスによっても、それらを含む記号の意義〔die Bedeutung〕を認識するのだから。 例えば、ラッセルの「+c 」において、「c 」は当の記号全体がカーディナル数のための加法記号であることを指示するインデクスだ。だが、この表示は恣意的な合意に基いており、ひとは「+c 」ではなくて何らかの単純記号を採ることもできただろう。一方、「〜p 」において、「p 」はインデクスではなくアーギュメントだ。「〜p 」の意味は、「p 」の意味が先に理解されることが無ければ、理解され得ないだろうから。（ユーリウス・カエサルという名称において「ユーリウス」はインデクスだ。インデクスは恒に、我々がその名称に当のインデクスを附ける対象の何らかの記述の一部だ。例えば、ユーリウス一族のそのカエサル〔Der Cäsar aus dem Geschlechte der Julier〕。） アーギュメントとインデクスの混同は、私の思い違いでなければ、文と関数の意義についてのフレーゲの理論の基礎を成している。フレーゲにとって、論理の文は名称であり、そのアーギュメントは当の名称のインデクスだった。
5.1	特定の諸真理関数はひとつの列に並べられ得る。 これが確率論の基礎だ。
5.101	特定の諸基本的文の全真理関数は、当の基本的文の数が幾つであれ、次のような類の図式に書き出され得る。 (W W W W)(p, q ) トートロジー （p ならば p 、そして q ならば q 。）（p ⊃ p . q ⊃ q ） (F W W W)(p, q ) 言葉にすれば： p かつ q 、ということはない。（〜(p . q )） (W F W W)(p, q ) 〃 q ならば p 。（q ⊃ p ） (W W F W)(p, q ) 〃 p ならば q 。（p ⊃ q ） (W W W F)(p, q ) 〃 p または q 。（p ∨ q ） (F F W W)(p, q ) 〃 非 q 。（〜q ） (F W F W)(p, q ) 〃 非 p 。（〜p ） (F W W F)(p, q ) 〃 p または q 、だが両方ともということはない。（p . 〜q : ∨ : q . 〜p ） (W F F W)(p, q ) 〃 p ならば q 、そして q ならば p 。 （p ≡ q ） (W F W F)(p, q ) 〃 p (W W F F)(p, q ) 〃 q (F F F W)(p, q ) 〃 非 p かつ非 q 。（〜p . 〜q ）あるいは（p | q ） (F F W F)(p, q ) 〃 p かつ非 q 。（p . 〜q ） (F W F F)(p, q ) 〃 q かつ非 p 。（q . 〜p ） (W F F F)(p, q ) 〃 p かつ q 。（p . q ） (F F F F)(p, q ) コントラディクション （p かつ非 p 、そして q かつ非 q 。）（p . 〜p . q . 〜q ） ひとつの文を真とするようなその全真理アーギュメントの真理可能性のそれぞれを、私は当の文の真理根拠と呼びたい。
5.11	幾つかの文に共通する真理根拠の総てが或る文の真理根拠でもあるとき、我々は、その文の真理性は件の諸文の真理性から帰結する、と言う。
5.12	特に、文「p 」の真理性が別の文「q 」の真理性から帰結するのは、第二の文の総ての真理根拠が第一の文の真理根拠である場合だ。
5.121	一方の真理根拠全体が他方の真理根拠全体に含まれており、p が q から帰結する。
5.122	p が q から帰結するならば、「p 」の意味は「q 」の意味に含まれている。
5.123	神のようなものが、そこにおいて或る種の文が真であるようなひとつの世界を創造するとき、彼は、そうすることで、さらに、そこにおいて当の諸文から帰結する総ての文が正しいような世界をもう創っている。また、彼は、そこにおいて文「p 」が真であるような何らかの世界を、その対象全体を創ること無く、創ることはできないだろう。
5.124	ひとつの文は、それから帰結するあらゆる文を肯定する。
5.1241	「p . q 」は、「p 」を肯定する文のひとつであるとともに、「q 」を肯定する文のひとつでもある。 ふたつの文は、それらをともに肯定する有意味な文がひとつも存在しないとき、互いに反対だ。 或る文に矛盾する文は何れもその文を否定する。
5.13	或る文の真理性が他の諸文の真理性から帰結することを、我々はそれらの文が成す構造から見て取る。
5.131	或る文の真理性が他の諸文の真理性から帰結するならば、そのことは、それらの文の形式が互いに対して立っている諸関係を通じて自ずと現われる。しかも、我々は、それらの文を結び合わせてひとつの文にすることによって、それらの形式をあらためて当の諸関係に据えるには及ばない。それらの関係は内的であり、当の諸文が存立するや否や、そしてそのことによって、存立する。
5.1311	我々が p ∨ q と 〜p から q を推論するとき、「p ∨ q 」および「〜p 」の文形式間の関係は、この場合、当の表示法によって覆い隠される。だが、例えば、「p ∨ q 」に替えて「p | q . | . p | q 」、「〜p 」に替えて「p | p 」（p | q = 非 p かつ非 q ）と書けば、件の内的関聯は明らかになる。 （ひとが (x ) . fx から fa を推論し得ること、それは一般性が「(x ) . fx 」というシンボルのうちにも在ることを示している。）
5.132	p が q から帰結するならば、私は q から p を推論することができる。q から p を導出することが。 その推論の方法はもっぱら両文から察知され得る。 ただそれらの文自体だけが当の推論を正当化することができる。 推論全般を正当化するとされる――フレーゲとラッセルのもとでのように――「推論法則」などというものは無意味であり、そして無用だろう。
5.133	総ての導出はアプリオリにおこなわれる。
5.134	ひとつの基本的文からは、他のどんな基本的文も導出され得ない。
5.135	何か或る状況の存立から、それとは全く異なる何らかの状況の存立が推論されることなど、到底あり得ない。
5.136	そうした推論を正当化するような因果連鎖なるものは存在しない。
5.1361	我々は、未来の出来事を現在の出来事から推定することはできない。 因果連鎖への信頼が迷信だ。
5.1362	意志の自由は、未来の行動が今現在は把握され得ない点に在る。我々が未来の行動を把握し得るのは、因果が論理的推論の必然性のような内的必然性であるとき、ただそのときだけだろう。――把握と把握されていることがらの関聯は、論理的必然性の関聯だ。 （「A は p が成り立っていることを把握している」は、p がトートロジーの場合、無意味だ。）
5.1363	ひとつの文が我々にとって明白であることから当の文が真であることが帰結しないならば、その明白さは、当の文の真理性への我々の信念に対する何の正当化でもない。
5.14	或る文が別の或る文から帰結するならば、あとの文ははじめの文よりも多くを述べ、はじめの文はあとの文よりも僅かしか述べない。
5.141	p から q が帰結し q から p が帰結するならば、それらは同一の文だ。
5.142	トートロジーは総ての文から帰結する。それは何も述べないのだから。
5.143	コントラディクションは、文全般に共通するもの、どんな文もそれを他の一切の文と共有していないものだ。トートロジーは互いに何も共有していないような文の総てに共通するものだ。 コントラディクションは謂わば総ての文の外に消失し、トートロジーは内に消失する。 コントラディクションは文全般の外的境界であり、トートロジーは実体の無い中心だ。
5.15	Wr が文「r 」の真理根拠の数で、Wrs が「r 」の真理根拠であるとともに文「s 」の真理根拠でもあるものの数であるとき、我々はそれらの比 Wrs ： Wr を文「r 」が文「s 」に与える確率の測度と呼ぶ。
5.151	Wr を先の No. 5.101 の図式と同様の図式での文 r における「W」の数だとし、Wrs を文 s における「W」のうちで、文 r の「W」と同じコラムに位置するものの数だとすれば、文 r は文 s に Wrs ： Wr の確率を与える。
5.1511	確率文全般に特有の特殊な対象など存在しない。
5.152	ひとつの真理アーギュメントも互いに共有していない諸文を、我々は互いに独立していると言う。 ふたつの基本的文は互いに 1/2 の確率を与える。 p から q が帰結するならば、文「q 」は文「p 」に 1 の確率を与える。論理的推論の確実性は確率の一境界ケースだ。 （トートロジーとコントラディクションへの適用。）
5.153	文はそれ自体では蓋然的でも非蓋然的でもない。出来事は現実のものとなるかならないかだ。どっちつかずの出来事など存在しない。
5.154	ひとつの箱の中に同数の白い球と黒い球が在る（そして他には何も無い）とする。私はその箱から一度にひとつづつ球を取り出しては、またもとに戻す。そうすると、私はこの試みによって、取り出しが続くに連れて、取り出された白い球と黒い球の数が互いに近づいていくのを確かめることができる。 これは、だから、数学的事実ではない。 そこで、私が白い球を取り出すだろうことと黒い球を取り出すだろうことは等しく蓋然的だ、と私が言うならば、それは、私が知っている（仮設的に採られた諸自然法則を含む）シチュエーションは何れも一方の出来事の生起に対して他方の生起に対するよりも大きな確率を与えはしないということを意味する。つまり、そうしたシチュエーションは――先の説明から容易に察知され得るように――それぞれの出来事に 1/2 の確率を与える。 私が件の試みによって確認するのは、どちらの出来事の生起も私が特に精しく知っている訳ではない特定の諸シチュエーションとは独立しているということだ。
5.155	確率文の単位はこれだ： 特定の諸シチュエーション――私が特によく知っている訳ではない特定の諸シチュエーション――は或るひとつの出来事の生起にしかじかの程度の確率を与える。
5.156	そんな訳で、確率は一種の一般化だ。 それは何らかの文形式の一般的記述を伴う。 単に確実性が無いために、我々は確率を用いる。――我々はひとつの事実を完璧には知らなくても、その形式については何ごとかを把握しているのだ。 （ひとつの文は、たしかに或る状況の不完全な像であり得るが、しかし、それは恒に一個の完全な像だ。） ひとつの確率文は謂わば他の諸文の要約だ。
5.2	特定の諸文の構造は互いに内的諸関係にある。
5.21	我々はそうした内的関係を、我々の表現方法において、ひとつの文を、別の諸文からそれを生み出す或るオペレーションの結果として表わすことによって、際立たせることができる。（もとになる文のそれぞれをそのオペレーションの基底と言う。）
5.22	オペレーションは、その結果と諸基底の構造間の或る関係の表現だ。
5.23	ひとつの文から別の文を齎すために、その文に為される必要があること、それがオペーレーションだ。
5.231	それは、もちろん、それらの文の形式的諸属性に、それらの形式の内的類似性に依存するだろう。
5.232	ひとつの列を順序づける内的関係は、それによってひとつの項から別の或る項が生じるようなひとつのオペレーションと同等だ。
5.233	オペレーションというものは、或る文が論理的に有意義な〔bedeutungsvolle〕仕方で別の或る文から生じるところに初めて出現し得る。したがって、文の論理的構成がはじまるところに。
5.234	特定の諸基本的文の真理関数は何れも当の諸基本的文を基底としてもつ何らかのオペレーションの結果だ。（私はそうしたオペレーションを真理オペレーションと呼ぶ。）
5.2341	p の真理関数の意味は p の意味の関数だ。 否定、論理和、論理積等々はオペレーションだ。 （否定は文の意味を反対にする。）
5.24	ひとつのオペレーションは何らかの変数において自ずと顕現する。それは、ひとがどうやって諸文がもつ或る形式から別の或る形式に到り得るかを示す。 それは当の諸形式の違いを表現する。 （そして、オペレーションの諸基底こそ、当のオペレーションの諸基底と結果の間に共通するものだ。）
5.241	ひとつのオペレーションは何の形式もマークせず、ただ当の諸形式の違いだけをマークする。
5.242	「p 」から「q 」を齎すオペレーションと同じものが「q 」から「r 」を齎し、以下同様。このことは、もっぱら「p 」、「q 」、「r 」等々が或る種の形式的関係を一般的に表現する変数である点において表現され得る。
5.25	オペレーションの存在が文の意味を特徴づけることはない。 オペレーションは何ごとも言明しはしないのであり、ただその結果だけが何ごとかを言明する。そして、このことは当のオペレーションの諸基底に依存する。 （オペレーションと関数が混同されることは許されない。）
5.251	関数は自らのアーギュメントではあり得ないが、しかし、オペレーションの結果は当のオペレーションそのものの基底になり得る。
5.252	もっぱらそうして、或る形式列における項から項への（ラッセルとホワイトヘッドのヒエラルヒーにおけるタイプからタイプへの）進展は可能だ。（ラッセルとホワイトヘッドは、この進展の可能性を認めていないにもかかわらず、繰り返しそれを使っている。）
5.2521	ひとつのオペレーションの結果そのものに当のオペレーションを続けて適用することを、私はそのサクセッシヴな〔succesive〕適用と呼ぶ（「O 'O 'O 'a 」は「O 'ξ 」の「a 」への三回のサクセッシヴな適用の結果だ）。 同様の意味で、私は複数のオペレーションの幾つかの文へのサクセッシヴな適用について語る。
5.2522	そこで、私は形式列 a, O 'a, O 'O 'a, . . . の一般項をこう書く： 「[a, x, O 'x ]」。この括弧表現はひとつの変数だ。この括弧表現の第一項は当の形式列の初項であり、第二項は当の列の任意の項 x の形式、第三項は x から直接帰結する項の形式だ。
5.2523	オペレーションのサクセッシヴな適用という概念は「以下同様」の概念と同等だ。
5.253	或るオペレーションは別の或るオペレーションの効果をキャンセルし得る。或る種のオペレーションは互いに帳消しにし合い得る。
5.254	オペレーションは消滅し得る（例えば「〜〜p 」における否定、〜〜p = p ）。
5.3	総ての文は諸基本的文に対する諸真理オペレーションの結果だ。 ひとつの真理オペレーションは、特定の諸基本的文からひとつの真理関数が生じるその仕方だ。 特定の諸基本的文からそれらの真理関数が生じるのと同様の仕方で、ひとつの真理オペレーションの本質に随って、諸真理関数から或る新たな真理関数が生じる。どんな真理オペレーションも、諸基本的文の諸真理関数からまた諸基本的文の或る真理関数、或る文を生み出す。諸基本的文に対する諸真理オペレーションの結果に対するどんな真理オペレーションの結果も、また、諸基本的文に対する或るひとつの真理オペレーションの結果だ。 どんな文も諸基本的文に対する諸真理オペレーションの結果だ。
5.31	No. 4.31 の図式は、そうすると、「p 」、「q 」、「r 」等々が基本的文でない場合にも何らかの意義をもつ。 そして、No. 4.442 における文記号は、「p 」と「q 」が諸基本的文の真理関数である場合にも、諸基本的文の或る真理関数を表現するということを見て取るのは容易だ。
5.32	総ての真理関数は、諸基本的文への諸真理オペレーションの有限回のサクセッシヴな適用の結果だ。
5.4	ここで、（フレーゲとラッセルの意味での）「論理的対象」、「論理定数」などというものは存在しないことが自ずと明らかになる。
5.41	というのは、諸真理関数に対する諸真理オペレーションの結果で、諸基本的文の同じ真理関数であるようなものは、総て同一だからだ。
5.42	∨、⊃ 等々が右と左等々の意味での関係ではないことは明白だ。 フレーゲとラッセルの論理的「原記号」一般の相互定義可能性は、それらが原記号などではないことをまさに示しており、何の関係も表示しはしないことをいよいよもって示している。 また、我々が「〜」と「∨」を用いて定義する「⊃」は、「∨」を定義するのに「〜」とともに用いるものと同一なことは明らかであり、そして、この「∨」がはじめのものと同一なことも明らかだ。以下同様。
5.43	p というひとつの事実から、それとは別の無限に多くの事実、つまり、〜〜p、〜〜〜〜p、等々が帰結することになるというのは、もともと信じ難いことなのだ。また、論理（数学）の無限箇の文が半ダースの「根本法則」から帰結するというのもそれに劣らず奇妙だ。 ところが、論理の文は総て同じことを述べる。何も述べないのだから。
5.44	真理関数はマテリアルな関数ではない。 例えば、ひとが二重否定によって肯定を生み出し得るとき、否定は肯定のうちに――何らかの意味で――含まれているのか？ 「〜〜p 」は 〜p を否定しているのか、p を肯定しているのか、それとも両方なのか？ 文「〜〜p 」は否定をひとつの対象のように扱ってはいないが、しかし、肯定の可能性は否定のうちに予め定められている。 また、もし「〜」と称される対象が存在したとすれば、「〜〜p 」は「p 」とは別の何ごとかを述べるはずだろう。というのは、その場合、一方の文はとにかく 〜 を扱い、他方は扱わないだろうからだ。
5.441	こうした見かけの論理定数の消滅は、また、「〜(∃x ) . 〜fx 」が「(x ) . fx 」と同じことを、あるいは「(∃x ) . fx . x = a 」が「fa 」と同じことを述べる場合にも起る。
5.442	ひとつの文が我々に与えられているならば、それとともに、それを基底にもつ総ての真理オペレーションの結果ももう齎されている。
5.45	論理的諸原記号が存在するならば、まっとうな論理学は、それらの相対的ポジションを明確にし、そして、それらの存在を正当化する必要がある。論理の諸原記号からの当の論理の構成が明確にならなければならない。
5.451	論理が根本的諸概念をもつならば、それらは互いに独立しているはずだ。ひとつの根本的概念が導入されているならば、それは、そもそもそこにそれが現われ得る総ての結びつきにおいて導入されているはずだ。ひとは、だから、それを、まず或るひとつの結びつきで、そしてまた別の或る結びつきでというように導入することはできない。例えば、否定が導入されているならば、我々はそれを現に「〜p 」という形式の諸文において、「〜(p ∨ q )」や「(∃x ) . 〜fx 」等のような文においてと同じように理解しているはずだ。我々は、それを、まず諸ケースの或るクラスに、そして別の或るクラスにというように導入することは許されない。というのは、その場合、当の意義が両方のケースで同じかどうか疑わしいままだろうし、また、両方のケースで同一の記号結合法を用いる理由など何も無いだろうからだ。 （要するに、原記号全般の導入については、フレーゲ（『算術の諸根本法則』）が諸記号の定義による導入について述べているのと同じことが、必要な変更を経て〔mutatis mutandis〕、当てはまる。）
5.452	論理のシンボリズムにおける新たな便法の導入は恒にゆゆしい出来事なはずだ。論理においては、新たな便法が――謂わば全く無邪気な表情で――括弧の中や脚註において導入されることなど許されない。 （例えば、ラッセルとホワイトヘッドの『プリンキピア・マテマティカ』では、或る種の定義と根本法則は言葉において現われる。何故ここで突然言葉なのか？ このことは正当化を必要とするだろう。それは欠けており、また欠けている他ない。そうした措置は実は不当なのだから。） 一方、或るところで或る新たな便法の導入が必要なことが明らかになっているならば、ひとはとにかくただちにこう自問しなければならない： この便法はそれにしてもいったい何処で適用される必要があるのか？ 論理におけるそのポジションがとにかく説明される必要がある。
5.453	論理の総ての数は正当化される必要がある。 むしろ、論理においては数など存在しないことが判明するに違いないのだ。 特別な数など存在しない。
5.454	論理においては並存など存在しない。クラス分けなど存在し得ない。 論理においては比較的一般的なものに比較的特殊なものなど存在し得ない。
5.4541	論理的問題全般の解決は単純なはずだ。それらが単純さのスタンダードを設定するのだから。 人間はいつも、その答え全般が――アプリオリに――シンメトリカルであり、完結した規則正しい構成体に統一されているような、そんな或る問題領域が存在するはずだと漠然と感じてきた。 単純さは真理の印〔Simplex sigillum veri〕という格言が当てはまる領域。
5.46	論理記号全般を適切に導入したならば、ひとはそれによってもう既にそれらのコンビネーションの総ての意味を導入し了えていることだろう。だから、「p ∨ q 」だけでなく「〜(p ∨ 〜q )」等々も既に。ひとはまたそれとともに既に可能な限りの括弧のコンビネーションの総ての効果を導入し了えていることだろう。そして、それとともに、本来の一般的原記号は「p ∨ q 」や「(x ) . fx 」等々ではなく、それらのコンビネーションがもつ最も一般的な形式であることが明らかになっていることだろう。
5.461	∨ や ⊃ のような論理的な見かけの関係は括弧を必要とする――本当の関係とは対照的に――という一見ささいな事実は重要だ。 そうした見かけの原記号に対する括弧の利用は、それらが本当の原記号ではないことをまさに指し示しているのだ。それに、括弧が何らかの自立的意義をもつなどとは、きっと誰も考えないだろう。
5.4611	論理的オペレーション記号は一種の句読点だ。
5.47	総ての文がもつひとつの形式についてそもそもはじめから述べられ得ることがらの総ては、一挙に述べられ得るはずなのは明らかだ。 ひとつの基本的文には総ての論理的オペレーションがもう含まれているではないか。「fa 」は 「(∃x ) . fx . x = a 」 と同じことを述べるのだから。 合成性が在ればアーギュメントと関数が在り、アーギュメントと関数が在れば既に総ての論理定数が在る。 ひとはこう言うかも知れない： 総ての文が本性上互いに共有しているものが、唯一の論理定数だ。 それは、だが、一般的文形式だ。
5.471	一般的文形式は文の本質だ。
5.4711	文の本質を特定するとは、総ての記述の本質を特定することを意味する。したがって、世界の本質を。
5.472	最も一般的な文形式の記述は、論理の唯一の一般的原記号の記述だ。
5.473	論理は自らの面倒は自らでみるはずだ。 可能な記号はまた〔何かを〕表示し得るはずだ。論理において可能なことがらはまた許されてもいる。（「ソクラテスは同一である」は、「同一」と呼ばれる属性など存在しないため、何も意味しない。この文はナンセンスだ。それは、我々が何の恣意的な規定も為していなかったからであり、件のシンボルがもっぱらそれ自体で許されていないからではない。） 我々は、或る意味で、論理においては誤り得ない。
5.4731	ラッセルがしきりに語ったあの自明性は、言語そのものがあらゆる論理的誤りを阻むというただそれだけのことによって、論理においては不要になり得る。――論理がアプリオリであることは、何も非論理的には考えられ得ない点に在る。
5.4732	我々は記号に不適切な意味を与えることはできない。
5.47321	オッカムの標語は、もちろん、恣意的な、あるいはその実践的成果によって正当化されるような規則ではない。それは、余分な記号単位は何も指さない、ということを述べているのだ。 同じ目的を果たす諸記号は論理的に同等であり、何の目的も果たさない記号は論理的に無意義だ。
5.4733	フレーゲはこう言う： 適切に形成された文は何れも何らかの意味〔einen Sinn〕をもつはずだ。一方、私はこう言う： 可能な文は何れも適切に形成されており、もしそれが何の意味ももたないならば、それは我々がその成分の幾つかに何の意義〔Bedeutung 〕も与えていなかったせいでしかあり得ない。 （たとえ我々がそうしたと信じているとしても。） 例えば、「ソクラテスは同一である」は、我々が「同一」の語に形容詞としての何の意義も与えていなかったのだから、何も述べはしない。というのは、この語は、それが等号として現われる場合、全く別の仕方でシンボライズするのであり――それが表示している関係は何か別のものであり、――したがって、当のシンボルも両ケースで全く異なるからだ。両シンボルはたまたま当の記号を共有しているだけだ。
5.474	必要な根本的オペレーションの数は、もっぱら我々の表記法にかかっている。
5.475	大事なのは、ただ、特定の次元数をもつ――特定の数学的多様性をもつ――記号システムをつくることだ。
5.476	ここで問題になっているのは、表示される必要がある根本的概念の数ではなくて、何らかの規則の表現であることは明らかだ。
5.5	あらゆる真理関数は、オペレーション (- - - - - W)(ξ, . . . . ) の諸基本的文へのサクセッシヴな適用の結果だ。 このオペレーションは右の括弧内の文全部を否定する。それを私はそれらの文の否定と呼ぶ。
5.501	その項が何れも何らかの文であるような括弧表現を、私は――その括弧内での当の諸項の順番はどうでもいい場合――「()」という形式の記号によって示唆する。「ξ 」は変数であり、その値は何れも当の括弧表現の項だ。また、この変数の上の線は、当の変数が括弧内のその値全部を代表することを示唆する。 （だから、例えば ξ が三つの値 P、Q、R をもてば、() = (P, Q, R ) となる。） この変数の値全般は約定される。 その約定は、当の変数が代表する諸文の記述だ。 当の括弧表現の諸項の記述がどう為されるかは非本質的だ。 我々はそうした記述を三種類に分けることができる。1. 直接の枚挙。このケースでは、我々は、変数ではなく、単純にその一定の諸値を置くことができる。2. 或る関数 fx の陳述。x のどんな値に対するその値も記述すべき当の文であるような、そんな関数の。3. 或る形式的法則の陳述。それに随って当の諸文が形成されているような、そんな法則の。このケースでは、当の括弧表現の諸項は或る形式列の項全部だ。
5.502	私は、そこで、「(- - - - - W)(ξ, . . . . )」に代えて「N()」と書く。 N() は文変数 ξ の値全部の否定だ。
5.503	或る種の文がこのオペレーションによって如何に形成され得るか、また、或る種の文がそれによってはどうして形成され得ないかは明らかに容易に表現され得るのだから、このことは何らかの正確な表現をさらに与えられ得るはずだ。
5.51	がただひとつの値をもつ場合、N() = 〜p （非 p ）となり、ふたつの値をもつ場合には、N() = 〜p . 〜q （非 p かつ非 q ）となる。
5.511	総てを捉え、世界を映す論理が、こんな特殊な鈎と小細工をどうして用い得るのか？ もっぱら、それらの総てが限り無く精緻なひとつのネットワークに、巨大な鏡に結びついていることによって。
5.512	「〜p 」が真なのは、「p 」が偽なときだ。だから、真な文「〜p 」において、「p 」は偽な文だ。そうすると、線「〜」はどうしてこの文を現実に一致させ得るのか？ 「〜p 」において否定するのは、だが、「〜」ではなくて、この表記法の記号で p を否定するようなものの総てに共通するものだ。 それは、だから、それによって「〜p 」、「〜〜〜p 」、「〜p ∨ 〜p 」、「〜p . 〜p 」等々が（無限に〔ad inf.〕）形成される共通規則だ。そして、この共通のものが否定を反映する。
5.513	ひとはこう言い得るだろう： p と q をともに肯定するような総てのシンボルに共通するものは文「p . q 」であり、p か q かを肯定するような総てのシンボルに共通するものは文「p ∨ q 」だ。 また、ひとはこう言い得る： ふたつの文は、それらが何も共有していないならば、互いに反対であり、また、ひとつの文に対して全くその外に位置する文はひとつしか存在しないから、どんな文もただひとつのネガティヴをもつ。 これでラッセルの表記法においても「q : p ∨ 〜p 」は「q 」と同じことを述べること、そして、「p ∨ 〜p 」は何も述べないことが自ずと明らかになる。
5.514	何らかの表記法が定められていれば、そこには、p を否定する文の総てがそれによって形成されるような規則が存在し、p を肯定する文の総てがそれによって形成されるような規則が存在し、p か q を肯定する文の総てがそれによって形成されるような規則が存在し、以下同様。これらの規則は当の諸シンボルと同等であり、そして、それらには当の諸シンボルの意味が反映している。
5.515	「∨」や「 . 」等々によって結び合わされるのは諸文でしかあり得ないことは、我々のシンボル全般に自ずと顕現するはずだ。 そして、実際そのとおりだ。シンボル「p 」や「q 」そのものが「∨」や「〜」等々を前提とするのだから。「p ∨ q 」における記号「p 」がどんな複合的記号も代表していないならば、それは単独では意味をもち得ないが、そうすると、しかし、「p 」と同じ意味をもつ記号「p ∨ p 」や「p . p 」等々もまた何の意味ももち得ない。ところが、「p ∨ p 」が何の意味ももたないならば、「p ∨ q 」もまた何の意味ももち得ない。
5.5151	ネガティヴな文の記号はポジティヴな文の記号から形成されなければならないのか？ 何故ひとはネガティヴな文をネガティヴな事実によって表現し得ないのだろう。（例えば、「a 」が「b 」に対して或るひとつの関係にない場合、そのことは aRb が成り立たないことを表現し得るかも知れない。） だが、やはりその場合でも、ネガティヴな文はポジティヴな文を通じて非直接的に形成されているのだ。 ポジティヴな文はネガティヴな文の存在を前提とせざるを得ず、逆もまた成り立つ。
5.52	ξ の値全体が或る関数 fx の x のあらゆる値についての値全部ならば、N() = 〜(∃x ) . fx となる。
5.521	私は総てという概念を真理関数から切り離す。 フレーゲとラッセルは一般性を論理積ないし論理和との結びつきにおいて導入している。そのため、両方の観念がそれらのうちに封じられている文「(∃x ) . fx 」や「(x ) . fx 」を理解するのが困難になった。
5.522	一般性表示に特有なのは、第一に、それが或る論理的プロトタイプを指し示すことであり、第二に、それが諸定数を際立たせることだ。
5.523	一般性表示はアーギュメントとして現われる。
5.524	一定の諸対象が齎されているならば、それらとともに総ての対象がもう既に我々に与えられている。 一定の諸基本的文が齎されているならば、それらとともに総ての基本的文がもう齎されている。
5.525	文「(∃x ) . fx 」を――ラッセルがそうしているように――「fx は可能である」によって言葉に表わすのは不当だ。 或る状況の確実性なり可能性なり不可能性なりは、文によってではなくて、或る表現がトートロジーなり有意味な文なりコントラディクションなりであることによって表現される。 ひとがきまって引き合いに出したがるかの先例は、当のシンボルそのもののうちに既に在るはずだ。
5.526	ひとは完璧に一般化された諸文によって世界を完全に記述し得る。つまり、そもそも何か或る名称を特定の対象に対応づけるようなこと無く。 さらに通常の表現法に到るためには、ひとは「・ ・ ・ のようなただひとつの x が存在する」というような表現のあとに、そしてその x は a である、と言う必要があるだけだ。
5.5261	完璧に一般化された文は、他のあらゆる文と同様、合成されている。（このことは、我々が「(∃x, φ ) . φx 」において「φ 」と「x 」に別々に言及する必要がある点に自ずと顕現する。どちらも、一般化されていない文においてと同様、独立して世界との表示関係に在る。） 合成されたシンボルの徴： それは何かを他の諸シンボルと共有している。
5.5262	どんな文の真偽も世界の一般的構造がもつ何かを変えるのだ。そして、基本的文の総体によって世界の構造に許容される遊びの範囲それこそが、全く一般的な文全般が劃すものだ。 （或る基本的文が真であれば、それとともに少なくとももうひとつの基本的文が真だ。）
5.53	対象の同一性を私は記号の同一性によって表現する。等号なるものの援けにはよらない。対象間の相違は記号間の相違によって。
5.5301	同一性が対象間の関係ではないことは明らかだ。それは、ひとが例えば文「(x ) : fx . ⊃ . x = a 」を考察すれば顕著になる。この文が述べているのは、a だけが関数 f を充たすということに過ぎず、a に対して或る関係をもつようなものだけが関数 f を充たすということではない。 ひとは、もちろん、ここで、まさに a だけが a に対してこの関係をもつ、と言い得るだろうが、しかし、それを表現するためには、我々は等号そのものを必要とする。
5.5302	ラッセルの「=」の定義は十分ではない。ひとは、それに随えば、ふたつの対象が総ての属性を共有すると言うことができないのだから。（決して正しくはないにしても、やはりこの文は意味をもつ。）
5.5303	大雑把に言えば、ふたつのものについてそれらが同一だと言うことはナンセンス〔ein Unsinn〕というものであり、ひとつのものについてそれがそれ自体と同一だと言うことは全く何も述べていない。
5.531	私は、だから、「f (a, b ) . a = b 」ではなく、「f (a, a )」（あるいは「f (b, b )」）と書く。また「f (a, b ) . 〜a = b 」ではなく「f (a, b )」と。
5.532	また同様に、「(∃x, y ) . f (x, y ) . x = y 」ではなく「(∃x ) . f (x, x )」と、そして「(∃x, y ) . f (x, y ) . 〜x = y 」ではなく「(∃x, y ) . f (x, y )」と。 （したがって、ラッセル流の「(∃x, y ) . f (x, y )」に替えて「(∃x, y ) . f (x, y ) . ∨ . (∃x ) . f (x, x )」と。）
5.5321	したがって、「(x ) : fx ⊃ x = a 」に替えて我々は例えば「(∃x ) . fx . ⊃ . fa : 〜(∃x, y ) . fx . fy 」と書く。 また、「ただひとつの x だけが f ( ) を充たす」という文は「(∃x ) . f x : 〜(∃x, y ) . fx . fy 」だ。
5.533	等号は、だから、概念記法の本質的成分ではない。
5.534	そして、いま、「a = a 」、「a = b . b = c . ⊃ a = c 」、「(x ) . x = x 」、「(∃x ) . x = a 」等々のような見かけの文はどんなまっとうな概念記法においても全く書下され得ないことが、我々には判る。
5.535	それとともに、そうした見かけの文に結びつけられていた総ての問題ももう片がつく。 ラッセルの「無限公理」に伴う総ての問題は、これでもう解かれ得る。 無限公理が述べているとされることがらは、相異なる意義をもつ無限に多くの名称が存在することを通じて、言語において自ずと現われることだろう。
5.5351	ひとが「a = a 」なり「p ⊃ p 」なりといった形式の表現を利用したい誘惑に駆られるような或る種のケースが存在する。しかも、それは、ひとがプロトタイプ、つまり、文、もの等々について語ろうとするときに起る。例えば、ラッセルは、『数学の諸原理』において、「p は文である」というナンセンス〔den Unsinn〕を「p ⊃ p 」によってシンボルに表わし、或る種の文の前に仮定として置いている。それらのアーギュメントの座がもっぱら諸文によって占められ得るように。 （或る文に適切な形式の諸アーギュメントを確保するために仮定 p ⊃ p を当の文の前に置くのはナンセンスというものだ。なにしろ、その仮定は何か文でないアーギュメントに対しては偽ではなくナンセンスになるのだし、当の文も、それ自体が不適切な類のアーギュメントによってナンセンスになるため、自らを不適切なアーギュメント全般から護るということにかけては、その目的で附け足された件の無意味な〔sinnlose〕仮定と同じ役割しか果たさないのだから。）
5.5352	同様に、ひとは「何ものも存在しない」を「〜(∃x ) . x = x 」によって表現しようとすることだろう。だが、たとえこれが文だとしても――それは、また、「諸物が存在する」にはするもののそれらが何れも自己自身と同一ではない場合にも、真なのではないか？
5.54	一般的文形式では、ひとつの文がひとつの文の中に現われるのは、もっぱら諸真理オペレーションの基底としてだ。
5.541	一見、或る文は別の或る文の中に別の仕方でも現われ得るかのようではある。 特に、「A は p が成り立っていると信じている」や「A は p と考える」等々のような心理学の或る種の文形式において。 ここでは、表面的には、文 p が対象 A と或る種の関係にあるかのような訳だ。 （また、現代的認識論（ラッセル、ムーア等々）においても、こうした文は実際そう解されてきた。）
5.542	だが、「A は p ということを信じている」、「A は p と考える」、「A は p と言う」が「「p 」は p と述べる」という形式をもつことは明らかだ。そして、ここで問題なのは、或る事実と或る対象の対応づけではなくて、諸事実の対象間の対応づけを通じての、事実間の対応づけなのだ。
5.5421	このことは、また、今日の皮相な心理学において解されるような魂――主観等々――なるものは馬鹿げていることを示している。 合成された魂など、もはや魂どころではないだろう。
5.5422	「A は p と判断する」という文の形式のまっとうな説明は、ナンセンスというものを判断するのは不可能なことを示すはずだ。（ラッセルの理論はこの条件を充たさない。）
5.5423	ひとつの複合体を知覚するとは、その諸成分が互いにしかじかに係り合っているのを知覚することを意味する。 このことは、ひとが図形 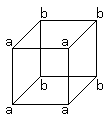を立方体として二通りに見ることができることおよび似たような現象の総てをたしかに説明しはする。我々はとにかく実際にふたつの相異なる事実を見るのだから。 （私がはじめに a の四角を見て、そしてほんのちらりと b を見れば、a が手前に見えるし、逆の場合も同様だ。）
5.55	我々は、ここで、基本的文の総ての可能な形式についての問いにアプリオリに答える必要がある。 基本的文は諸名称から成る。ところが、相異なる意義をもつ名称の数を特定することはできないのだから、我々はまた当の基本的文の構成を特定することもできない。
5.551	我々の原則は、およそ論理によって判定され得る問いは何れもあっさりと判定され得るのでなければならない、ということだ。 （そして、我々がそうした問題に世界を観察することによって答えざるを得ないはめに到ったならば、それは我々が根本的な見当違いをしていることを示している。）
5.552	我々が論理の理解に必要とする「経験」なるものは、何かがしかじかとなっていることではなくて、何かが在ることだ。だが、これはとにかく経験ではないのだ。 論理はあらゆる経験――何かがそうあること――に先行する。 それは如何にに先行する。何にではない。
5.5521	もしそうでなかったならば、どうして我々は論理を適用し得るだろうか？ ひとはこう言い得るだろう： たとえ世界が存在しなくとも何らかの論理は存在するのだとすれば、世界が存在するとき、どうしてさらに別の或る論理が存在し得るだろうか。
5.553	ラッセルは、色々な箇数のもの（個体）の間に単純な諸関係が存在すると言った。だが、どの箇数の間に？ また、それはどう決まるというのか？――経験によって？ （特別な数などというものは存在しない。）
5.554	どんな特殊な形式の陳述も全く恣意的だろう。
5.5541	例えば、私が何ごとかを或る 27 項関係の記号によって表示せざるを得ないはめに到り得るかどうかは、アプリオリに特定され得るという。
5.5542	だが、我々はそもそもそう問うていいものなのか？ 或る記号形式を立てながら、それに何かが対応し得るかどうかは諒解していないということが、我々にはあり得るのか？ 何ごとかが成り立ち得るためには何が在る必要があるのか、という問いは意味をもつのか？
5.555	我々が基本的文を、その特殊な論理的形式とは別に、理解していることは明らかだ。 一方、ひとが或るシステムに拠って諸シンボルを形成し得るとき、そこで論理的に重要なものは当のシステムであり、個々のシンボルではない。 それに、論理において私は私が考案し得る諸形式に関わっているなどということがどうしてあり得るだろうか。そうではなくて、私は私にそれらを考案するのを可能にするものに関わっているはずだ。
5.556	基本的文の形式のヒエラルヒーなどというものは存在し得ない。我々は自らが構成するものだけを予見し得る。
5.5561	経験的実在は対象の総体によって限定されている。その境界は基本的文の総体において再び自ずと顕現する。 ヒエラルヒー全般は実在とは独立しているし、また、そうでなければならない。
5.5562	我々が、純粋に論理的な諸根拠から、諸基本的文が存在するはずであることを把握しているのであれば、文全般を分析されていない形式で理解している者は誰でもそのことを把握しているはずだ。
5.5563	我々の日常言語の文の総ては、実際、そのままで論理的に完璧に秩序づけられている。――我々がここで特定すべき最も単純なものは、真理の喩などではなく、十全な真理そのものだ。 （我々の諸問題は抽象的ではない。たぶん存在する諸問題で最も具体的なものだ。）
5.557	論理の適用がどんな基本的文が存在するかを決める。 その適用のうちに在るものを論理は先取りし得ない。 論理はその適用と衝突してはならない。これは明らかだ。 一方、論理はその適用と合致する必要がある。 だから、論理とその適用は互いに交叉してはならない。
5.5571	私が基本的文全般をアプリオリに特定し得ないならば、それらを特定しようとすることは明白なナンセンスを結果として齎すはずだ。
5.6	私の言語の限界とは私の世界の限界のことだ。
5.61	論理は世界を充たす。世界の限界は論理の限界でもある。 我々は、だから、論理においてこう言うことはできない： これこれは世界の中に存在し、あれは存在しない。 これはつまり我々が或る種の可能性を締め出すことを前提としているようだが、しかし、それは成り立ち得ない。もし成り立ち得たとすれば、つまり、論理が世界の限界を別の側からも観察し得たとすれば、論理は世界の限界を超えていることになるだろうから。 我々は、考え得ないことがらは考え得ない。考え得ないことがらを述べることも、だから、できない。
5.62	この所見は、独我論はどの程度まで真理なのかという問いの判定への鍵になる。 独我論が考えていることは全く正しいが、しかし、それは述べられ得ず、自ずと明らかになるのだ。 世界は私の世界であること、それは、この言語（私がもっぱら理解するこの言語）の限界とは私の世界の限界のことである点に、自ずと顕現する。
5.621	世界と生〔das Leben〕はひとつのものだ。
5.63	私は私の世界だ。（ミクロコスモス。）
5.631	思惟し表象する主観などというものは存在しない。 『私が見出した世界』という本を私が書いたならば、そこには私の体のこともリポートされ、そして、そのどのパーツが私の意志に随い、どれが随わないか等々が述べられることになるだろうが、これは、主観を分離する、というよりむしろ、或る重要な意味で主観など存在しないことを示す一方法なのだ。ただそれだけが、件の本で話題にされ得ないのだから。――
5.632	主観は世界には属さない。それは世界の境界だ。
5.633	世界の何処に形而上学的主観なるものが感知され得るのか？ この場合、眼と視野に関してと全く同様になっている、と君は言う。だが、当の眼を君は実際には見ていない。 また、それが眼によって見られることを推論させるようなものなど視野には何も無い。
5.6331	視野はこんな形式など全然もってはいないのだ。
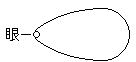5.634	これは、我々の経験のどんな部分もアプリオリではないことに関聯している。 我々が見るものごとの総ては別様でもあり得たことだろう。 およそ我々が記述し得るものごとの総ては別様でもあり得たことだろう。 ものの間のアプリオリな秩序など存在しない。
5.64	ここで、ひとは、独我論は厳密に貫徹されれば純粋な実在論に一致することを見て取る。独我論の自我は広がりのない点にまで縮み、それと並べられていた実在が残る。
5.641	だから、実際、その意味では哲学で自我が非心理学的に話題にされ得るような、そんな意味は存在する。 自我は「世界は私の世界である」ことを通じて哲学のうちに入る。 哲学的自我は人間ではなく、人間の身体でもなければ心理学が扱う人間の魂でもなく、形而上学的主観、世界の―― 一部分ではなく――境界だ。
6	真理関数の一般的形式はこうだ： [, , N()]。 これが文の一般的形式だ。
6.001	これは、どんな文もそれぞれに特定の諸基本的文へのオペレーション N() のサクセッシヴな適用の結果であることを述べているに過ぎない。
6.002	文の組み立てられ方の一般的形式が齎されているならば、それとともに、或る文から或るオペレーションによって別の或る文が如何に生み出され得るかについての一般的形式も、もう齎されている。
6.01	オペレーション Ω'() の一般的形式は、だから、こうだ。 [, N()]'() (= [, , N()]) これは或る文から別の或る文への移行の最も一般的な形式だ。
6.02	そして、我々はこのようにして数に到る： 私は x = Ω0'x　Def. そして Ω'Ων'x = Ων +1'x　Def. と定義する。 そこで、これらの記号規則に随って、我々は列 x, Ω'x, Ω'Ω'x, Ω'Ω'Ω'x, . . . を Ω0'x, Ω0+1'x, Ω0+1+1'x, Ω0+1+1+1'x, . . . と書く。 そこで、私は「[x, ξ, Ω'ξ ]」に代えて「[Ω0'x, Ων'x, Ων +1'ξ ]」と書く。 そして、こう定義する。 0 + 1 = 1　Def. 0 + 1 + 1 = 2　Def. 0 + 1 + 1 + 1 = 3　Def. （以下同様）
6.021	数はひとつのオペレーションの冪指数〔der Exponent〕だ。
6.022	数概念は、総ての数に共通するもの、数の一般的形式に他ならない。 数概念は変数的数だ。 そして、数的同一性の概念は総ての特殊な数的同一性がもつ一般的形式だ。
6.03	整数の一般的形式はこうだ： [0, ξ, ξ + 1]。
6.031	クラス理論は数学においては全く余計だ。 このことは、我々が数学で必要とする一般性は偶然的なものではないことに関聯している。
6.1	論理の文全般はトートロジーだ。
6.11	論理の文全般は、だから、何も述べない。（それらは分析的文だ。）
6.111	論理の何らかの文を内容に充ちているように思わせる理論はきまって誤っている。ひとは、例えば、「真」および「偽」という語は諸属性のうちの或るふたつの属性を特に表示すると考えるかも知れないが、そうすると、どんな文もこれらの属性のひとつをもつことは奇妙な事実に思えることだろう。これは、もう自明どころではなく、例えば「総ての薔薇は黄色か赤かのどちらかである」という文はたとえそれが真だったとしても自明になど響かないだろうが、それと同断に見える。件の文はいまや或る種の自然科学的文のキャラクターをすっかり帯びているのであり、このことは、それが誤って理解された確かな徴候だ。
6.112	論理的文全般のまっとうな説明は、それらに総ての文のうちで或る比類ないポジションを与えるはずだ。
6.113	ひとは論理的文が真なことをそのシンボルだけで認識し得るということは、論理的文全般の特殊なメルクマールであり、また、この事実は論理の哲学全体を自らのうちに封じ込めている。そして、非論理的文の真偽は当の文だけでは認識され得ないということも同じく最重要な事実のひとつだ。
6.12	論理の文全般がトートロジーであること、それは言語の、世界の形式的――論理的――属性全般を示す。 論理の文の諸成分がそのように関聯づけられてトートロジーになることは、当の諸成分の論理を特徴づける。 諸文が特定の仕方で関聯づけられてトートロジーになるためには、それらが特定の構造的諸属性をもっている必要がある。それらがそのように結びつけられてトートロジーになることは、だから、それらがそうした構造的諸属性を有していることを示している。
6.1201	例えば、文「p 」と「〜p 」が「〜(p . 〜p )」という結びつきでトートロジーになることは、それらが互いに矛盾することを示している。文「p ⊃ q 」、「p 」、「q 」が「(p ⊃ q ) . (p ) : ⊃ : (q )」という形式に結び合わされてトートロジーになることは、q が p と p ⊃ q から帰結することを示しており、「(x ) . fx : ⊃ : fa 」がトートロジーであることは fa が (x ) . fx から帰結することを、等々。
6.1202	ひとが、同じ目的のために、トートロジーではなくコントラディクションを用いることもできただろうことは明らかだ。
6.1203	トートロジーをそういうものとして認識するために、ひとは、当のトートロジーに一般性表示が現われないケースでは、次のような具体的方法を利用することができる。私は「p 」、「q 」、「r 」等に代えて「W p F」、「W q F」、「W r F」等と書く。特定の諸真理コンビネーションを私は括弧によって、例えば、 と表現し、文全体の真偽と当の諸真理コンビネーションの対応を線によって次のように表現する。 したがって、この記号は、例えば、文 p ⊃ q を表わすだろう。そこで、私は、例えば、文 〜(p . 〜p )（矛盾律）がトートロジーであるかどうかを、この観点から調べてみたい。「〜ξ 」 という形式は、我々の表記法では、 と書かれ、「ξ . η 」という形式はこう書かれる。 したがって、文 〜(p . 〜q ) はこうなる。 「q 」に換えて「p 」を置いて、最も外側の W および F と最も内側の W および F との結びつきを調べてみれば、当の文全体が真であることはその諸アーギュメントの総ての真理コンビネーションに対応づけられており、偽であることはどんな真理コンビネーションにも対応づけられていないことが判明する。
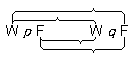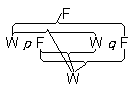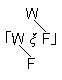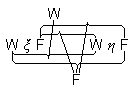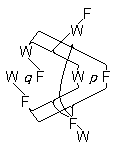6.121	論理の文は、諸文を結びつけて内容の無い文にすることによって、それらの論理的属性をデモンストレートする。 この方法をひとは零位法〔eine Nullmethode〕と呼ぶこともできるだろう。ひとつの論理的文において、諸文は互いに平衡にされ、そして、その平衡状態が、それらの文が論理的にどんな状態にあるはずかを呈示する。
6.122	このことから、我々は論理的文など無しにも済まし得ることが判明する。我々は、適当な表記法において、諸文の形式的属性を当の諸文の単なる外観を通じて認識することができるのだから。
6.1221	例えば、ふたつの文「p 」と「q 」が「p ⊃ q 」という結びつきでトートロジーになるならば、q が p から帰結することは明らかだ。 例えば、「q 」が「p ⊃ q . p 」から帰結することを、我々は両文そのものから察知するが、それを、我々は、また、それらの文を結びつけて「p ⊃ q . p : ⊃ : q 」とし、そして、これがトートロジーであることを示すことによっても、示すことができる。
6.1222	このことは、論理的文全般が経験によって反証され得ないのと同様確証もされ得ないのは何故か、という問いに光を投じる。論理の文は、どんな可能的経験によっても反証され得てはならないばかりか、そうした経験によって確証され得てもならない。
6.1223	いまや、「論理的真理」全般が我々によって「要請」されなければならないかのようにひとがしばしば感じたのは何故かが明らかになる。我々は、十分な表記法を要請し得る限りにおいて、論理的真理全般を要請し得るのだ。
6.1224	また、どうして論理学が形式の、そして推論の学と呼ばれることになったのかも明らかになる。
6.123	ひとつの論理法則そのものがまた何らかの論理法則に従属してはならないことは明らかだ。 （それぞれの「タイプ」にラッセルが考えたように固有の矛盾律が存在する訳ではない。矛盾律は、それ自体には適用されないのだから、ひとつで足りる。）
6.1231	一般的妥当性は論理的文の徴ではない。 一般的であるとは、たまたま総てのものに当てはまることを意味するに過ぎないのだ。一般化されていない文は一般化されている文と全く同様にトートロジカルであり得る。
6.1232	論理的な一般的妥当性を、ひとは、例えば「総ての人間は死ぬべきさだめにある」のような偶然的なものと対照的に、本質的と言うことができるだろう。ラッセルの「還元公理」のような文は論理的文ではない。そして、このことは、そうした文は、真だとしても、もっぱら都合のいい偶然によって真であり得ているだけなのではないか、という我々の感じを説明する。
6.1233	還元公理が通用しないような世界は考えられ得る。だが、論理は我々の世界が実際そうであるか否かという問いには何の関わりもないことは明らかだ。
6.124	論理的文全般は、世界の骨子を記述する、というよりむしろ、表わす。それらは何を「扱う」のでもない。それらは、名称が意義を、そして基本的文が意味をもつことを前提としているが、このことがそれらと世界との結びつきだ。諸シンボルの或る種の――本質的に一定の特徴をもつ――結びつきがトートロジーであることが世界について何かを呈示しているはずなのは明らかだ。この中には決定的なことがらが在る。我々が用いるシンボルには恣意的なところもあればそうでないところもあると我々は言った。論理においてはただ恣意的でないところだけが表現する。これは、だが、論理においては、我々が記号全般の援けによって望みのことがらを表現する訳ではなくて、もとより不可欠な記号全般の本性そのものが言明することを意味する。我々が何か或る記号言語の論理的構文論を知っているならば、論理の文の総ては既に齎されているのだ。
6.125	最初から総ての「真である」論理的文の何らかの記述を与えることは可能だ。しかも、論理の旧い解釈に随ってさえ。
6.1251	だから、論理においてはまた思いがけないことなど決して起り得ない。
6.126	或る文が論理に属すかどうかを、ひとは、当のシンボルの論理的諸属性を計算することで、計算することができる。 そして、それを我々は論理的文を「証明する」ときにおこなっている。我々は、意味や意義など気にかけること無く、ひとつの論理的文を他の諸論理的文から単なる諸記号規則に随って形成するのだから。 論理的文全般の証明は、我々がそれらの文を他の諸論理的文から或る種のオペレーションのサクセッシヴな適用によって生じさせる点に在る。はじめの諸トートロジーから繰り返しトートロジーを生み出すような、そんな諸オペレーションの。（しかも、ひとつのトートロジーからは諸トートロジーだけが帰結する。） もちろん、論理の文全般がトートロジーであることを示すこの方法は、論理には全く非本質的だ。なにしろ、そこから証明がはじまる当の諸文は、証明無しでそれらがトートロジーであることを示さなければならないのだから。
6.1261	論理においてはプロセスと結果は同等だ。（だから、思いがけないことはひとつも無い。）
6.1262	論理における証明は、トートロジーの認識を、それが込み入っている場合でも容易にするための、メカニカルな補助手段に過ぎない。
6.1263	もし、ひとが或る有意味な文を他の有意味な諸文から論理的に証明することができ、さらに何らかの論理的文まで証明することができたとしたら、それはあまりに奇妙というものだろう。有意味な文の論理的証明と論理における証明がふたつの全く別々のことがらであるはずなのは、はじめから明らかだ。
6.1264	有意味な文は何ごとかを言明し、その証明はそのとおりであることを示す。論理においてはどんな文も何らかの証明の形式だ。 論理の文は何れも記号において表わされたモドゥス・ポーネンス〔modus ponens〕だ。（そして、ひとはモドゥス・ポーネンスを文によって表現することはできない。）
6.1265	ひとはいつでも論理のことを、どんな文もそれ自体の証明であるように解し得る。
6.127	論理の文は総て同権だ。それらのうちには根本法則に派生的文など本質的に存在しない。 どんなトートロジーも自らがトートロジーであることを示している。
6.1271	「論理的根本法則」の数が恣意的なことは明らかだ。ひとは論理を、例えば単にフレーゲの諸根本法則の論理積をつくることによって、ひとつの根本法則から演繹することもできただろうから。（フレーゲは、そんな根本法則はもうストレートには理解できない、とおそらくは言うことだろう。だが、フレーゲのような厳格な思索家が、論理的文の基準として理解しやすさの程を引き合いに出すとはおかしい。）
6.13	論理は学説ではなく、世界の鏡像だ。 論理は超越論的だ。
6.2	数学はひとつの論理的方法だ。 数学の文一般は等式であり、したがって、見かけの文だ。
6.21	数学の文は何の思考も表現しはしない。
6.211	我々が生活において必要とするのは、決して数学的文ではないのだ。我々は数学的文をもっぱら数学に属さない諸文から同じく数学に属さない諸文を推論するのに利用する。 （哲学において、「我々はそもそもあの語、あの文を何のために用いるのか」という問いは繰り返し貴重な洞察を齎す。）
6.22	論理の文全般がトートロジーの形をとって示す世界の論理を、数学は等式全般で示す。
6.23	ふたつの表現が等号で結びつけれらるとき、それは、それらが互いに置換可能なことを意味する。だが、それが成り立つかどうかは、両表現そのものに自ずと顕現するはずだ。 ふたつの表現が互いに置換可能なことは、それらの論理的形式を特徴づける。
6.231	ひとがそれを二重否定と解し得ることは、肯定の一属性だ。 ひとがそれを「(1 + 1) + (1 + 1)」と解し得ることは、「1 + 1 + 1 + 1」の一属性だ。
6.232	フレーゲは言う。これらふたつの表現は、同じ意義〔Bedeutung〕をもつが、相異なる意味〔Sinn〕をもつ、と。 等式で本質的なのは、だが、等号が結びつけるふたつの表現が同じ意義をもつことを示すのに当の等式は必要ではないということだ。それは両表現そのものから察知され得るのだから。
6.2321	そして、数学の文一般は証明され得るということが意味するのは、数学の文の正しさは、それが表現していることがらそのものがその正しさの点で事実と比較されるのを必要とすること無く、悟られ得るということに過ぎないのだ。
6.2322	ふたつの表現の意義の同一性は主張され得ない。というのは、それらの意義について何かを主張し得るためには、私はそれらの意義を知る必要があるが、それらの意義を知ることで、私はそれらが同じものを指すのかそれとも別々のものを指すのかを諒解するからだ。
6.2323	等式は、私がそこから当のふたつの表現を考察するその観点、つまり、それらの同義性という観点をマークするだけだ。
6.233	ひとは数学的問題一般の解決に直観を必要とするか、という問いに対しては、まさに言語がここで必要な直観を提供する、という答えが返されるはずだ。
6.2331	計算のプロセスこそがその直観をとりなす。 計算は実験ではない。
6.234	数学は論理の一方法だ。
6.2341	数学的方法の本質を成しているのは、それが諸等式とともにはたらくことだ。数学のあらゆる文が自明なはずであることは、この方法に基いているのだ。
6.24	当の諸等式を得るための数学の方法は、代入法だ。 というのは、等式全般はふたつの表現の置換可能性を表現しており、我々は幾つかの等式から、それらに随って諸表現を別の諸表現に置き換えることで、新たな諸等式へと進むからだ。
6.241	例えば、2 × 2 = 4 という文の証明はこうだ。 (Ων)μ'x = Ων×μ'x　Def. Ω2×2'x = (Ω2)2'x = (Ω2)1+1'x = Ω2'Ω2'x = Ω1+1'Ω1+1'x = (Ω'Ω)'(Ω'Ω)'x = Ω'Ω'Ω'Ω'x = Ω1+1+1+1'x = Ω4'x
6.3	論理の探求とは総ての法則性の探求のことだ。そして、論理の外では総てが偶然だ。
6.31	いわゆる帰納法則は、とにかく論理法則ではあり得ない。それは明らかに有意味な文なのだから。――したがって、それはアプリオリな法則でもあり得ない。
6.32	因果法則は法則ではなく、何らかの法則の形式だ。
6.321	「因果法則」、これは種名だ。そして、例えば力学に諸最小法則――最小作用の法則のような――が存在するように、物理学には諸因果法則、因果形式の諸法則が存在する。
6.3211	実際、ひとは、何らかの「最小作用の法則」が在るに違いないと、それがどういう内容なのかを正確に把握する前から、予感してきたのだ。（ここでも、例のごとく、アプリオリに確実なのは純粋に論理的な何かであることが判明する。）
6.33	我々は保存法則なるものをアプリオリに信じているのではなくて、或る論理的形式の可能性をアプリオリに把握している。
6.34	根拠律、自然における連続性の原理、自然における最小消費の原理等々のような命題の総ては、科学の文の可能な造形についてのアプリオリな洞察だ。
6.341	例えば、ニュートン力学は世界記述にひとつの統一的形式を提供する。不規則な黒い斑点のある白い平面を考えよう。そこで、我々はこう言う： どんな図柄がそれによって生じようと、当の平面を適当に細かい正方形の網で覆い、そして、それぞれの正方形について、それが白いのか黒いのかを述べることによって、私はその図柄の記述に望むだけ近づくことができる。私はこの方法によって件の平面の記述にひとつの統一的形式を与えおおすだろう。この形式は任意だ。三角形や六角形の目から成る網を同様の成功裡に用いることもできただろうから。三角網による記述の方が簡単にいったということもあり得る。つまり、我々は、件の平面を、細かい正方網よりも粗い三角網を使った方が正確に記述できた（あるいはその逆）等々ということも。別々の網には別々の世界記述のシステムが対応する。力学は、世界記述の文の総ては幾つかの所定の文――力学の諸公理――から或る所定の方法で得られるのでなければならない、と述べることで世界記述の一形式を規定する。それによって、力学は、科学的建築物の建設に資材を供給し、そしてこう言う： どんな建築物を建てるつもりにせよ、それをお前はもっぱらこれだけの資材でもってどうにかしなければならない。 （数のシステムによってあらゆる任意の数を書下すことができるように、ひとは力学のシステムによって物理学のあらゆる任意の文を書下すことができるはずだ。）
6.342	そして、いま、我々には論理と力学の相対的ポジションが見える。（ひとは件の網を例えば三角形と六角形からというように種々の図形から成るようにすることもできただろう。）先に述べられたような図柄が或る適当な形式の網によって記述され得ることは、当の図柄について何ごとも言明しはしない。（そのことはその種の図柄の何れについても当てはまるのだから。）だが、その図柄が特定の細かさをもつ特定の網によって完全に記述され得ること、これは当の図柄を特徴づける。 同様に、世界がニュートン力学によって記述され得ることは、世界について何ごとも言明しはしないが、しかし、世界がかの力学によってこのことがまさに成り立つとおりに記述され得ることは、世界を特徴づける。また、一方の力学によっての方が他方によってよりも世界は簡潔に記述され得るということも、世界についてなにがしかを述べている。
6.343	力学は我々が世界記述に必要とする総ての真な文をひとつのプランに随って構成する企てだ。
6.3431	論理的機構全体を通じて、物理法則全般は世界の対象全般について語るのだ。
6.3432	我々は、力学による世界記述が恒に全く一般的であることを忘れてはならない。力学で話題にされるのは、例えば、特定の諸質点では決してなく、恒に不特定の諸質点ばかりだ。
6.35	我々の図柄における斑点は何れも幾何学的図形ではあるが、もちろん、幾何学はそれらの実際の形や位置については全く何も述べ得ない。件の網は、だが、純粋に幾何学的だ。その総ての属性はアプリオリに特定され得る。 根拠律等々のような法則は網を主題としている。網が記述するものをではない。
6.36	因果法則なるものが在ったならば、その内容はこうかも知れない： 「諸自然法則が存在する」。 だが、もちろん、ひとはそう言うことはできない。それは自ずと明らかになるのだ。
6.361	ヘルツの口吻でひとはこう言うかも知れない： ただ法則通りの聯関だけが思惟可能だ。
6.3611	我々はひとつのプロセスを「時の経過」と較べることなどできない――時の経過は存在しない。ただ何か別のプロセスと（例えばクロノメーターの動きと）較べ得るだけだ。 だから、時間的推移の記述は、もっぱら我々が何か別のプロセスに拠る限りにおいて可能だ。 全く同様のことが空間にも当てはまる。ひとが、例えば、ふたつの（両立しない）出来事について、他方でなく一方が起るべきどんな理由も存在しないのだからどちらも起り得ない、と言うとき、実際に問題になっているのは、どんな非対称性も存在しないならば、ひとはそれらふたつの出来事のうちのひとつを記述することなど全くできないということだ。そして、そのような非対称性が存在する場合、我々はそれを一方が現実のものとなり他方がならないことの理由と解し得る。
6.36111	カント流の右手と左手の問題、それらをひとは重ね合わし得ないという問題は、平面でも、それどころか一次元空間でも存立する。そこでは、a と b のようなふたつの合同な図形でさえ、当の空間の外へ動かされること無く重ね合わされることはあり得ない。 右手と左手は実は全く合同だ。しかし、そのこととひとがそれらを重ね合わし得ないことは何の関わりもない。 右手袋を四次元空間で回転させることができたならば、ひとはそれを左手に着け得ることだろう。
6.362	記述され得ることがらは、また、生じ得る。そして、因果法則によって締め出されるものとされることがらは、記述されもし得ない。
6.363	帰納のプロセスは、我々が自らの経験と調和させ得る最も単純な法則を採用する点に在る。
6.3631	そのプロセスは、だが、どんな論理的根拠づけももたない。ただ何らかの心理的根拠づけをもつだけだ。 最も単純なケースがとにかくまた実際に生じるだろうと信じる根拠など存在しないことは明らかだ。
6.36311	太陽があした昇るだろうというのは仮説であり、それは、我々は太陽が昇ることになるのかどうか判らないということを意味する。
6.37	或ることが生じたということから別の或ることが生じざるを得なくさせるような、そんな強制は存在しない。ただ何らかの論理的必然性だけが存在する。
6.371	いわゆる自然法則全般は自然現象全般の説明だという錯覚が、近代的世界観全体の基礎を成している。
6.372	それで、ひとびとは自然法則全般のもとに、何やら不可侵のもののもとでの如く、立ち尽くしている。古人が神や運命のもとにそうしたように。 そして、どちらも正当性と不当性をともにもってはいる。しかし、新たなシステムのもとでは総てが説明されているかのように見えてしまうのに対して、はっきりとした断絶を認めている点で、古人の方が明晰だ。
6.373	世界は私の意志とは独立している。
6.374	たとえ我々が望むことの総てが生じたとしても、それはやはり謂わば運命の恩寵でしかないだろう。それを保証するような、意志と世界の間の論理的聯関など存在しないのだし、それに、我々は仮定された物理的聯関そのものをまた欲することなどできないだろうから。
6.375	論理的必然性だけが存在するのと同様に、論理的不可能性だけがまた存在する。
6.3751	例えば、ふたつの色が視野の一箇所にともに在ることは不可能、しかも論理的に不可能だ。それは色の論理的構造によって排除されるのだから。 この矛盾が物理学においてどう表わされるか考えてみよう。それは、おおよそこうだ： ひとつの粒子が同時にふたつの速度をもつことはあり得ない、つまり、ひとつの粒子は同時にふたつの場処には在り得ない、つまり、同じ時、色々な場処における諸粒子は同一ではあり得ない。 （ふたつの基本的文の論理積はトートロジーでもコントラディクションでもあり得ないことは明らかだ。視野の一点が同時にふたつの相異なる色をもつという言明はコントラディクションだ。）
6.4	総ての文は対等だ。
6.41	世界の意味は世界の外に在るはずだ。世界においては総ては在るがままに在り、生じるがままに生じる。世界の中には何の価値も存在しない――それに、存在したとしても、それは何の価値ももたないことだろう。 価値をもつ価値なるものが存在するならば、それは総ての生起と相在〔So-Seins〕の外に在るはずだ。総ての生起と相在は偶然的なのだから。 それを非偶然的にするものは、世界の中には在り得ない。在り得たとすれば、そのことはまた偶然的だろうから。 それは世界の外に在るはずだ。
6.42	したがって、倫理の文なども存在し得ない。 文は高次のものを何も表現し得ない。
6.421	倫理は言い表わされ得ないことは明らかだ。 倫理は超越論的だ。 （倫理と美学はひとつのものだ。）
6.422	「お前は ・ ・ ・ すべきだ」という形式の倫理法則を立てる際の最初の考えはこれだ： だが私がそれをしない場合には？ しかし、倫理が通常の意味での罰および賞とは何の関わりもないことは明らかだ。だから、或る行為の諸帰結についてのこの問いは重要ではないはずだ。――少なくとも、そうした帰結は出来事であってはならない。件の問題設定にも何か正当なところはあるはずなのだから。たしかに、或る種の倫理的な罰や倫理的な賞は存在するには違いないが、しかし、それらは当の行為そのもののうちに在るはずだ。 （また、賞が何か好ましいことがらで、罰が好ましくないことがらである必要があることも明らかだ。）
6.423	倫理的なものの担い手としての意志は語られ得ない。 そして、現象としての意志はただ心理学の興味を惹くだけだ。
6.43	善き志なり悪しき志なりが世界を変えるにしても、それは、ただ世界の限界を変え得るだけであり、事実全般を変えることはできない。言語によって表現され得ることがらを変えることはできない。 要するに、世界は、そのときそれによって、そもそも別ものになるはずだ。世界は謂わば全体として減るか増えるかするはずだ。 幸福な者の世界は不幸な者の世界とは別ものだ。
6.431	死の際にさえ、世界は変わらない。終わるのだ。
6.4311	死は生の出来事ではない。死をひとが体験することはない。 ひとが永遠ということを無限の期間ではなく、無時間性と解するならば、現在において生きている者は永遠に生きている。 我々の視野が限り無いのと同様、我々の生は果てし無い。
6.4312	人間の魂の時間的不死性、つまり、魂が死後にも永遠に生き続けることは、到底保証されない。そればかりか、この仮定は、とりわけ、ひとが恒にそれによって叶えようとしていることがらを全く果たさない。そもそも私が永遠に行き続けることによって何か謎が解かれるのか？ それに、そもそもその永遠の生は現在の生と同様に不可解ではないか？ 空間と時間の中の生の謎の解決は、空間と時間の外に位置する。 （解かれるべきは自然科学の問題などではないのだ。）
6.432	世界がどのようであるかは、高次のものには全くどうでもいいことだ。神は自らを世界の中には啓示しない。
6.4321	事実の総てはもっぱら課題に必要とされる。解決にではない。
6.44	世界がどのようであるかではなくて、それが在ることが神秘だ。
6.45	永遠の相のもとの〔sub specie aeterni〕世界の観想は、全体――限定された――としての世界の観想だ。 限定された全体としての世界という感じが神秘だ。
6.5	言い表わし得ない答えについては、ひとは当の問いも言い表わし得ない。 当の謎は存在しない。 そもそも或る問いが立てられ得るならば、それはまた答えられ得る。
6.51	懐疑論は、それが問われ得ないことがらを疑おうとするのならば、論駁不能なのではなく、明らかにナンセンスだ。 というのは、懐疑は何らかの問いが存立する場合にもっぱら存立し得て、問いというものは何らかの答えが存立する場合に、そしてその答えは何ごとかが述べられ得る場合に、もっぱら存立し得るからだ。
6.52	我々は、たとえ総ての可能な科学的な問いが解答されても、我々の生の問題は全く触れられないままだと感じる。もちろん、そのときにはもう何の問いも残ってはいないのであり、そして、このことこそが答えだ。
6.521	生の問題の消失によって、ひとは当の問題の解決に気づく。 （或る種の人間、彼らにおいて生の意味が長い懐疑の末に明らかとなったような、そんなひとびとが、当の意味がどんな点に在るのかを述べることができなかったのは、このことに由るのではないか。）
6.522	それでも、言い表わし得ないことがらは存在する。このことは自ずと明らかになる。それが神秘だ。
6.53	哲学の正しい方法は本来こうだろう： 述べられ得ること以外は、したがって、自然科学の諸文以外は――したがって、哲学に何の関わりもないこと以外は――何も述べないこと、そして、他人が何か形而上学的なことを言おうとしたら、彼がそうした文における或る種の記号に何の意義も与えてはいなかったことを明らかにしてみせること。この方法はその者には満足がいかないことだろう――彼は我々が彼に哲学を教えているという感じをもたないことだろう――が、しかし、これが唯一厳正な方法だろう。
6.54	私の諸文は、私を理解する者が、それらを通じて――それらによって――それらの上へと昇ったあげく、それらがナンセンスだと認識すること、そのことを通じて解明する。（彼は、謂わば梯子を登ってしまってから、それを抛棄しなければならない。） 彼はこれらの文をのりこえなければならならず、そうすれば、彼は世界を正しく見て取る。
7	語り得ないことがらについては、ひとは黙らなければならない。

〔翻訳： 大熊康彦〕

---

論理哲学論考　1-7